©PaperWeekly 原创 · 作者 | Yunpeng Tai
主页 | https://yunpengtai.top/
在机器学习中,我们通常会面临一个问题:给定一个集合 ,从中寻找 个样本构成子集 ,尽量使得子集的质量高同时多样性好。比如在推荐系统中,我们就希望给用户推荐的东西尽可能的有质量,同时具有差异性。
而使得采样的子集尽可能具备多样性便是行列式点过程(Determinantal Point Process)大展身手的地方,俗称 DPP。

边缘分布
首先引入 DPP 的边缘分布定义,当我们某次采样出子集,「包括」 的概率:

是核矩阵(Kernel Matrix),即:
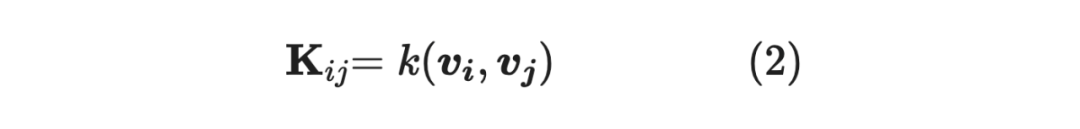
是由 中元素构成的子矩阵,举个例子,假如 ,那么:
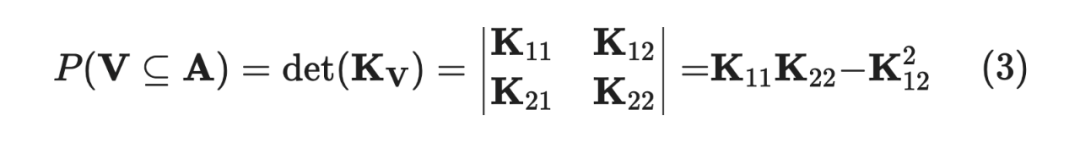
当 越大,则 同时出现在 的概率就越小,从这个角度想,核函数应该是呈现出某种相似性。
从正定性出发,严格的定义如下是:
举个例子:
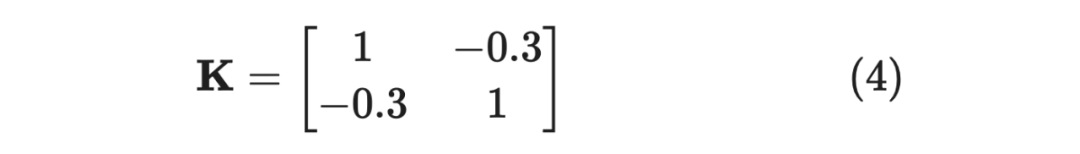
其特征值为 ,不满足 ,即不是半正定矩阵。

L-Ensemble
然而,上面边缘定义只是告诉我们采样时,某个子集被「包括」的概率,并非就是这个子集,而这个问题可以通过 L-Ensemble 去解
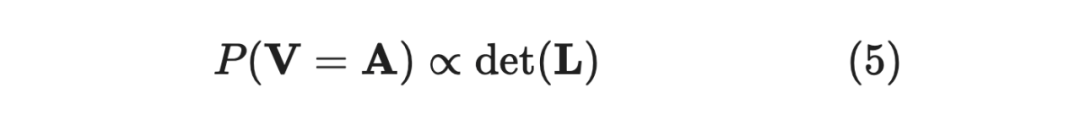
这里的 省略了下标,跟上面的 一样,是跟 元素相关的子矩阵。 矩阵的核函数是内积是 ,。
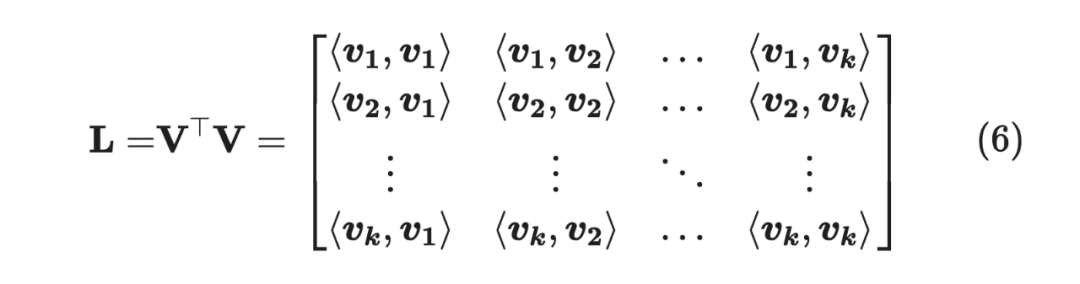
注意,这里指的不是概率,而是说概率「正比于」 矩阵的行列式,那么如何计算概率呢?也就是说我们得计算一个归一化常数(normalization constant),可以类比抛硬币,我们得去求总的抛起次数,除以它才能得到概率。
引入下述定理:
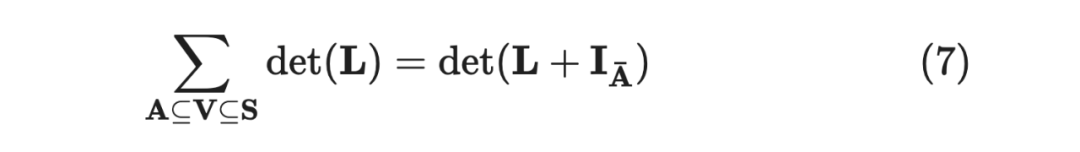
其中 是将单位矩阵中与 相关元素全部置零,举个例子,当 时:
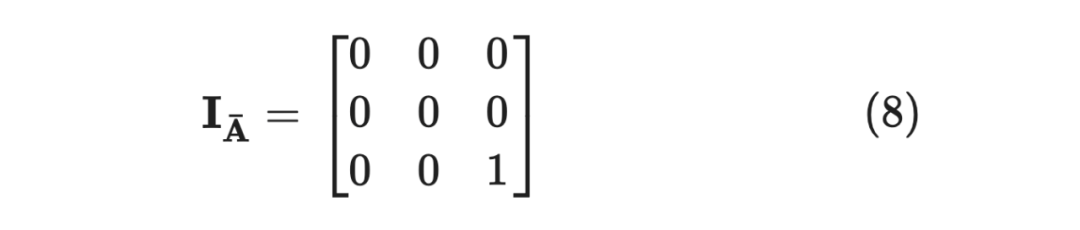
那么如何求归一化常数呢,即将 ,当 为空集时,便包括了所有的情况,即:
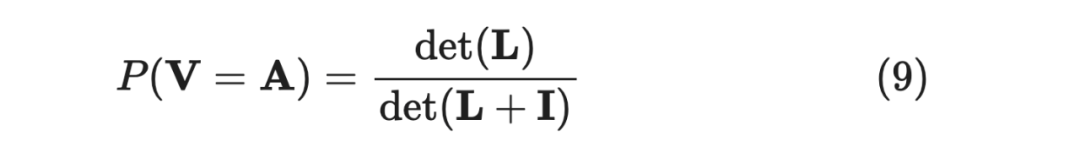
另外,L-Emsemble 的 对应关系如下:
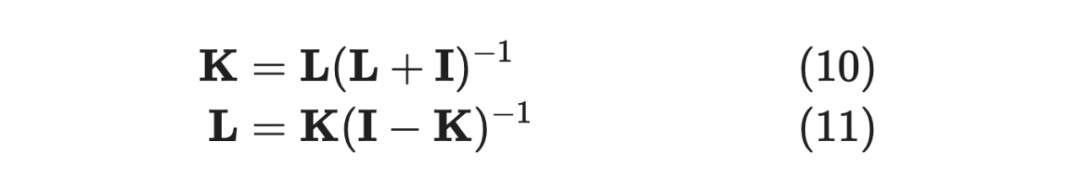

直观解释
那么,行列式与多样性的直观解释是什么呢?
多样性和相似性的意思正好相反,通常我们会定义相似性为两个向量之间做点积,即为 ,直观上看,两向量夹角的余弦值 越大,相似性越高,反过来看,当 最小即为两者相似性最差,多样性最好。显然,当两向量正交时多样性最好。
那么,对于一个子集 而言,该如何定义它的多样性呢?不难想出,可以通过线性无关向量的数量来定义,若两两都互不线性相关,此时的子集的多样性是最好的。直观上可以转换为构成的超平行体的体积,下方为 时的示意图。
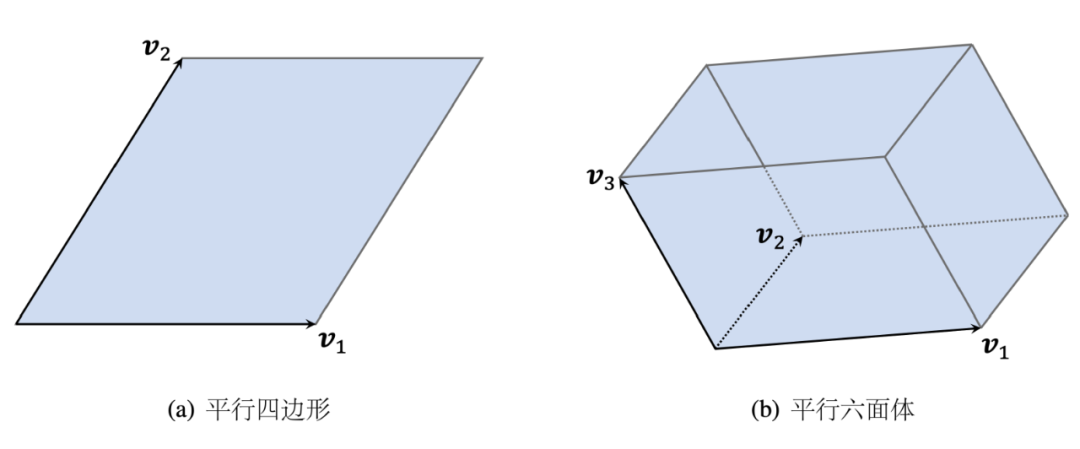
为什么呢?可以拿平行六面体为例,若其中一个向量与其他向量线性相关,那么则会坍缩成一个平面,构不成平行六面体

只有当所有向量两两都线性无关时,构成的超平行体体积最大,即多样性最好。
而行列式可以表示体积,下式中 代表体积(volume),此时 , 为方阵
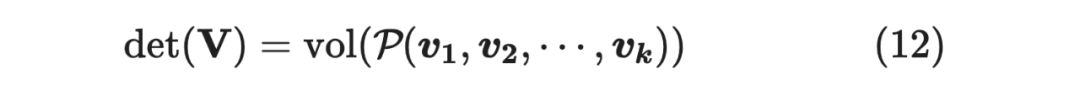
也就是说,我们可以通过行列式的大小来定义多样性。
那么, 的行列式是否也跟体积有关呢?答案是肯定的:
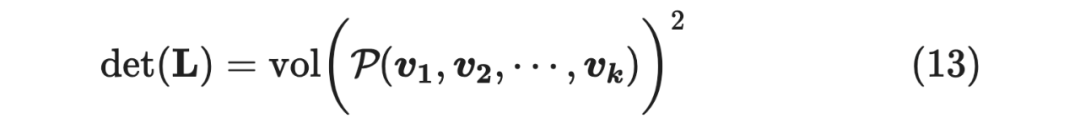
接下来证明这一结论:
由于 ,因为 维空间至多存在 个两两线性无关的向量,那么肯定存在一个 维子空间 ,存在正交矩阵 ,对向量 进行旋转,使得 都落在子空间 上。不妨设 的基底是前 个标准正交基,那么:

, 一共有 个,因为用 的基底向量表示,后面只能为,将 当作 的列,就有:
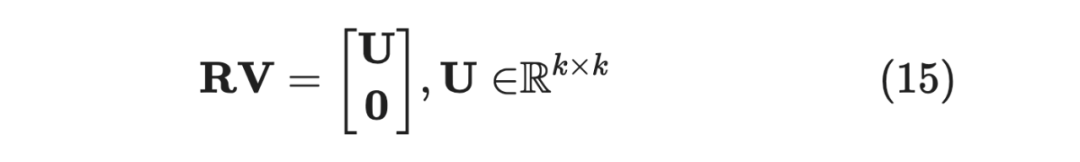
显然, 与 两者体积相等。
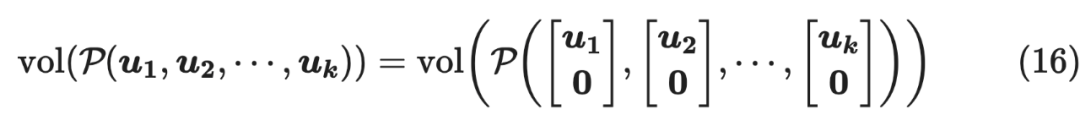
那么:
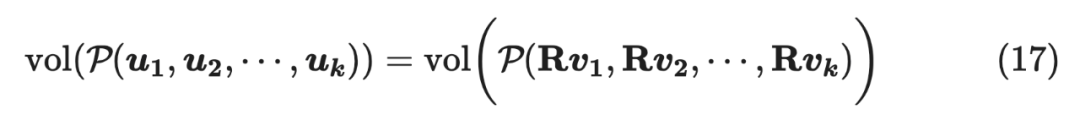
由于对超平面体进行旋转不改变其体积(注意,这里是旋转而不是一般的线性变换,一般的线性变换不具备该性质)。
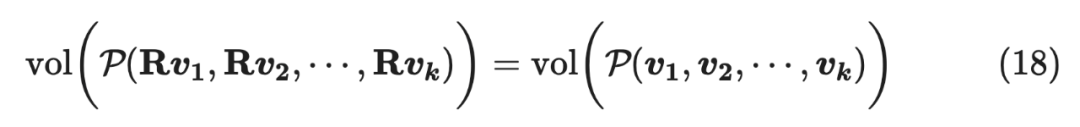
那么:
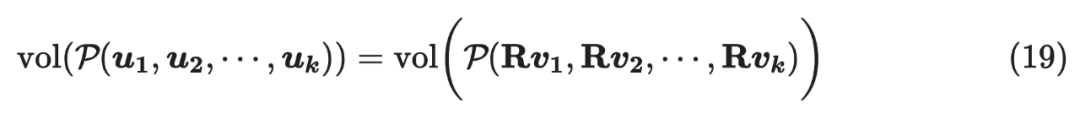
又因为 正交矩阵,即 ,那么:

所以:
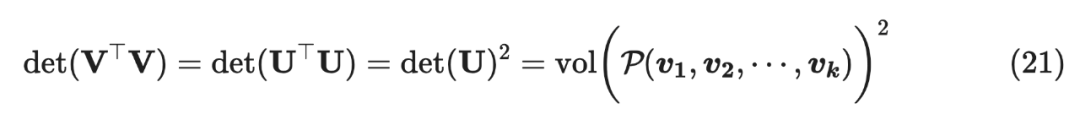
从 L-Emsemble 角度看,被采样的概率正比于构成的超平面体的体积,即两两之间线性无关更容易被采样出。

Demo
接下来我们用例子来看一下是否 DPP 能够采样出更有多样性的子集。
from torch import det, eye
from transformers import set_seed
from transformers import BertModel, BertTokenizer
set_seed(42)
pretrain_path = "fabriceyhc/bert-base-uncased-imdb"
model = BertModel.from_pretrained(pretrain_path).cuda()
tk = BertTokenizer.from_pretrained(pretrain_path)
input_text = [
"I am happy because the weather is extremely good!",
"I hate the bad weather",
"The weather is extremely good!",
]
inputs = tk(input_text, max_length=128, return_tensors="pt", truncation=True, padding=True)
inputs = {k: v.cuda() for k, v in inputs.items()}
outputs = model(**inputs).pooler_output.T
vtv = outputs.T @ outputs
group_12 = vtv[:2][:, [0, 1]]
I = eye(2).cuda()
p_12 = det(group_12) / det(group_12 + I)
group_13 = vtv[[0, 2]][:, [0, 2]]
p_13 = det(group_13) / det(group_13 + I)
print('采样到第一个和第二个的概率:%f'%p_12)
print('采样到第一个和第三个的概率:%f'%p_13)
# 采样到第一个和第二个的概率:0.983567
# 采样到第一个和第三个的概率:0.923823然而,对于一个大小为 的集合,一共有 种组合,如何快速地进行 DPP 的计算以及如何最快找到大小为 的多样性最大的子集是比较困难的,留给下文。

问题
先规定一些术语:记选中元素构成的集合为 ,未选中构成的元素记为 , 是核矩阵(核函数是内积), 是由集合 的元素构成的子矩阵。
在上文中我们提到在大小为 的集合里去挑选 个物品构成集合 ,使得 最大便是我们的目标,然而,怎么去里面挑选 却是 NP-Hard 问题,为此,Chen et al., 2018 提出了一篇比较巧妙的贪婪算法作为近似解,并且整个算法的复杂仅有 。

暴力求解
我们人为规定了要选择 个,这相当于是一种前验分布,那么 k-DPP 其实就是最大化后验概率(MAP)的一种,每一步的目标就是选择会让新矩阵的行列式变得最大的元素。
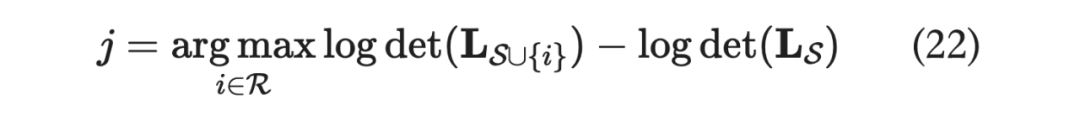
对于一个 的方阵而言,求它的行列式需要 (每一轮消元的复杂度是 ,而要进行 轮消元)。
这里的话,每次要对 所有的元素求一次行列式,而行列式的为 ,同时需要选 个,复杂度变为了 ,即为 ,暴力求解的话复杂度很大,此时原作者便提出了利用 Cholesky 分解的方式来进行求解,巧妙地将复杂度降到了 。

Cholesky分解
是对称半正定矩阵,证明如下:
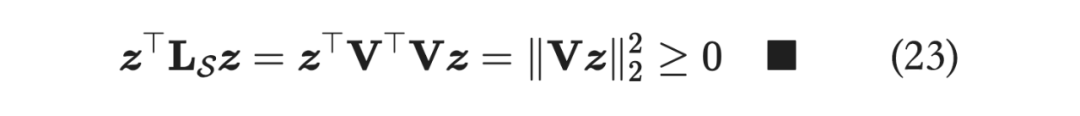
那么 存在 Cholesky 分解,即 ,这里的 是大小为 的下三角矩阵, 比 多了一行和一列,即为:
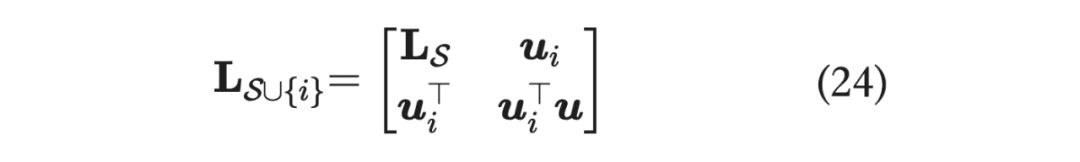
而这里默认每个向量是经过归一化的,即 ,那么 的 Cholesky 分解即为下式,其中 :
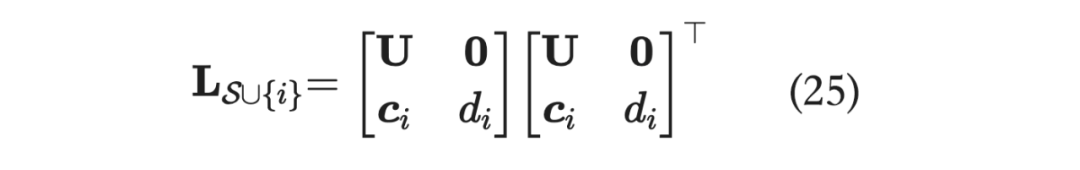
结合上面两式:

可得:
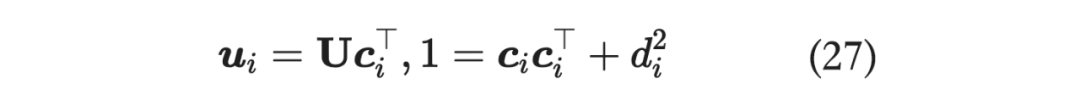
那么:
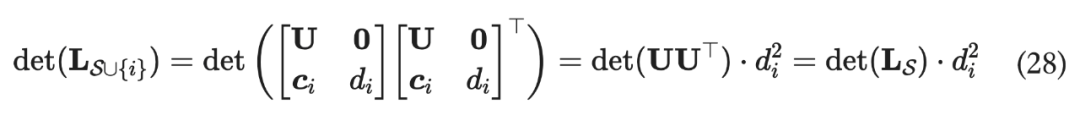
这样我们一开始的优化目标就可以简化为:
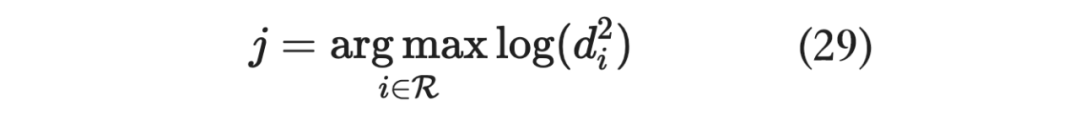
接下来,当我们得到 时,便可以算出 ,那么添加 之后的新集合 的 Cholesky 分解便可以求得:
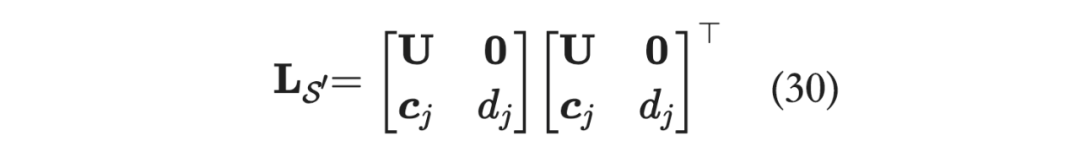

增量更新
接下来便是重头戏,这一轮我们已经得到了最好的 了,下一轮我们怎么求出最大的 呢?
可以利用之前求出的 来获取当前的 ,这便是论文的核心:增量更新
在我们选择了 后, 多了一个元素,不妨记 ,回忆上面的式子:
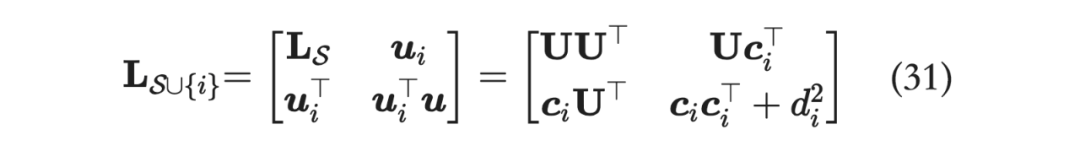
也就是说,其中 就是第 个元素与集合 对应向量做内积的结果。
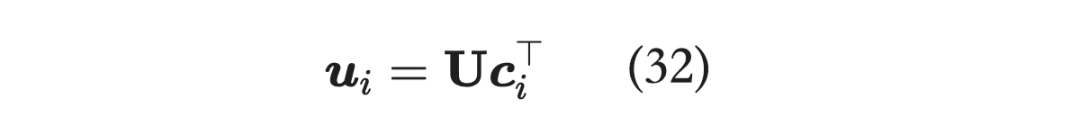
那么,类比一下, 是 的 Cholesky 分解。
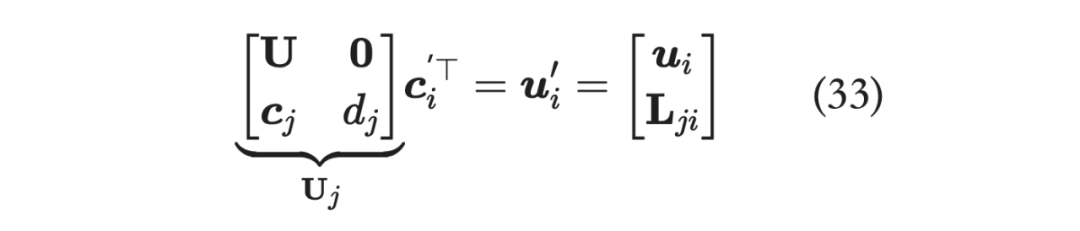
继而:
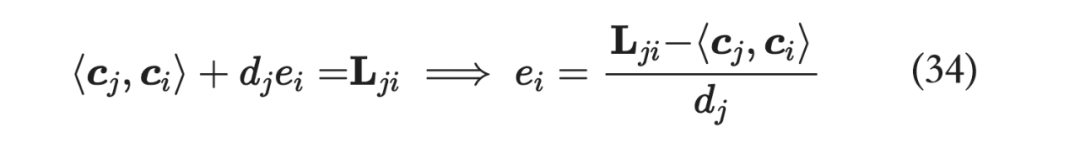
求出 之后,我们便可以求出 :
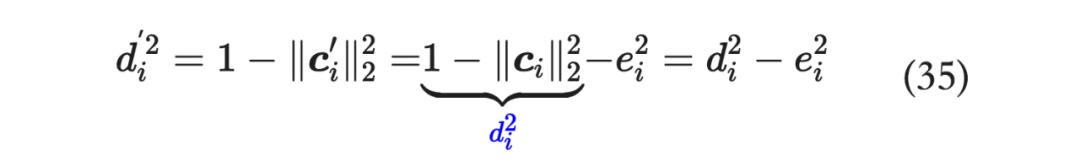

流程

那我们来分析一下复杂度,每选一个 需要进行 次操作,而 ,也就是 ,得进行 次迭代,那么总的复杂度即为 ,由 降到 ,是不错的进步。

代码
熟悉了整个流程之后,代码想必也是呼之欲出了。
import math
import numpy as np
def fast_map_dpp(kernel_matrix, max_length):
cis = np.zeros((max_length, kernel_matrix.shape[0]))
di2s = np.copy(np.diag(kernel_matrix))
selected = np.argmax(di2s)
selected_items = [selected]
while len(selected_items) < max_length:
idx = len(selected_items) - 1
ci_optimal = cis[:idx, selected]
di_optimal = math.sqrt(di2s[selected])
elements = kernel_matrix[selected, :]
eis = (elements - ci_optimal @ cis[:idx, :]) / di_optimal
cis[idx, :] = eis
di2s -= np.square(eis)
di2s[selected] = -np.inf
selected = np.argmax(di2s)
selected_items.append(selected)
return selected_items这里实现比较有趣的点就是,尽管伪代码中是 ,这里其实是全部算了,但他对已选的进行了后处理,置之为 。
接下来我们实操一下,从句子对匹配 BQ Corpus(Bank Question Corpus)拿出一条来看一下效果,首先是将其用预训练模型转换为表征向量,接着进行归一化操作,为了更好地看出 DPP 的效果,我们先用最大化内积来召回 50 个样本,再用 DPP 从这里召回 10 个具有多样性的样本:
原句:我现在申请微粒货?
['我现在申请微粒货?', '申请微贷粒', '申请微贷粒', '我想申请微粒贷', '可以么想申请微粒贷', '微粒貸申请', '微粒貸申请', '如何申请微粒', '我现在需要申请', '我可以申请微粒贷吗', '怎么申请微粒货', '微粒貸申请', '如何申请微粒', '我可以申请微粒贷吗', '什么情况下才能申请微粒', '我要求申请', '开通微粒货', '开通微粒貨', '开通微粒货', '可以申请开通吗', '开通微粒货', '开通微粒货', '怎么申请微粒货', '申请贷款', '如何申请微粒贷', '怎么申请微粒货', '开通微粒貨', '如何申请微粒', '想办理微粒贷业务', '申请贷款', '可以申请开通吗', '我要微粒贷', '我要微粒贷', '可以么想申请微粒贷', '开通微米粒', '想开通', '我要微粒贷', '如何申请微粒', '想开通', '开通微粒貨', '开通粒微贷', '何时才能申请啊', '现在想获取资格', '怎么申请微粒货', '开通申请', '开通', '开通', '你好我申请借款', '开通微']可以看到有不少重复且意思一样的样本:
接着看 DPP 的效果:
['我现在申请微粒货?', '开通', '何时才能申请啊', '怎么申请微粒货', '你好我申请借款', '现在想获取资格', '我可以申请微粒贷吗', '我要微粒贷', '微粒貸申请', '什么情况下才能申请微粒']可以发现里面没有重复的情况,而且语义具备多样性,而值得注意的是,此时就有一些和我们的原句意思不匹配的情况,在应用时可以自定义新的 kernel,让它同时注意相似性和多样性;或者可以对 DPP 的样本进行后处理等。

Sliding Window
当 相当大的时候,就会有相似的样本开始出现,即超平行体会开始坍缩,不妨我们将 缩小成一个滑动窗口 ,我们仅仅需要保证窗口内的样本具备多样性即可,即:
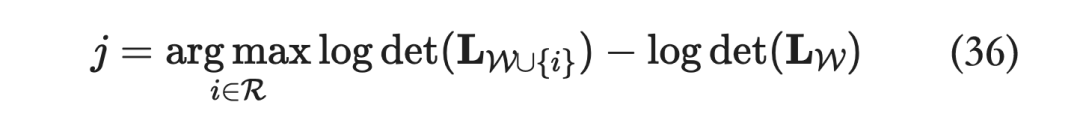
推荐系统中有短序推荐(Short Sequence Recommendation)的说法,推荐的时候只考虑用户短期内的一些行为,而长序推荐会考虑一个较长时间跨度来进行推荐。
Window size 的选择也是比较重要的,不妨看一些 demo:
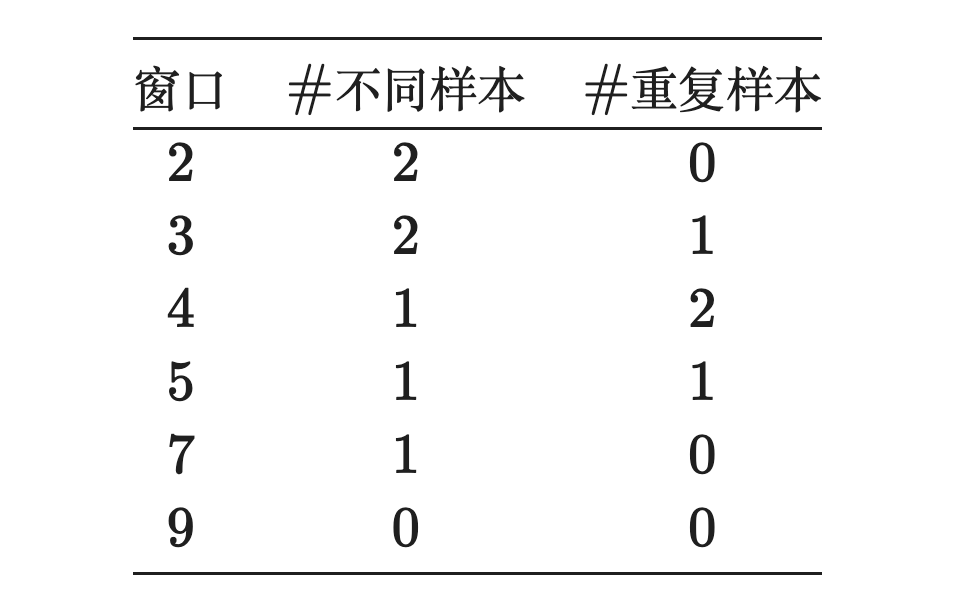
如果我们的目的是为了通过 Sliding Window 获取与直接 DPP 召回不一样的结果,窗口的大小要适当地小一些,然而小了导致看的范围小了,很有可能最后结果出现重复的情况,最好是将窗口设置到召回样本数目的 。
同时,为了防止样本重复,可以多召回一些,比较直觉的做法可以再加上一个 window 的大小,然后去重:
w/o window
['开通', '怎么申请微粒货', '何时才能申请啊', '现在想获取资格', '我要微粒贷', '微粒貸申请', '我可以申请微粒贷吗', '什么情况下才能申请微粒', '你好我申请借款', '我现在申请微粒货?']w/ window
['开通', '开通申请', '怎么申请微粒货', '何时才能申请啊', '现在想获取资格', '我要微粒贷', '我可以申请微粒贷吗', '可以申请开通吗', '如何申请微粒', '我现在申请微粒货?']可以看到会有 3 个不一样的样本,还是比较有效的。
更多阅读




#投 稿 通 道#
让你的文字被更多人看到
如何才能让更多的优质内容以更短路径到达读者群体,缩短读者寻找优质内容的成本呢?答案就是:你不认识的人。
总有一些你不认识的人,知道你想知道的东西。PaperWeekly 或许可以成为一座桥梁,促使不同背景、不同方向的学者和学术灵感相互碰撞,迸发出更多的可能性。
PaperWeekly 鼓励高校实验室或个人,在我们的平台上分享各类优质内容,可以是最新论文解读,也可以是学术热点剖析、科研心得或竞赛经验讲解等。我们的目的只有一个,让知识真正流动起来。
📝 稿件基本要求:
• 文章确系个人原创作品,未曾在公开渠道发表,如为其他平台已发表或待发表的文章,请明确标注
• 稿件建议以 markdown 格式撰写,文中配图以附件形式发送,要求图片清晰,无版权问题
• PaperWeekly 尊重原作者署名权,并将为每篇被采纳的原创首发稿件,提供业内具有竞争力稿酬,具体依据文章阅读量和文章质量阶梯制结算
📬 投稿通道:
• 投稿邮箱:hr@paperweekly.site
• 来稿请备注即时联系方式(微信),以便我们在稿件选用的第一时间联系作者
• 您也可以直接添加小编微信(pwbot02)快速投稿,备注:姓名-投稿

△长按添加PaperWeekly小编
🔍
现在,在「知乎」也能找到我们了
进入知乎首页搜索「PaperWeekly」
点击「关注」订阅我们的专栏吧
·
·