文章目录

树
- 树定义
- 专业术语
- 树分类
二叉树
- 分类
- 存储
- - 连续存储（完全二叉树）
  - 链式存储
  - 一般树的存储
  - 森林的存储
- 线索二叉树
- 哈夫曼树
- - 构造步骤
- 遍历
- - 先序遍历
  - 中序遍历
  - 后续遍历
- 链式二叉树遍历具体代码
- 已知两种遍历序列求原始二叉树
- - 已知先序和中序求后序
  - 已知中序和后序求先序
  - 已知先序和后序求中序
树的应用

树

树定义

像这种有层次关系进行存储的，就是一棵树，是非线性结构。
在这里插入图片描述
以递归的方式进行定义。

专业定义：

有且只有一个称为根的节点。
有若干个互不相交的子树，这些子树本身也是一棵树。

通俗定义：

树是由节点和边组成。
每一个节点节点只有一个父节点但可以有多个子节点。
有一个节点例外，该节点没有父节点，此节点称为根节点。

专业术语

节点：就是一个个的圈。
父节点：和当前节点上一个紧挨着的节点。
子节点：父节点下连着的子节点。
子孙：父节点下的所有节点。
深度：从根节点到最底层的层数称为深度。
叶子节点：没有子节点的节点。
非终端节点：实际上就是非叶子节点，有子节点的节点。
根节点：看有没有子节点。
度：子节点的个数称为度。

树分类

一般树：任意一个节点的子节点的个数都不受限制
二叉树：任意一个节点的子节点个数最多两个，且子节点的位置不可更改。
森林：有互不相交的，一般的树合在一起，就是森林。

二叉树

存储

连续存储（完全二叉树）

要把一颗一般的二叉树以数组方式存储的话，必须先把这个一般的二叉树转化为完全二叉树。

eg:
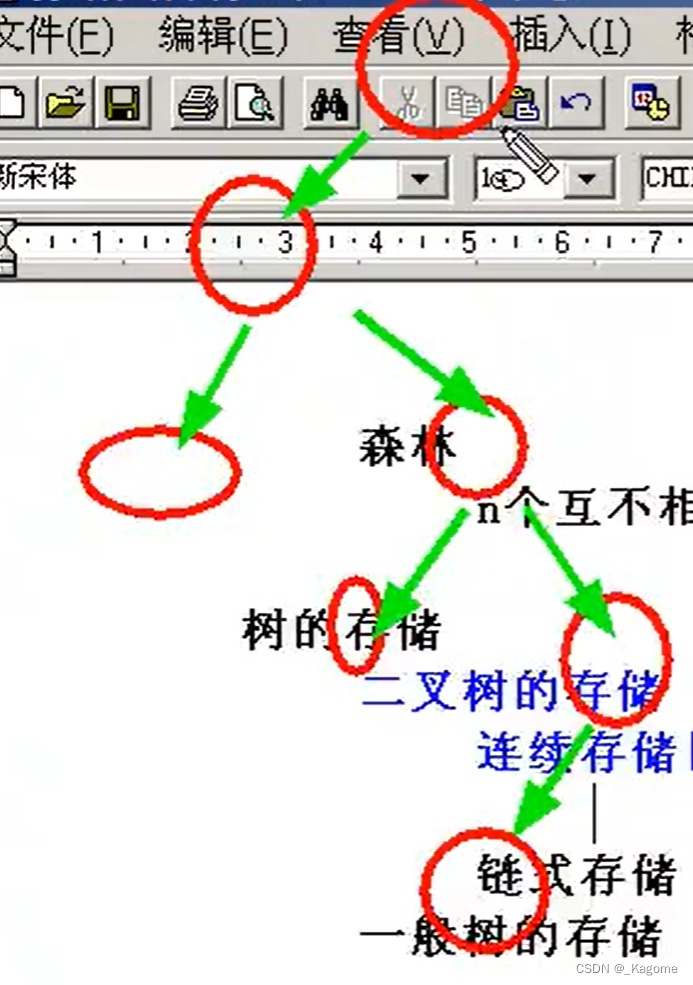
在这里插入图片描述
首先这不是一个完全二叉树，因为完全二叉树先是一个满的二叉树，后来再在最底一层砍。所以要使用连续存储就必须先把这个二叉树变成完全二叉树。

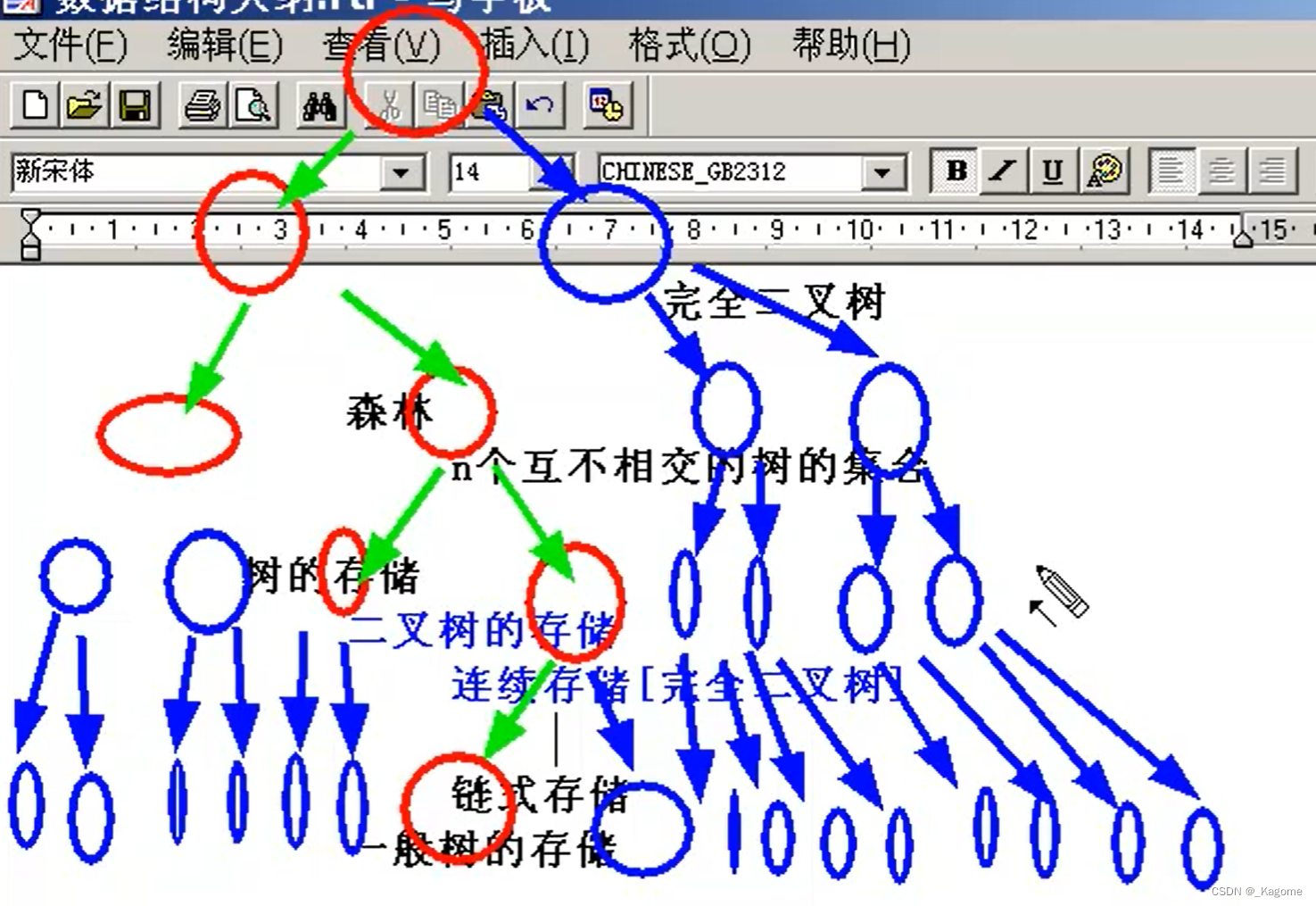
在这里插入图片描述
先变成满二叉树，再把最底层的最右边得到删掉，就成了完全二叉树。

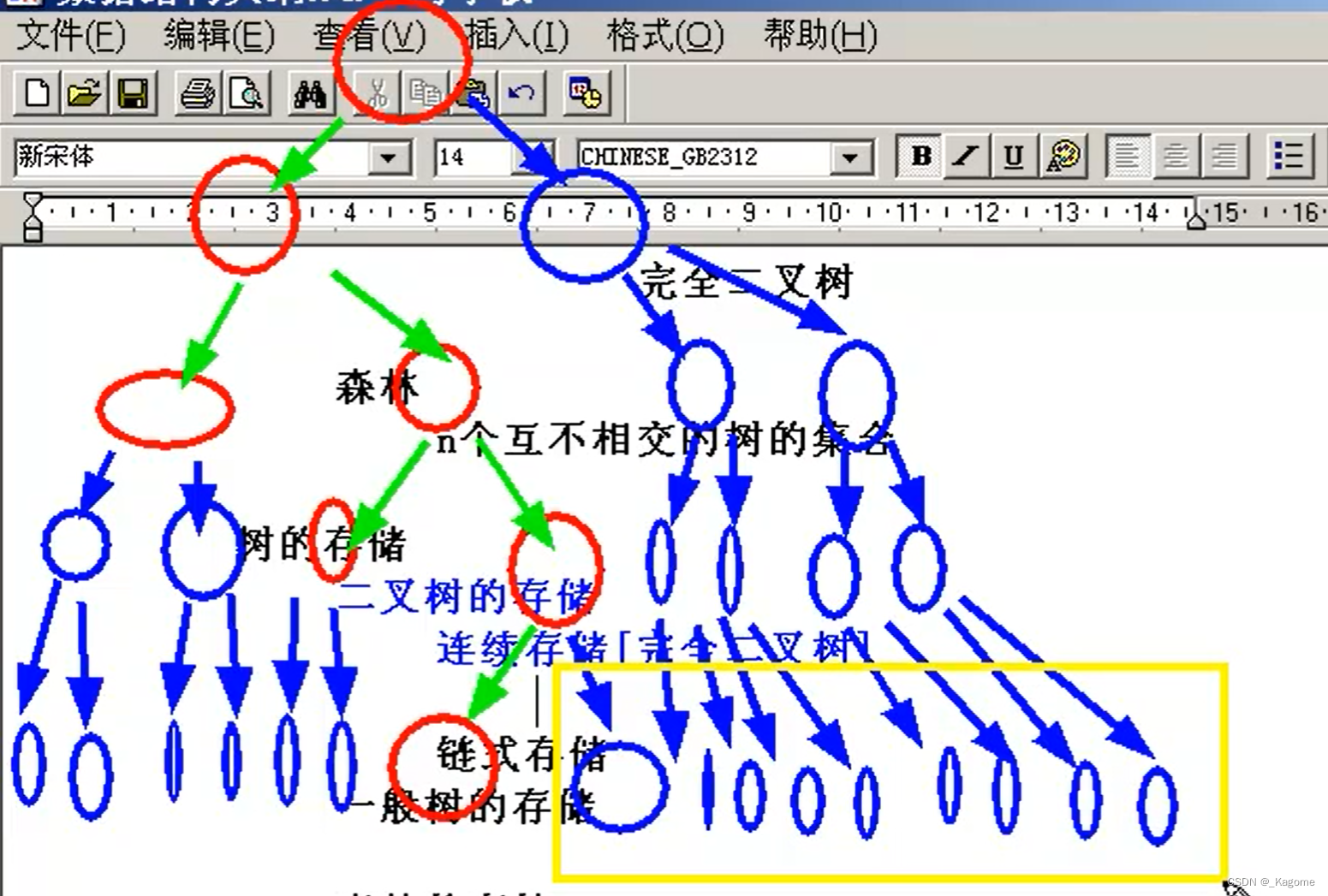
黄色线框的可以不保存。（先转化成满二叉树，再把最后一层最右边开始的点删掉，就是完全二叉树）红色的是有效节点，别人是无法通过零散的红色有效节点还原二叉树的本来面目的。（排序通过先中后进行排序。）
树是非线性的，将非线性的数转换成线性结构的，结果是不知道的。
数组只能以完全二叉树的方式进行存储，即不能只存放有效节点，因为通过先中后进行排序后，还原不了其本来的面目。所以把所有点都存进去，才好还原。

优点：查找某个节点的父节点和子节点很快。
缺点：耗用内存空间过大。

链式存储

通过指针域弄成一个连续的存储。

一般树的存储

双亲表示法：求父节点很方便，因为跟的是下标。
孩子表示法：求子节点方便，跟着的是子节点。
双亲孩子表示法：有链表，有数组，有下标，指针域，求父节点与子节点都很方便，就是代码复杂。
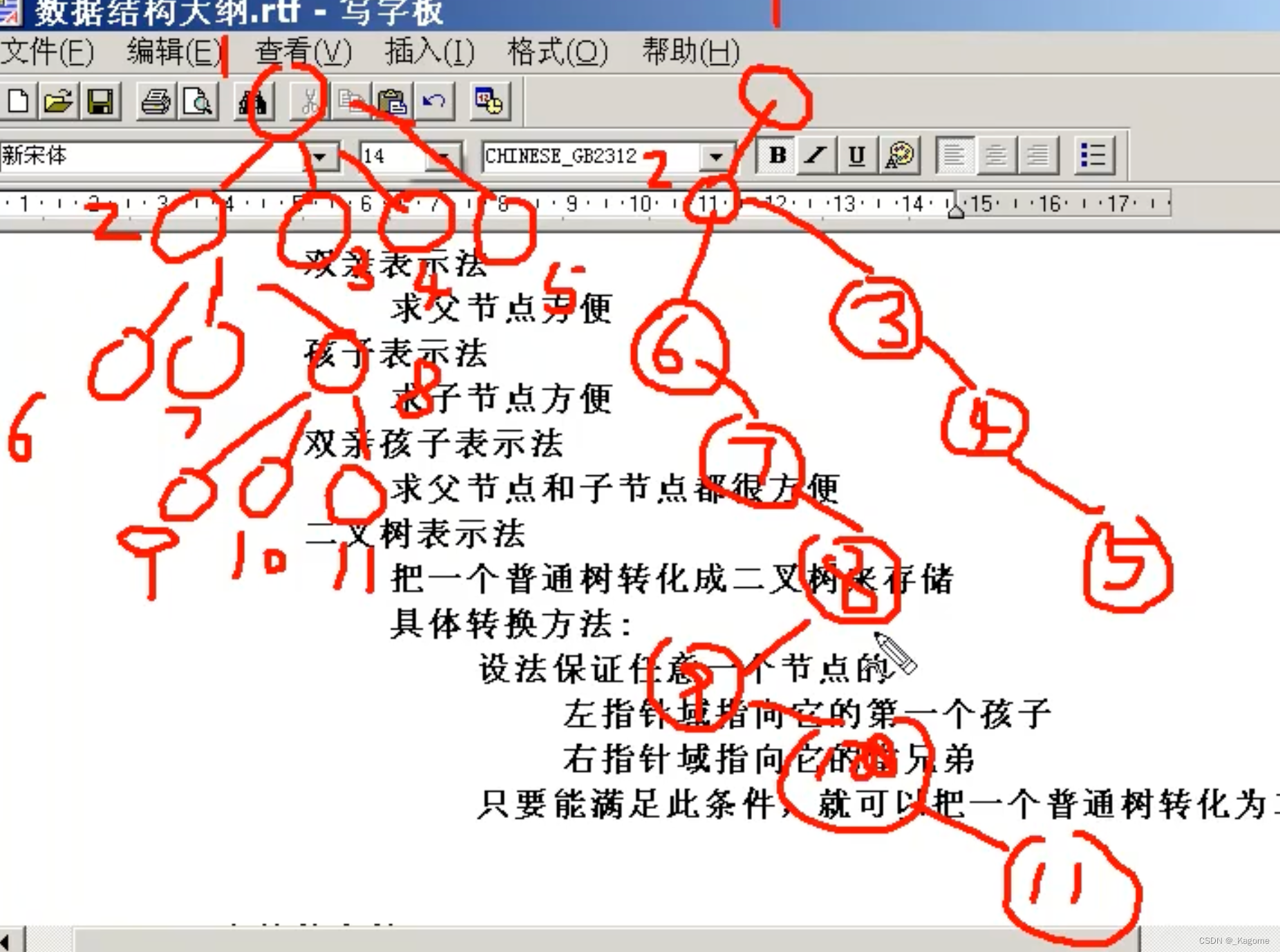
二叉树表示法：把一个普通树转化成二叉树来存储，具体转换方法是，设法保证任意一个节点左指针域指向它的第一个孩子，右指针域指向它的下一个兄弟节点，只要能满足此条件，就能把一个普通的数转化为二叉树。（转化时，只有左边的孩子，右边都是与孩子并列的兄弟，即一个普通的数转化为二叉树就没有右子树。例如下方的2,3,4,5，真正是孩子的只有2，然后3,4,5都是与其并列的项，排在右边。3也没有左兄弟，所以把4排在右边，5就同理了。）
eg如下，将一个普通的树转化为二叉树。

森林的存储

几个树互不相交，就组成了一个森林。
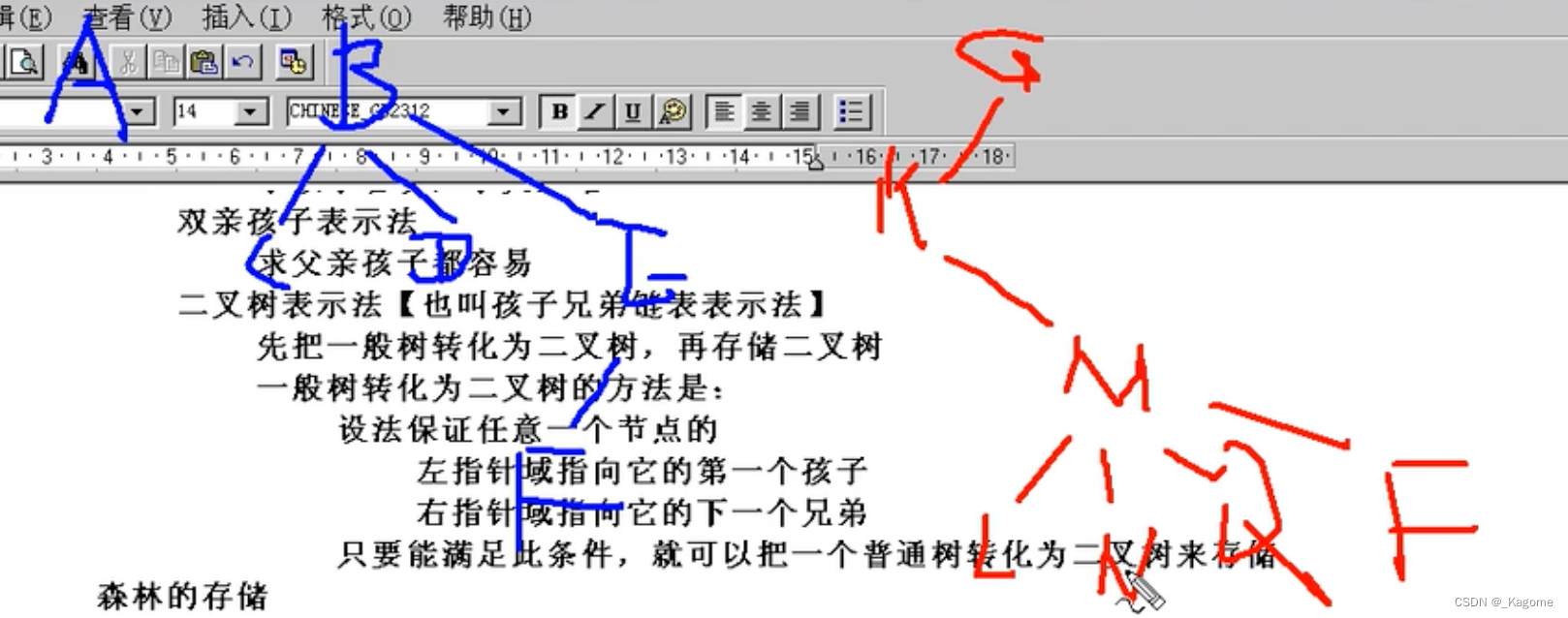
在这里插入图片描述
先把森林转化为一个二叉树，再进行存储。而森林的二叉树存储规则为：把B当A的兄弟，把G当B的兄弟。

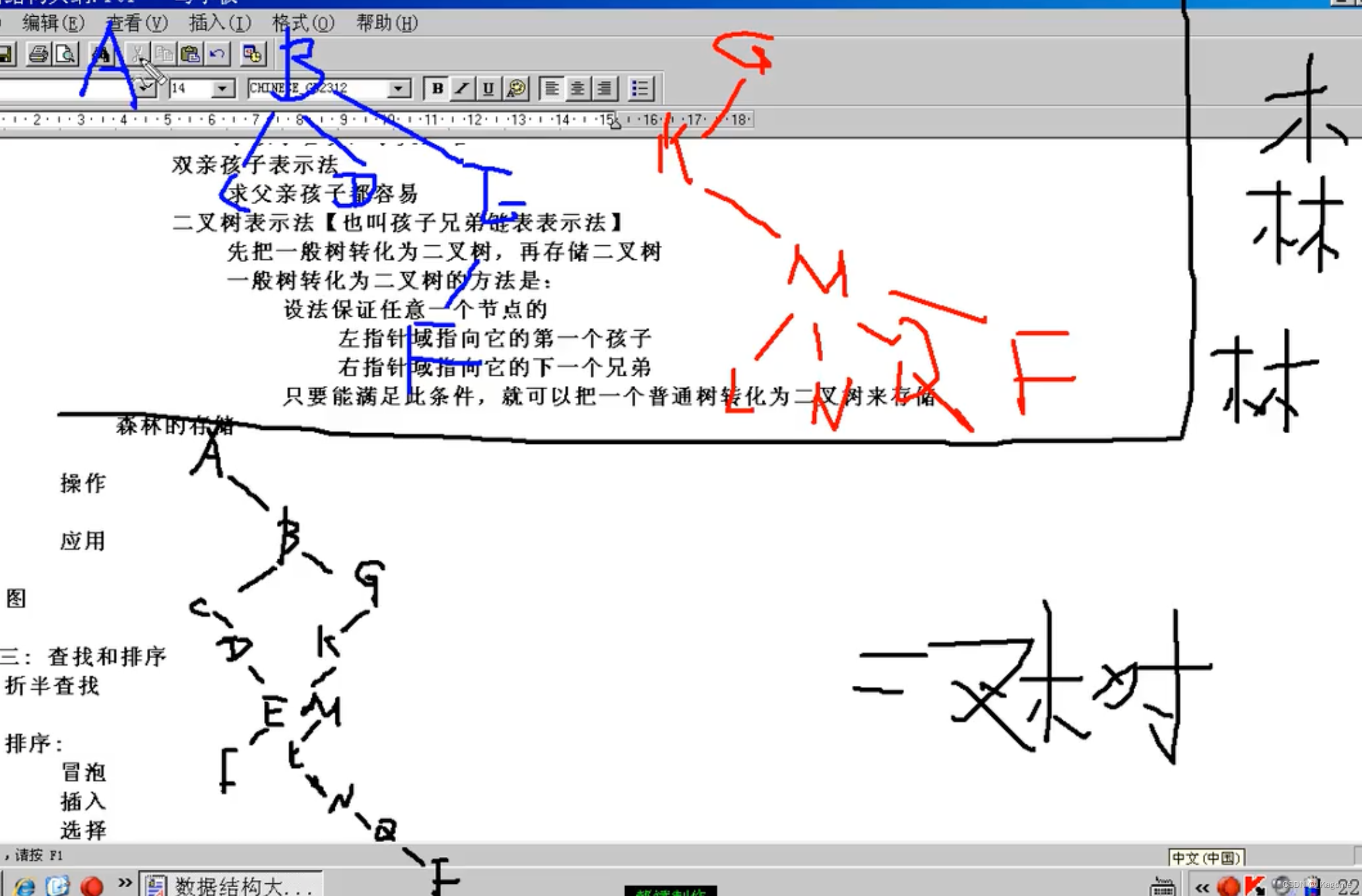
森林转成二叉树的步骤与之前一般树转化为二叉树也是一致的。

线索二叉树

当用二叉链表作为二叉树的存储结构时，可以很方便地找到某个结点的左右孩子；但一般情况下，无法直接找到该结点在某种遍历序列中的前驱和后继结点。
在这里插入图片描述
因为还剩下了n+1个指针域，将其利用起来，存储前驱后继指针的地址，称此为线索。

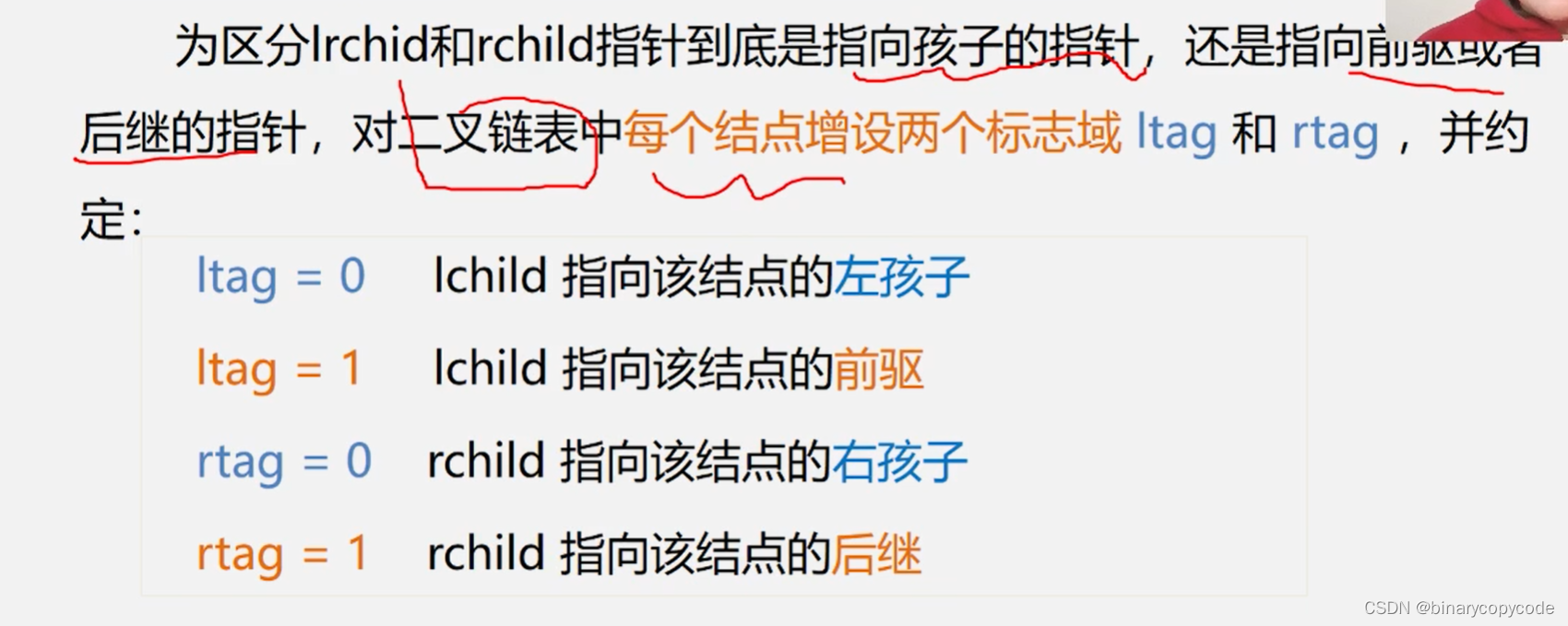
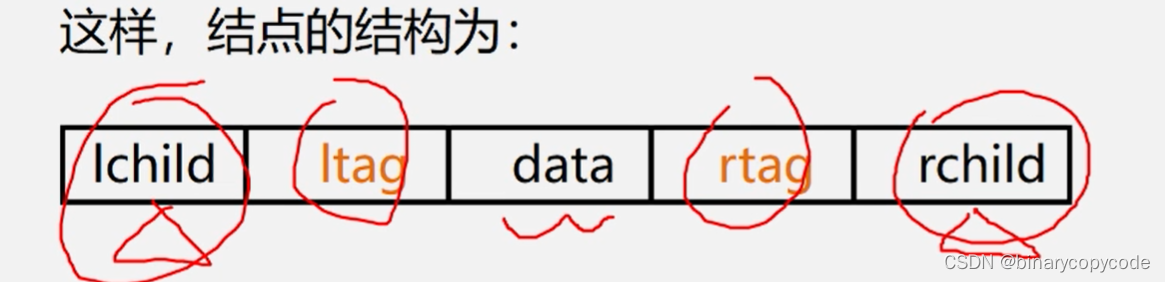
可以用ltag与rtag的方式来区分是否为孩子还是线索。（左孩子与前驱，右孩子与后继）

//线索二叉树的结点结构
typedef struct BiThrNode{
	int data;
	int ltag, rtag;
	struct BiThrNode *lchild, rchild;
}BiThrNode, *BiThrTree;

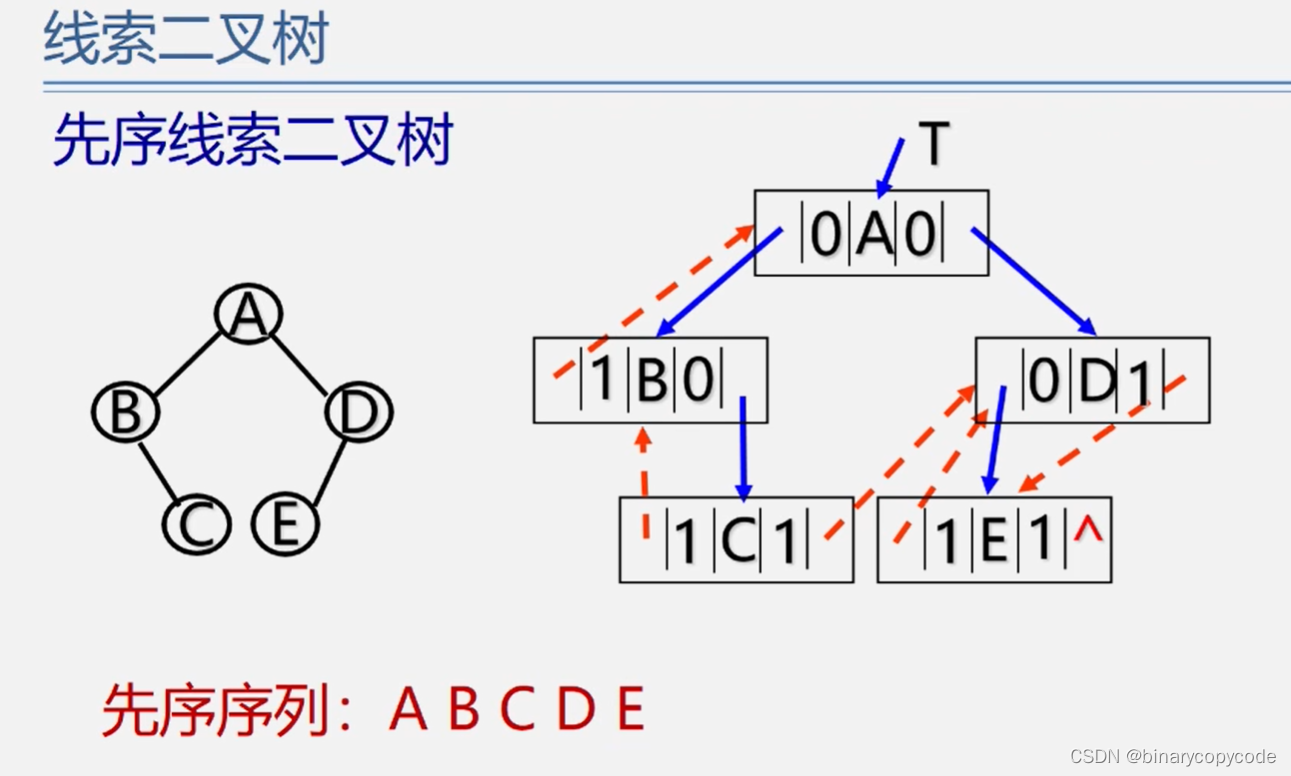
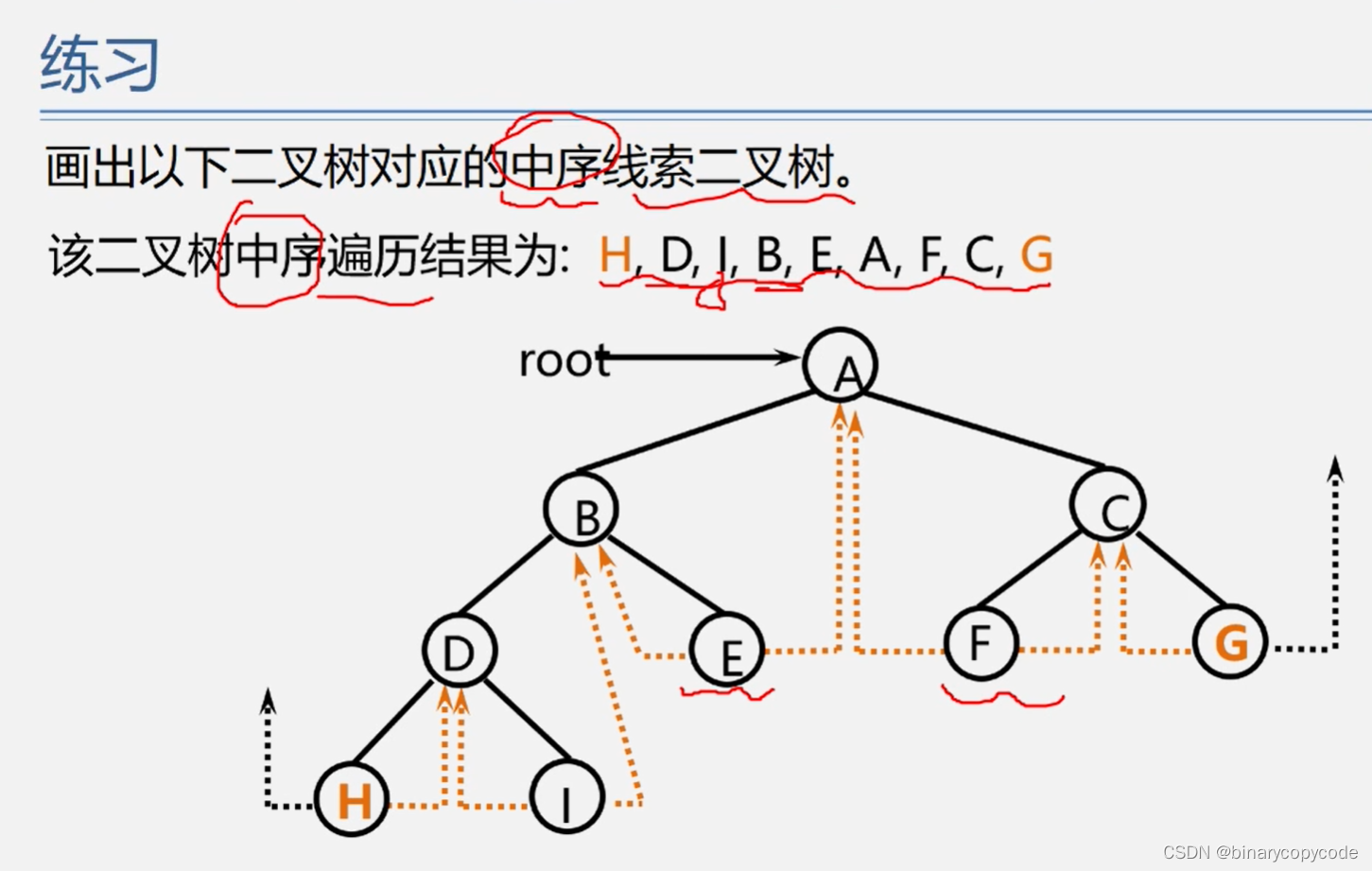
在这里插入图片描述

因为首尾还有两个指针域悬空，可以增加一个头结点，让其指向头结点。

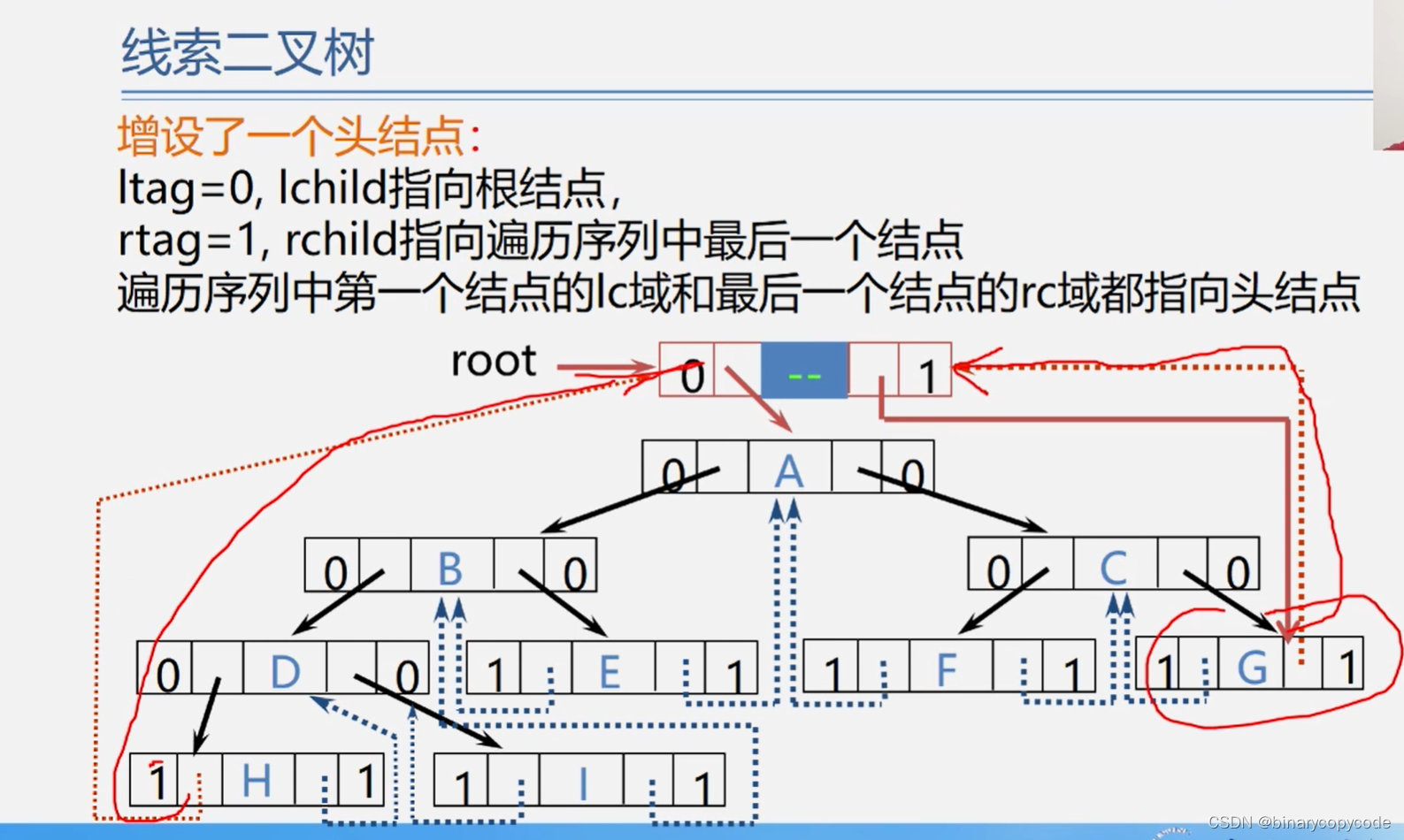
哈夫曼树

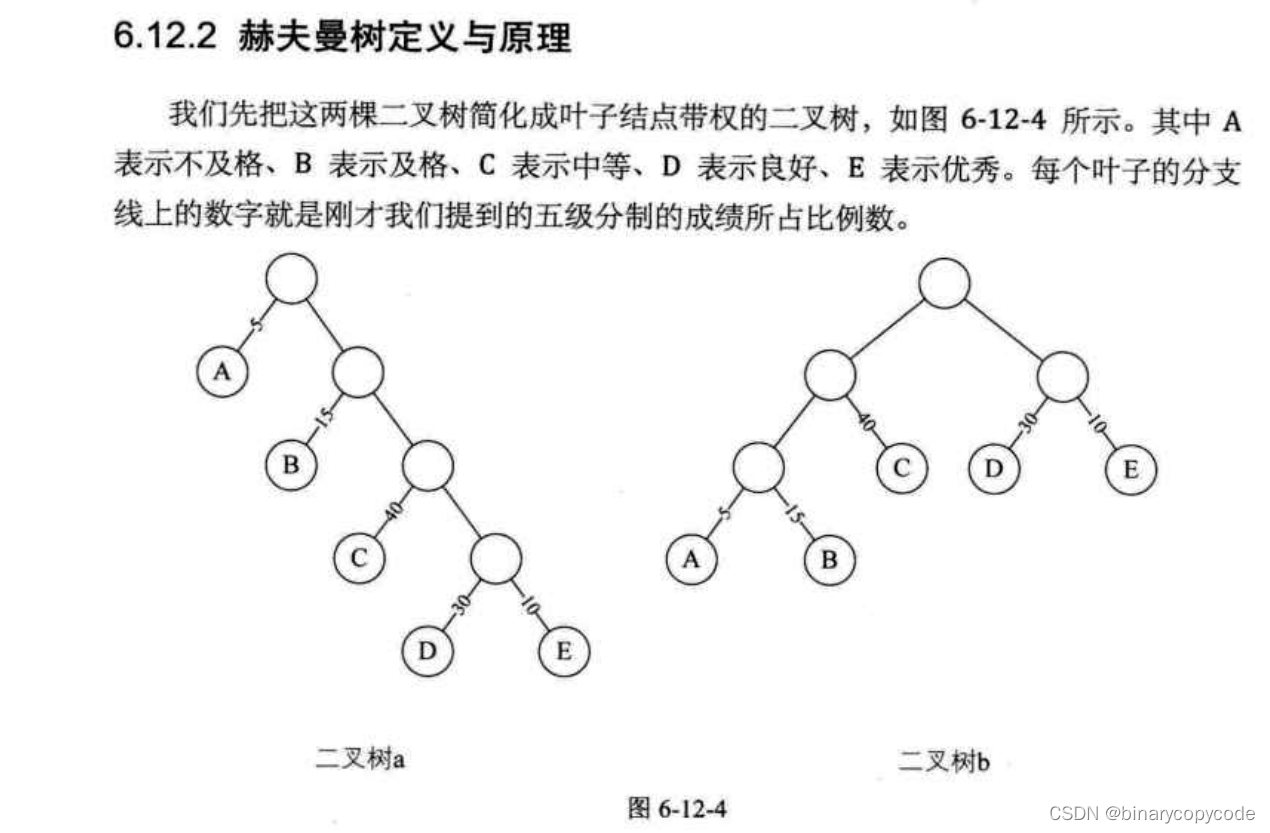
在这里插入图片描述
相当于把一个带权重的树进行重排，排成一个考虑权重最优的二叉树。

构造步骤

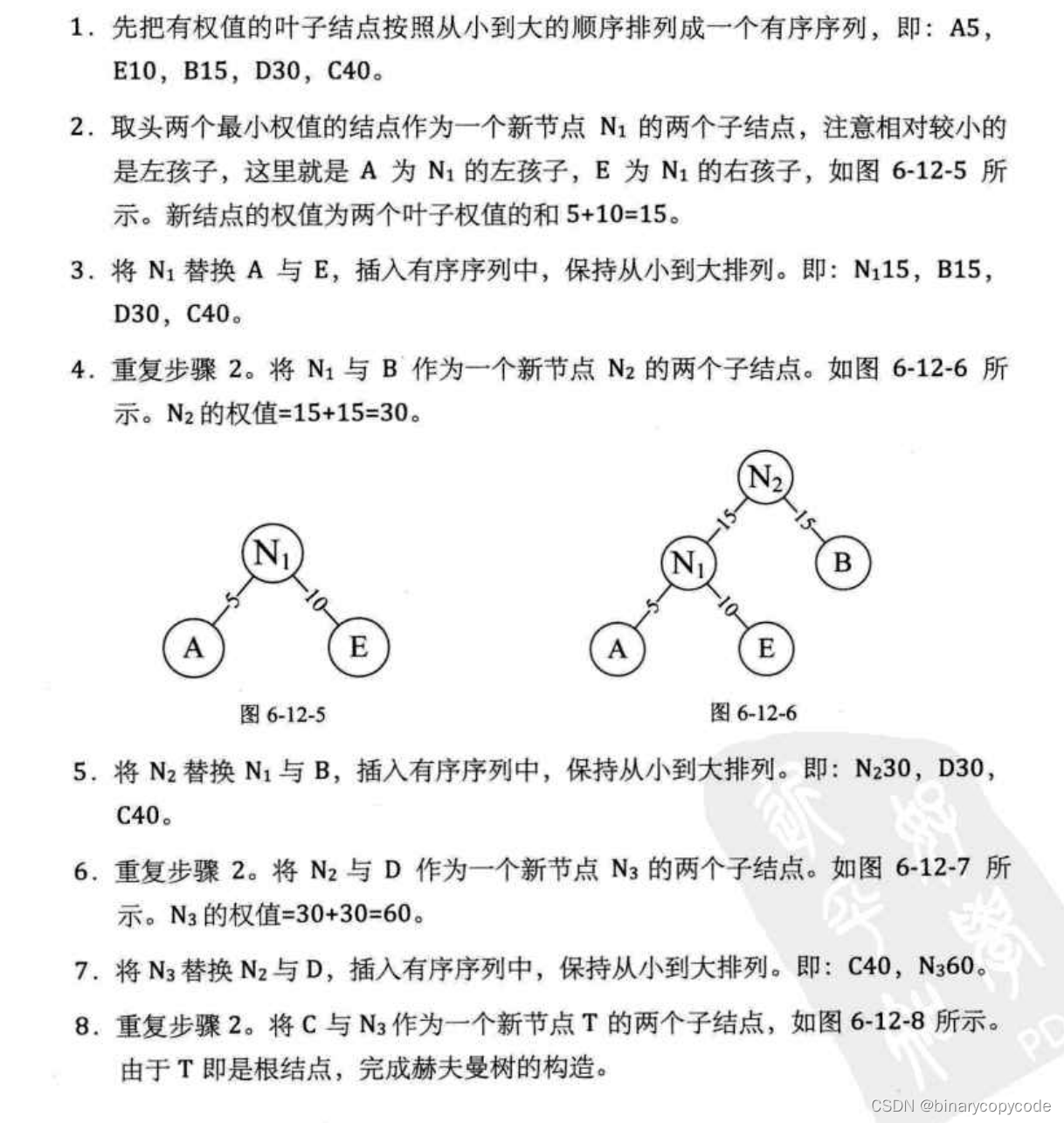
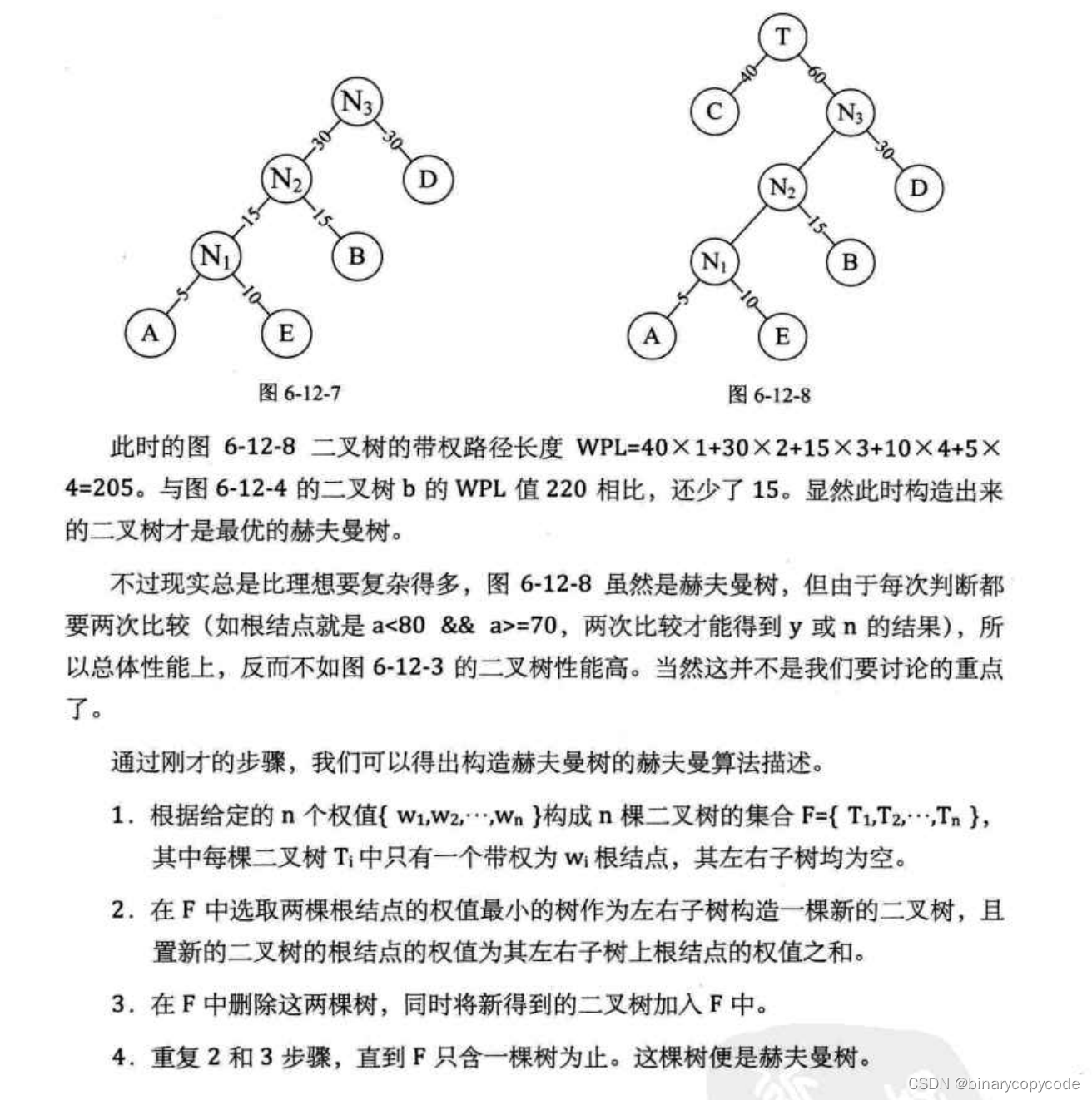
在这里插入图片描述

两个权重相同的直接连接，权重不相同的按照权重小的为左孩子，权重大的为右孩子的原则，进行排列。

遍历

把非线性的树转化成非线性的序列。

先序遍历

先访问根节点，再先序访问左子树，再先序访问右子树。假设二叉树如下：
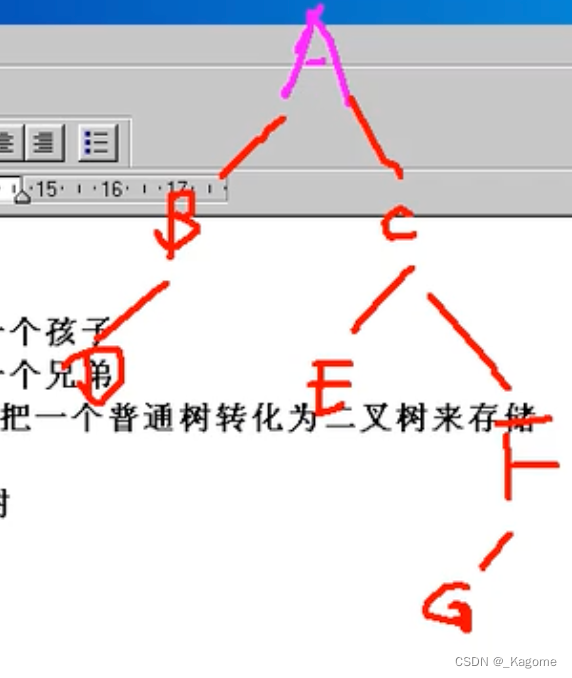
在这里插入图片描述

运用递归的思想，先访问根节点A，再先序访问左子树，再先序访问右子树。在访问左子树的时候，因为左子树也是一棵树，所以会又绕到了先访问根节点B，再顺着来看左子树与右子树，即B的左子树为D，B没有右子树，因为D没有左子树以及右子树，为空，则此次递归结束，BD访问完毕；紧接着先序遍历A的右子树，右子树是个二叉树，再从根节点开始，再遍历左子树，再遍历右子树。都访问完毕之后，才是访问完毕。
eg:
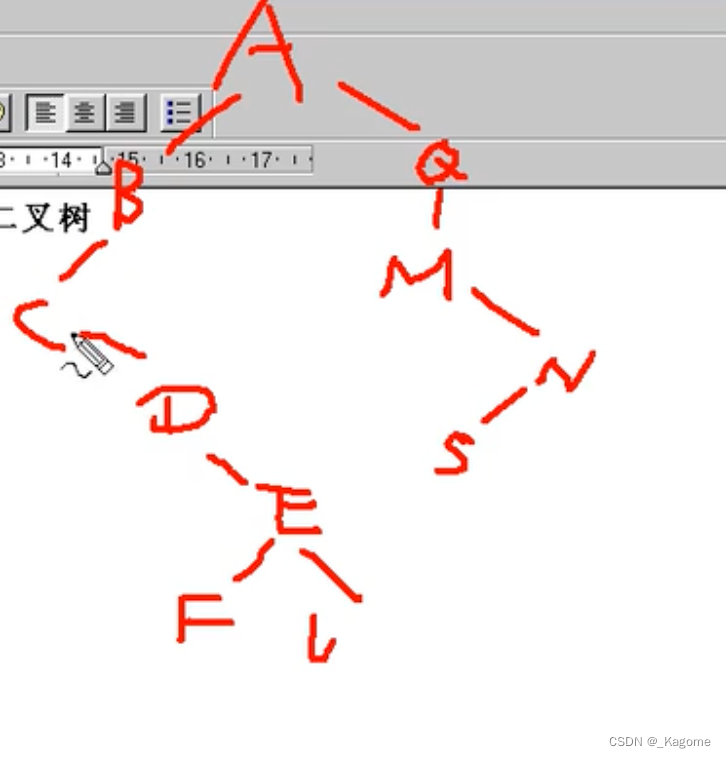
在这里插入图片描述
最后的遍历节点就是ABCDEFLQMNS。

中序遍历

中序遍历左子树，再访问根节点，再中序遍历右子树。
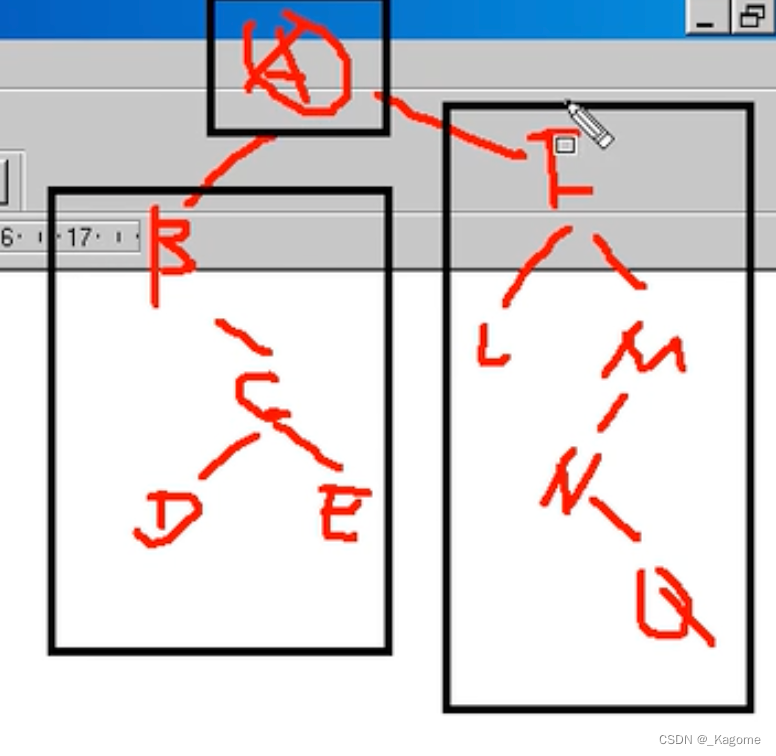
在这里插入图片描述
先中序遍历左子树，B的左子树为空，所以先访问左子树的根节点，即为B，所以先B，B访问完访问B的右子树，也是非空的，所以递归思想，B的右子树先去中序遍历左子树，B的左子树为C的左子树，所以先访问D，再访问根节点C，再访问E。
最后顺序为BDCEALFNQM

eg：
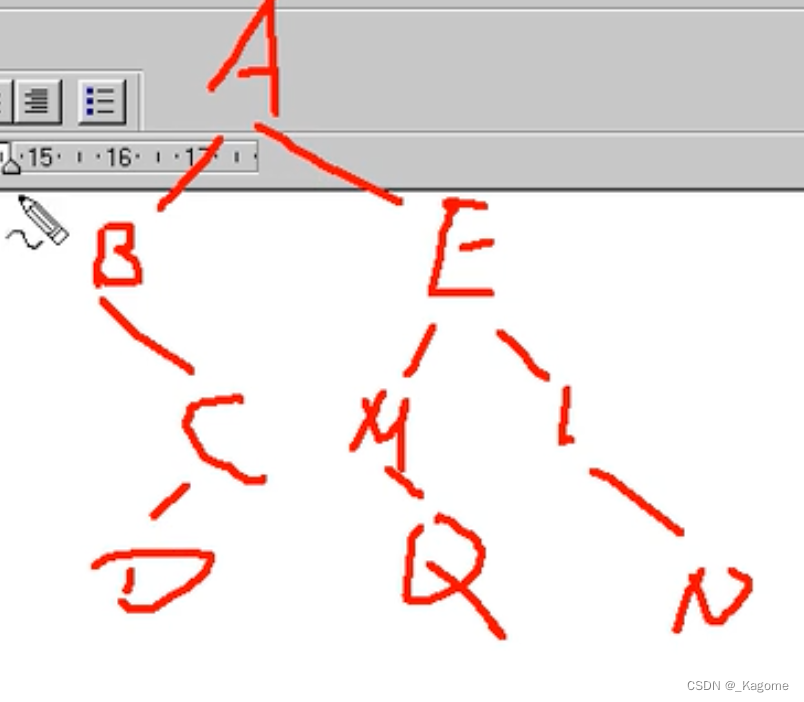
在这里插入图片描述

遍历顺序：BDCAMQELN

后续遍历

中序遍历左子树，中序遍历右子树，再访问根节点。遍历都是以根节点的顺序来判断的。
eg：
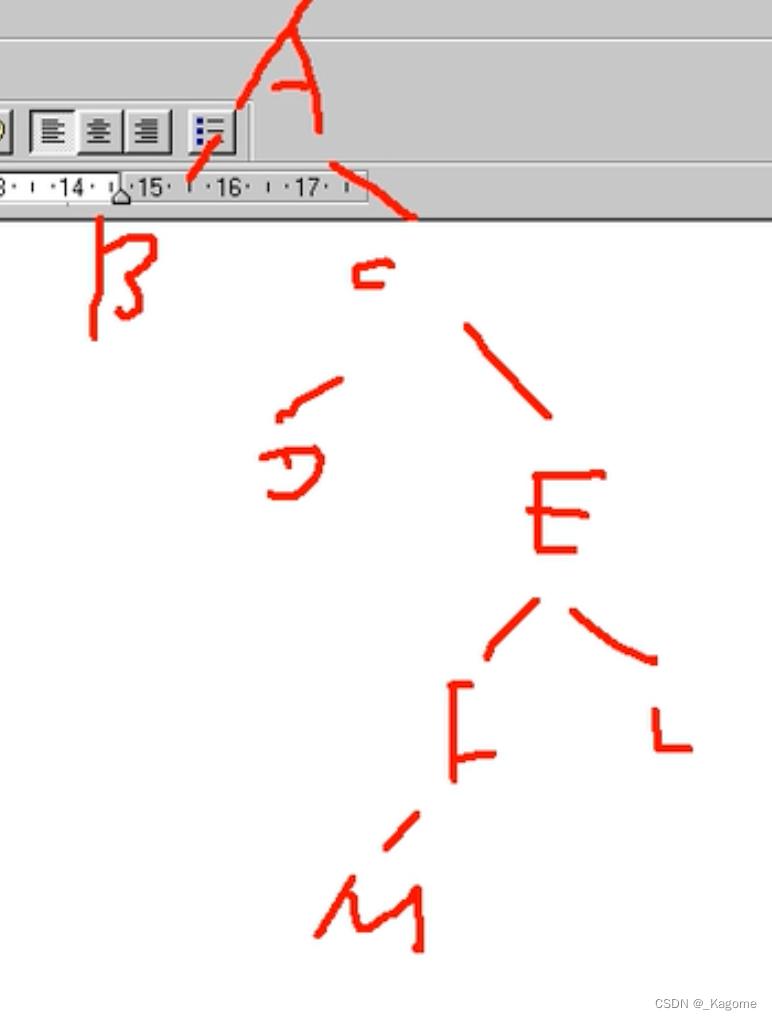
在这里插入图片描述

遍历顺序：BDMFLECA（先全部的左，再全部的右，最后根）

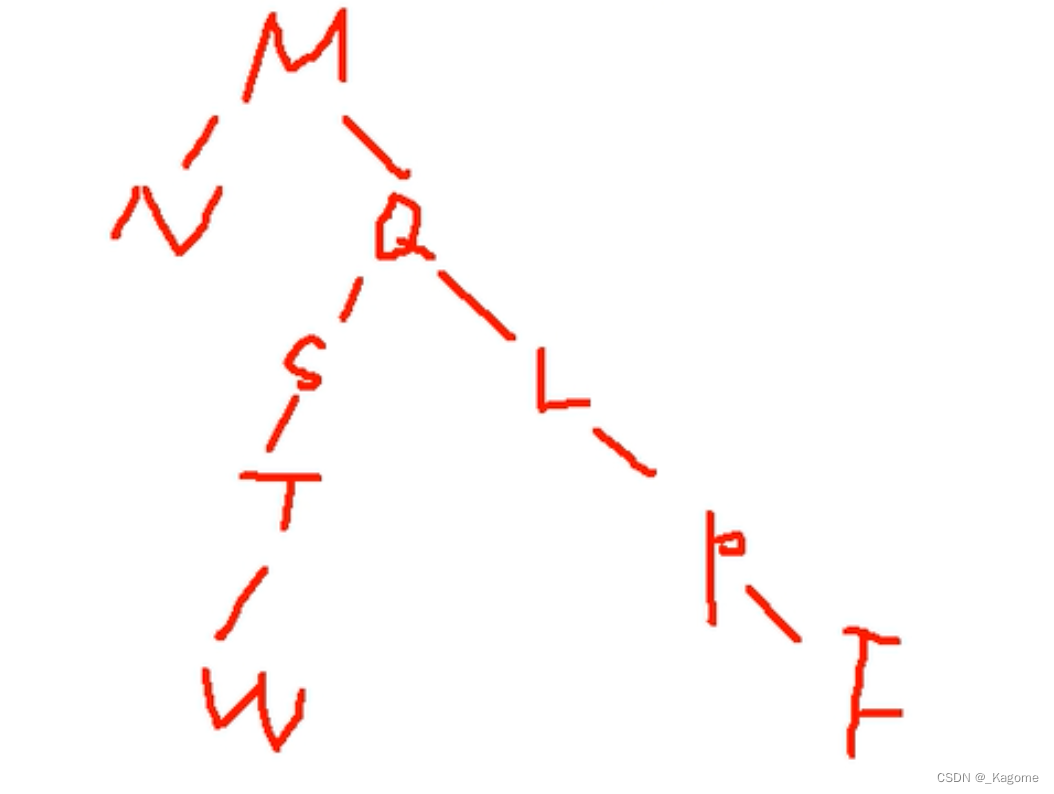
在这里插入图片描述

遍历顺序：NWTSFPLQM

链式二叉树遍历具体代码

# include <stdio.h>
# include <malloc.h>

struct BTNode
{
	char data;
	struct BTNode * pLchild; 
	struct BTNode * pRchild;
};

void PostTraverseBTree(struct BTNode * pT);
struct BTNode * CreateBTree(void);
void PreTraverseBTree(struct BTNode * pT);
void InTraverseBTree(struct BTNode * pT);

int main(void)
{
	struct BTNode * pT = CreateBTree();
	
//	PreTraverseBTree(pT);
//	InTraverseBTree(pT);
	PostTraverseBTree(pT);
	
	return 0;
}

void PostTraverseBTree(struct BTNode * pT)
{
	if (NULL != pT)
	{
		if (NULL != pT->pLchild)
		{
			PostTraverseBTree(pT->pLchild);
		}	
		if (NULL != pT->pRchild)
		{
				PostTraverseBTree(pT->pRchild);
		}
		printf("%c\n", pT->data);
	}
}

void InTraverseBTree(struct BTNode * pT)
{
	if (NULL != pT)
	{
		if (NULL != pT->pLchild)
		{
			InTraverseBTree(pT->pLchild);
		}
		
		printf("%c\n", pT->data);
	
		if (NULL != pT->pRchild)
		{
				InTraverseBTree(pT->pRchild);
		}	
	}
}

void PreTraverseBTree(struct BTNode * pT)
{
	if (NULL != pT)
	{
		printf("%c\n", pT->data);
	
		if (NULL != pT->pLchild)
		{
			PreTraverseBTree(pT->pLchild);
		}
		
		if (NULL != pT->pRchild)
		{
				PreTraverseBTree(pT->pRchild);
		}	
	}	
}

struct BTNode * CreateBTree(void)
{
	struct BTNode * pA = (struct BTNode *)malloc(sizeof(struct BTNode));
	struct BTNode * pB = (struct BTNode *)malloc(sizeof(struct BTNode));
	struct BTNode * pC = (struct BTNode *)malloc(sizeof(struct BTNode));
	struct BTNode * pD = (struct BTNode *)malloc(sizeof(struct BTNode));
	struct BTNode * pE = (struct BTNode *)malloc(sizeof(struct BTNode));

	pA->data = 'A';
	pB->data = 'B';
	pC->data = 'C';
	pD->data = 'D';
	pE->data = 'E';

	pA->pLchild = pB;
	pA->pRchild = pC;
	pB->pLchild = pB->pRchild = NULL;
	pC->pLchild = pD;
	pC->pRchild = NULL;
	pD->pLchild = NULL;
	pD->pRchild = pE;
	pE->pLchild = pE->pRchild = NULL;

	return pA;
}

已知两种遍历序列求原始二叉树

单纯的知道先中后三种序列当中的任何一个，都不能把原始的二叉树序列还原回来，当已知两种序列，可以推出原始的二叉树。

已知先序和中序求后序

示例1：
先序：ABCDEFGH
中序：BDCEAFHG
求后序：因为根据先序，第一个访问的一定是根节点，所以根节点为A，再中序，中间的A确定是根节点，A旁边的是左子树，A右边的是右子树。确定了左子树BDCE与右子树FHG，现在分别找左右子树的根节点，由先序序列可知，先出现的肯定为根。之后确定根节点为BF，之后确定下一个根节点为C，因为中序先遍历左子树，所以D是C的左子树，E就是C的右子树，至此，A的左子树全部推完。右子树类似，推完F，发现在中序序列当中F左边没有点了，说明F没有左子树，只有右子树G，G的左边有H，所以H是G的左子树。
所以后序序列就是DECBHGFA
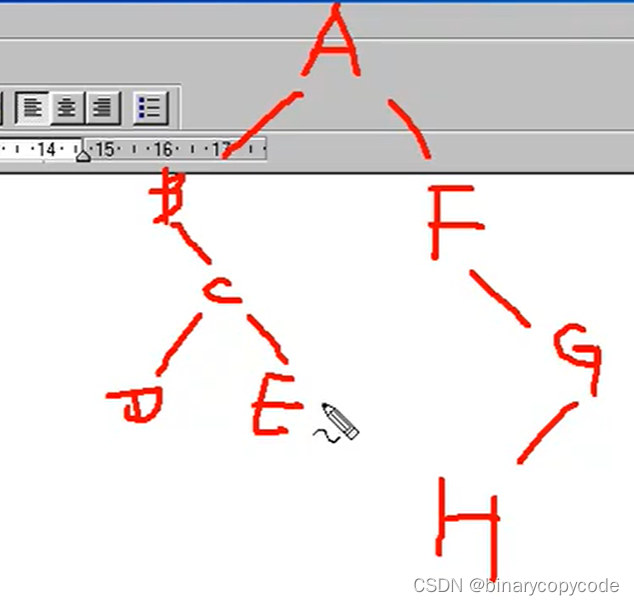
在这里插入图片描述
示例2：
先序：ABDGHCEFI
中序：GDHBAECIF
求后序：根节点为A，A的左子树为GDHB，右子树为ECIF，左子树当中，第一个根节点为B，B的左子树为GDH，D又为根节点，所以GH为其两树，G为左子树，H为右子树，至此A的左子树完全推出；A的右子树为ECIF，在ECIF当中，C为根节点，C的左子树为E，C的右子树为F，F的左子树为I，至此，A的右子树完全推出。
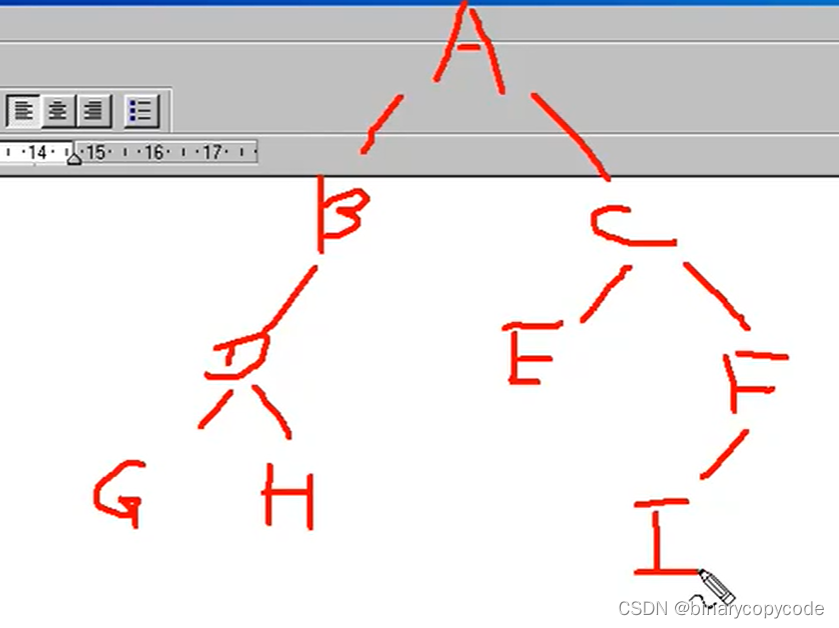
在这里插入图片描述
后序即为：GHDBIEFCA

已知中序和后序求先序

中序：BDCEAFHG
后序：DECBHGFA
求先序：根节点为A，最后出现的后序节点是根节点。所以BDCE是左子树，FHG是右子树。F是根节点，B也是根节点，因为在各个组合中最后出现（依照后序）再在中序中查找，B没有左子树，只有右子树DCE，C在后序最后出现，是根（哪一个在后序最后出现，哪一个就是根），所以C又有左子树又有右子树，左子树为D，右子树为E，至此A的左子树全部推完；A的右子树是FHG，F是根节点，F只有右子树HG，根节点为G，G有左子树H，至此，A的右子树全部推完。
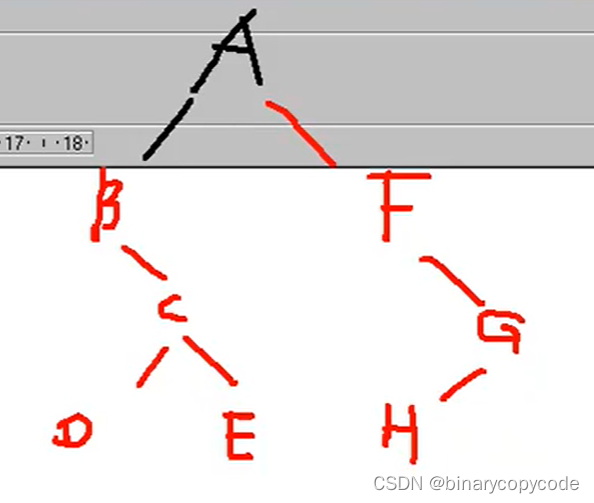
在这里插入图片描述
先序：ABCDEFGH