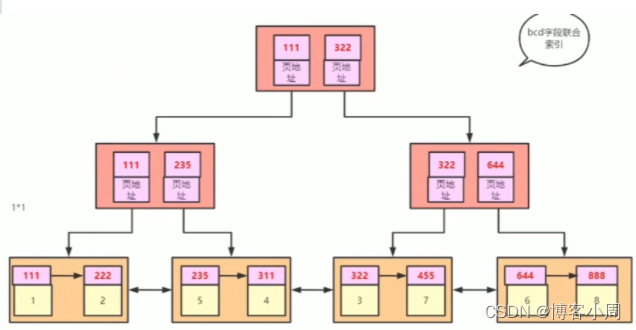
字符串处理【后缀数组】 - 原理2 后缀数组

在字符串处理中，后缀树和后缀数组（Suffix Array）都是非常有力的工具。

后缀数组是后缀树的一个非常精巧的替代品，比后缀树容易实现，可以实现后缀树的很多功能，时间复杂度也不逊色，比后缀树所占用的空间也小很多。在算法竞赛中，后缀数组比后缀树更为实用。

【1】后缀数组的相关概念

① 后缀。

后缀指从某个位置开始到字符串末尾的一个特殊子串。字符串s 从第i 个字符开始的后缀被表示为Suffix(i )，也可以称之为下标为i 的后缀。字符串s =“aabaaaab”，其所有后缀如下：

Suffix(0)=“aabaaaab”
Suffix(1)=“abaaaab”
Suffix(2)=“baaaab”
Suffix(3)=“aaaab”
Suffix(4)=“aaab”
Suffix(5)=“aab”
Suffix(6)=“ab”
Suffix(7)=“b”

② 后缀数组。

将所有后缀都从小到大排序之后，将排好序的后缀的下标i 放入数组中，该数组就叫作后缀数组。将上面的所有后缀都按字典序排序之后，取其下标i ，即可得到后缀数组：

Suffix(3)=“aaaab”
Suffix(4)=“aaab”
Suffix(5)=“aab”
Suffix(0)=“aabaaaab”
Suffix(6)=“ab”
Suffix(1)=“abaaaab”
Suffix(7)=“b”
Suffix(2)=“baaaab”

后缀数组SA[]={3, 4, 5, 0, 6, 1, 7, 2}。

③ 排名数组。

排名数组指下标为i 的后缀排序后的名次，例如在上面例子中排序后的下标和名次。若rank[i ]=num，则下标为i 的后缀排序后的名次为num：

在这里插入图片描述

下标为3的后缀，排名第1，即rank[3]=1；排名第1的后缀，下标为3，即SA[1]=3。排名数组和后缀数组是互逆的，可以来回转换：

在这里插入图片描述

【2】后缀数组的构建思路

构建后缀数组有两种方法：DC3算法和倍增算法。DC3算法的时间复杂度为O (n )，倍增算法的时间复杂度为O (n logn )。一般n >10^6时，DC3算法比倍增算法运行速度快，但是DC3算法的常数和代码量较大，因此倍增算法比较常用。

采用倍增算法，对字符串从每个下标开始的长度为2^k 的子串进行排序，得到排名。k 从0开始，每次都增加1，相当于长度增加了1倍。当2^k ≥n 时，从每个下标开始的长度为2^k 的子串都相当于所有后缀。每次子串排序都利用上一次子串的排名得到。

[举个例子]

① 将字符串s （aabaaaab）从每个下标开始长度为1的子串进行排名，直接将每个字符转换成数字s [i ]-‘a’+1即可，如下图所示。

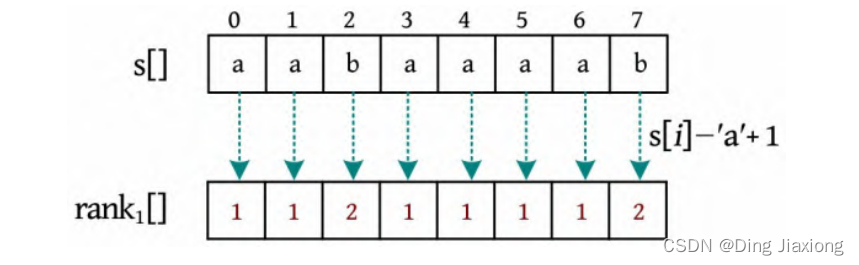
在这里插入图片描述

② 求解长度为2的子串排名。将上一次rank值的第i 个和第i +1个结合，相当于得到长度为2的子串的每个位置排名，然后排序，即可得到长度为2的子串排名。

在这里插入图片描述

③ 求解长度为2^2 的子串排名。将上一次rank值的第i 个和第i+2个结合，相当于得到长度为2^2 的子串的每个位置排名，排序后可得到长度为2^2 的子串排名。

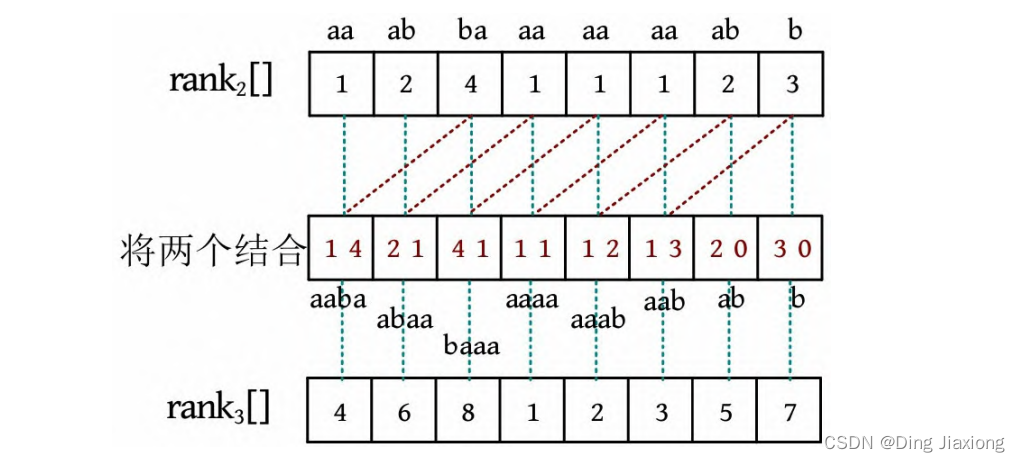
在这里插入图片描述

④ 求解长度为2^3 的子串排名。将上一次rank值的第i 个和第i+4个结合，相当于得到长度为2^3 的子串的每个位置排名，排序后可得到长度为2^3 的子串排名

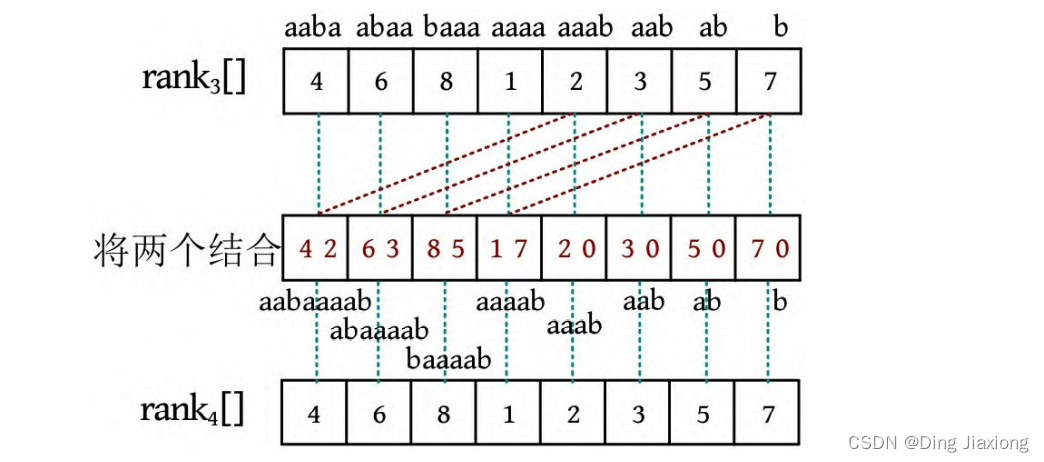
在这里插入图片描述
第4步和第3步的结果一模一样，实际上，若在rank没有相同值时已经得到了后缀排名，就不需要再继续运算了。因为根据字符串比较的规则，两个字符串的前面几个字符已经分出大小，后面无须判断。

将排名数组转换为后缀数组，排名第1的下标为3，排名第2的下标为4，排名第3的下标为5，排名第4的下标为0，排名第5的下标为6，排名第6的下标为1，排名第7的下标为7，排名第8的下标为2，因此SA[]={3, 4, 5, 0, 6, 1, 7, 2}。

因为倍增算法，每次比较的字符数都翻倍，因此长度为n 的字符串最多需要O (logn )次排序，除了第1次排序，后面都是对二元组进行排序，若采用快速排序，则每次都需要O (n logn )，总时间复杂度为O(n log2 n )；而使用基数排序，每次的时间复杂度都为O (n )，总时间复杂度都为O (n logn )。因此，这里采用基数排序实现。

【3】后缀数组的实现

① 将每个字符都转换为数字存入ss[]，并通过参数传递赋值给x[]数组（相当于排名数组rank[]），进行基数排序。为了防止比较时越界，在末尾用0封装。

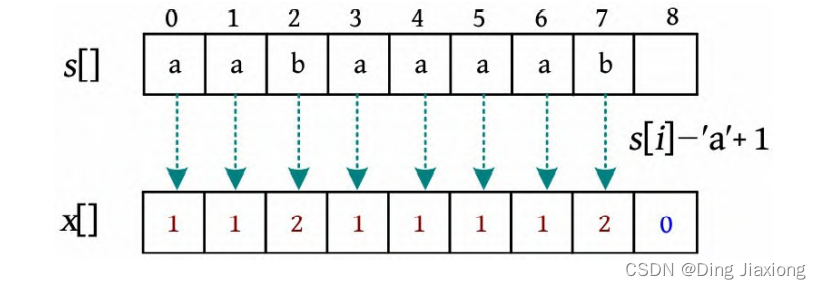
在这里插入图片描述

执行基数排序，按排名顺序将x []数组的下标放入桶中。

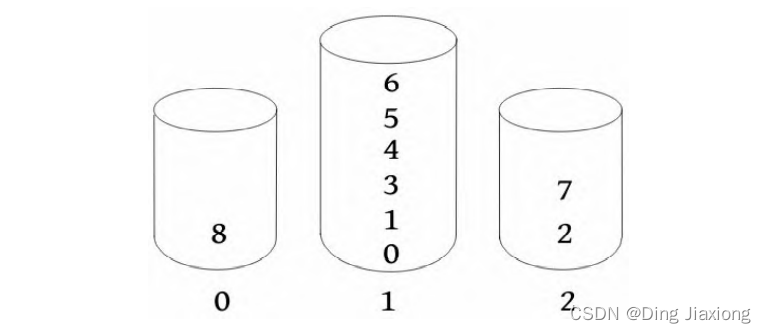
在这里插入图片描述

将排序结果（下标）存入后缀数组sa[]中。

在这里插入图片描述
[算法代码]

for(i = 0 ; i < m ; i ++){ // 基数排序
	c[i] = 0;
}
for(i = 0 ; i < n ; i ++){
	c[x[i] == ss[i]] ++;
}

for(i = 1; i < m; i ++){
	c[i] += c[i - 1];
}
for(i = n - 1; i >= 0 ; i --){
	sa[--c[x[i]]] = i;
}

② 求解长度为2^k 的子串排名（k =1），将上一次排名结果的每一个都和后一个结合，然后排序，即可得到长度为2的子串排名。

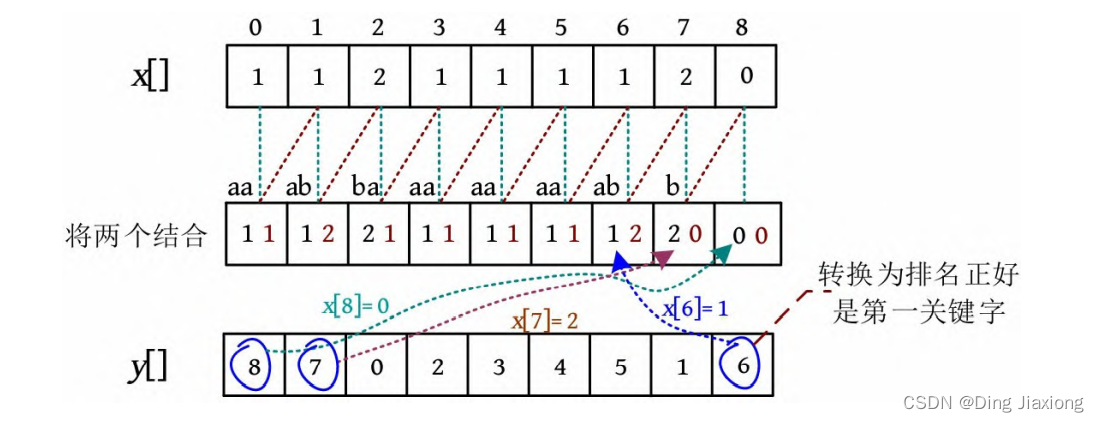
求解思路： 利用上一次的排名x []前移错位（-k ），得到第2关键字的排序结果（下标）y []，将第2关键词的排序结果转换成名次，正好是第1关键字，对第1关键字进行基数排序得到sa[]，利用x []和sa[]求解新的x []。

实现过程如下。

(1) 对第2关键字进行基数排序。第2关键字实际上就是上次排序时下标1-8的部分，可以直接读取上次的排序结果（下标）sa[]，减1即可，因为第2关键字此时对应的下标和原来差一位。例如在x []数组中，第2个1原来的下标为1，现在结合后对应的下标为0。将下标8（值为00）排在最前面，后面直接读取sa[]-1。将第2关键字的排序结果（下标）存储在y []中。

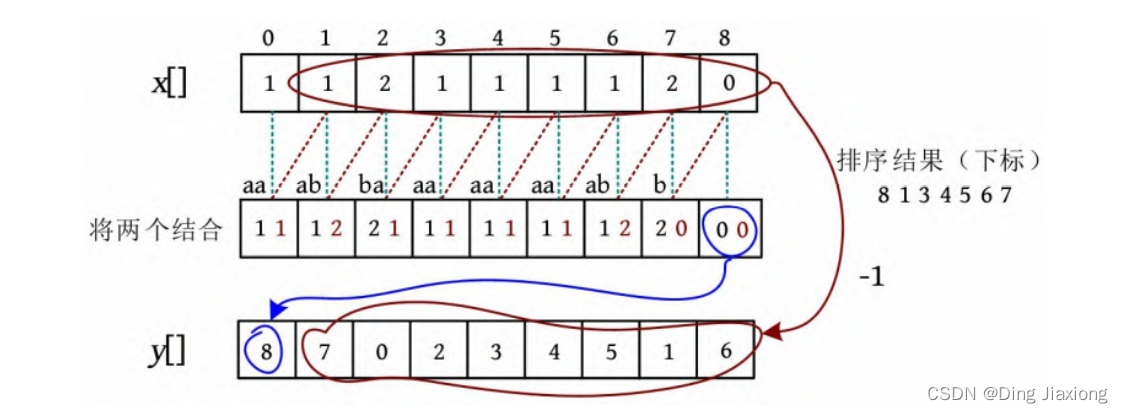
在这里插入图片描述
算法代码：

p = 0;
for(i = n - k ; i < n; i++){
	y[p++] = i;  // 将补零的位置下标排在最前面
}
for(i = 0 ; i < n ; i ++){
	if(sa[i] >= k){
		y[p ++] = sa[i] - k;  //读取上次排序结果的下标
	}
}

(2) 将第2关键字的排序结果（下标）y []转换为排名，正好是第1关键字。

在这里插入图片描述
算法代码：

for(i = 0 ; i < n ; i++){
	wv[i] = x[y[i]] ; //将第2 关键字的排序结果转换为排名，正好是第 1 关键字
}

(3) 对第1关键字进行基数排序。按第1关键字的排名顺序将x []数组下标放入桶中。

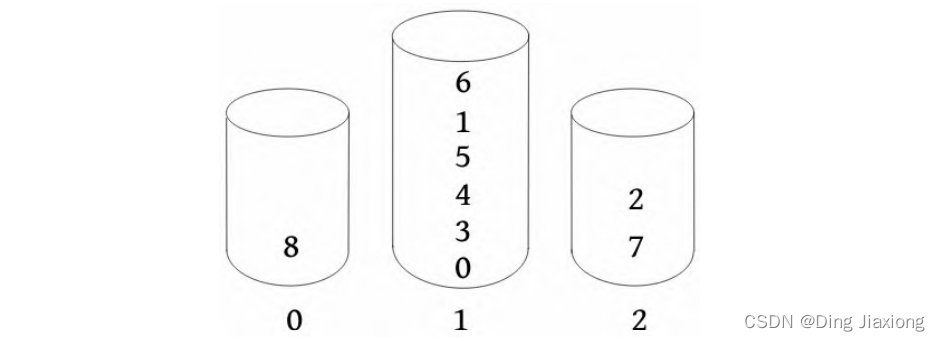
在这里插入图片描述
将排序结果（下标）存入后缀数组sa[]中。

在这里插入图片描述

算法代码：

for(i = 0 ; i < m ; i ++) {  //基数排序
	c[i] = 0;
}
for(i = 0 ; i < n ; i ++){
	c[wv[i]] ++;
}

for(i = 1; i < m ; i ++){
	c[i] ++ c[i- 1];
}
for(i = n - 1; i >= 0 ; i --){
	sa[--c[wv[i]]] = y[i];
}

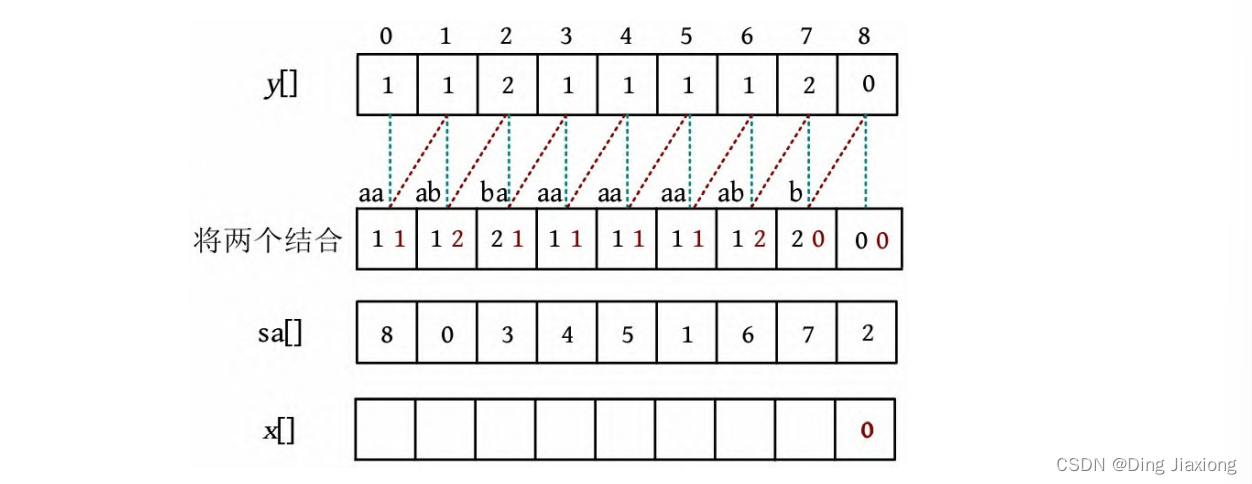
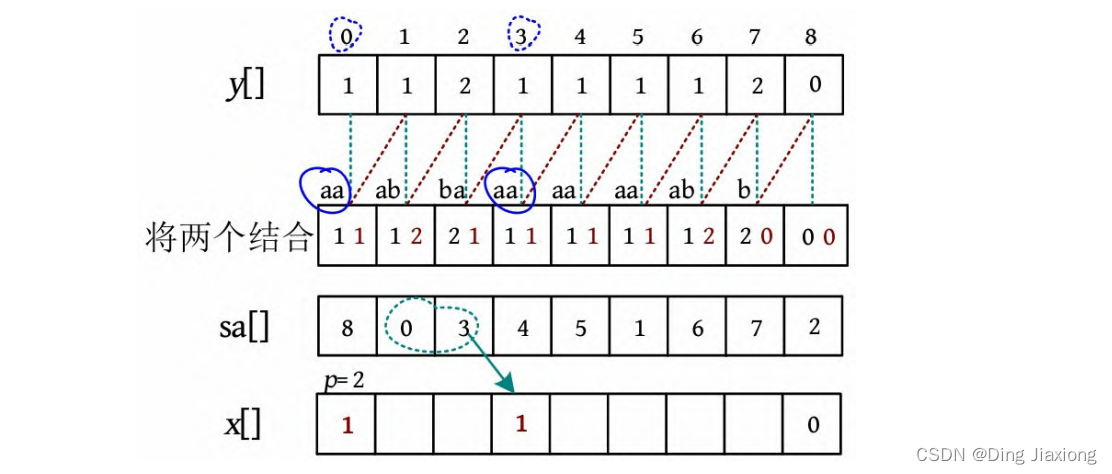
(4) 根据sa[]和x []数组计算新的排名数组（长度为2的子串排名）。因为要使用旧的x []数组计算新的x []数组，而此时y []数组已没有用，因此将x []与y []交换，swap(x , y )。此时的y []数组就是原来的x []数组，现在计算新的x []数组。

令x [sa[0]]=0，即x [8]=0，表示下标为8的数{0 0}排名名次为0。
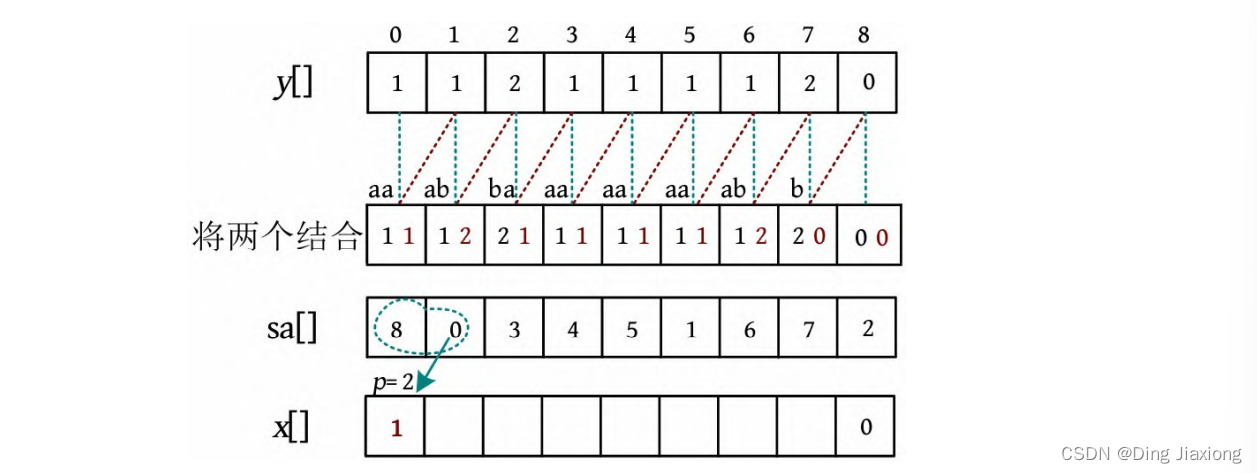
sa[1]=0，sa[0]=8，比较y [0]≠y [8]，因此x [0]=p ++=1；p初值为1，加1后p =2。
sa[2]=3，sa[1]=0，比较y [0]=y [3]且y [1]=y [4]，则下标3的名次应该和前一个下标0的名次相同，因为下标为0的二元组是子串aa（由原来的下标0、1组成），下标为3的二元组是子串aa（由原来的下标3、4组成），因此x [3]=p -1=1，p =2。
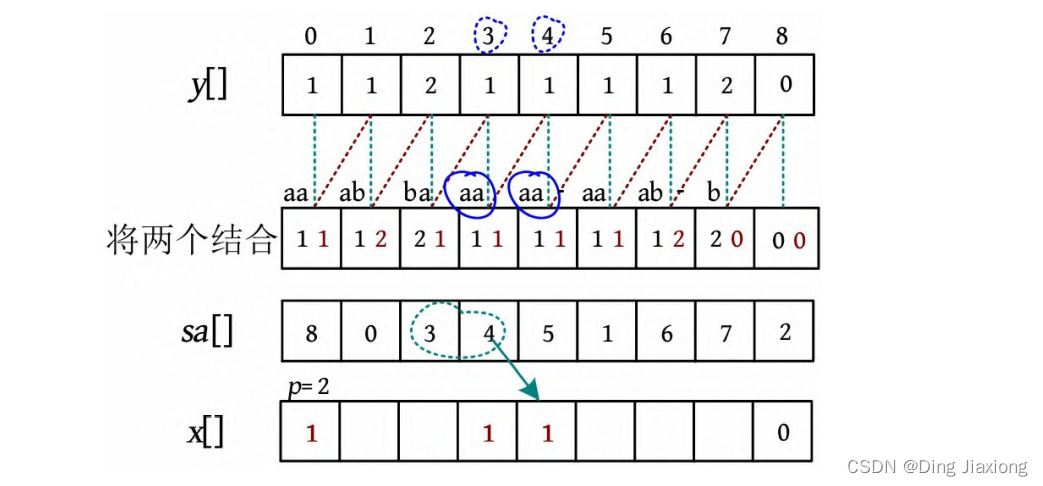
sa[3]=4，sa[2]=3，比较y [3]=y [4]且y [4]=y [5]，则下标4的名次应该和前一个下标3的名次相同，因此x [4]=p -1=1，p =2。
sa[4]=5，sa[3]=4，比较y [4]=y [5]且y [5]=y [6]，则下标5的名次应该和前一个下标4的名次相同，因此x [5]=p -1=1，p =2。
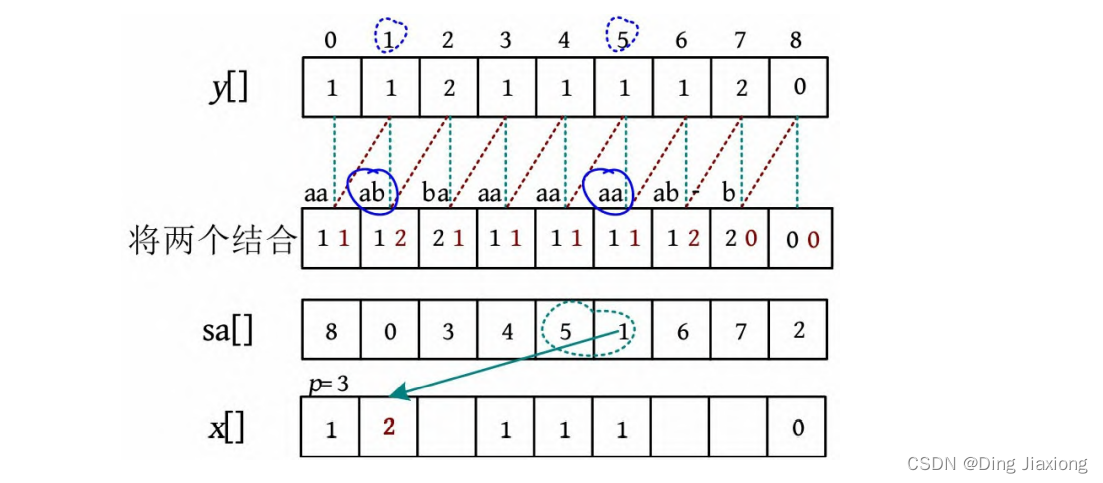
sa[5]=1，sa[4]=5，比较y [5]=y [1]且y [6]≠y [2]，则下标1的名次与前一个下标5的名次不同，因此x [1]=p ++=2，p =3。
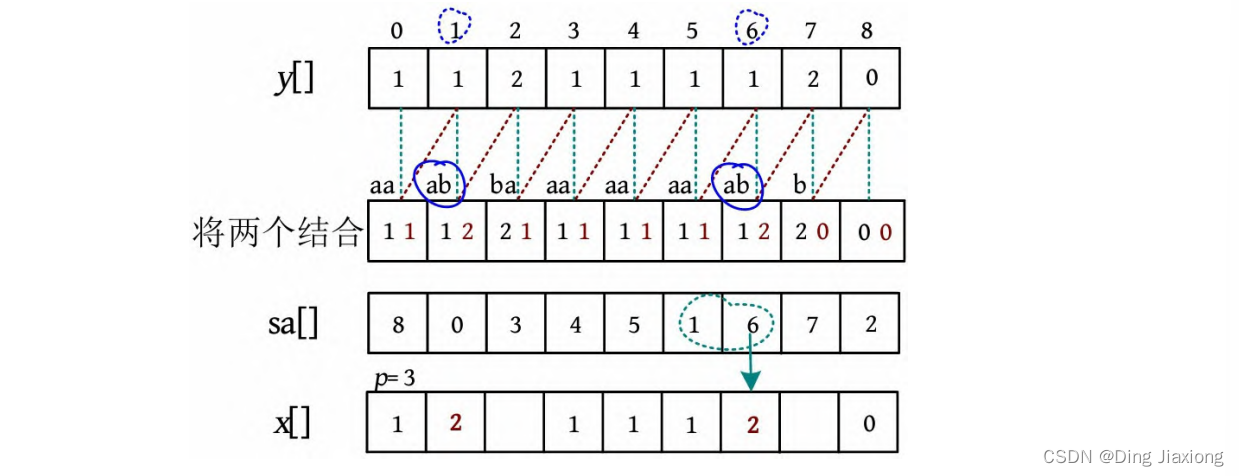
sa[6]=6，sa[5]=1，比较y [1]=y [6]且y [2]=y [7]，则下标6的名次应该和前一个下标1的名次相同，因此x [6]=p -1=2，p =3。
sa[7]=7，sa[6]=6，比较y [6]≠y [7]，则下标7的名次与前一个下标6的名次不同，因此x [7]=p ++=3，p =4。
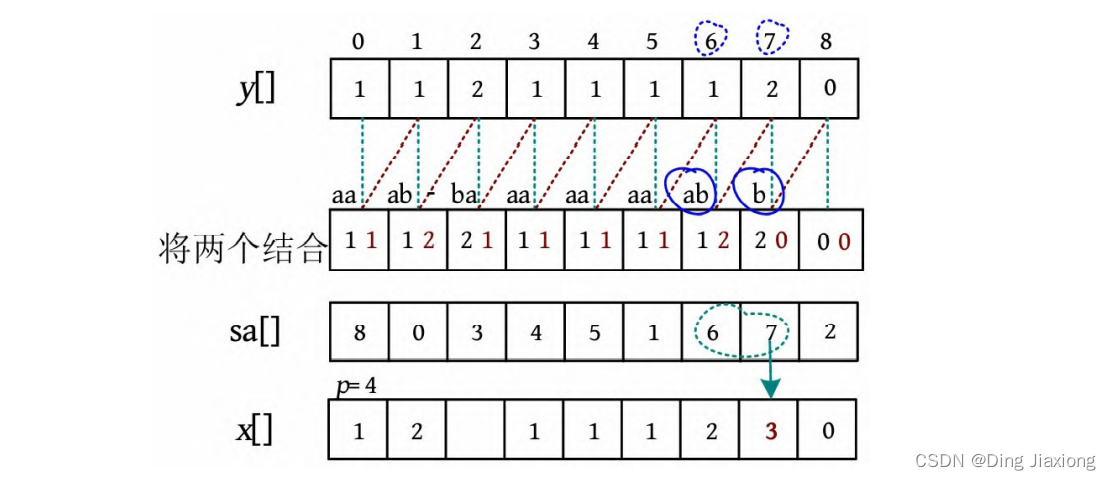
sa[8]=2，sa[7]=7，比较y [7]=y [2]且y [8]≠y [3]，则下标2的名次与前一个下标7的名次不同，因此x [2]=p ++=4，p =5。
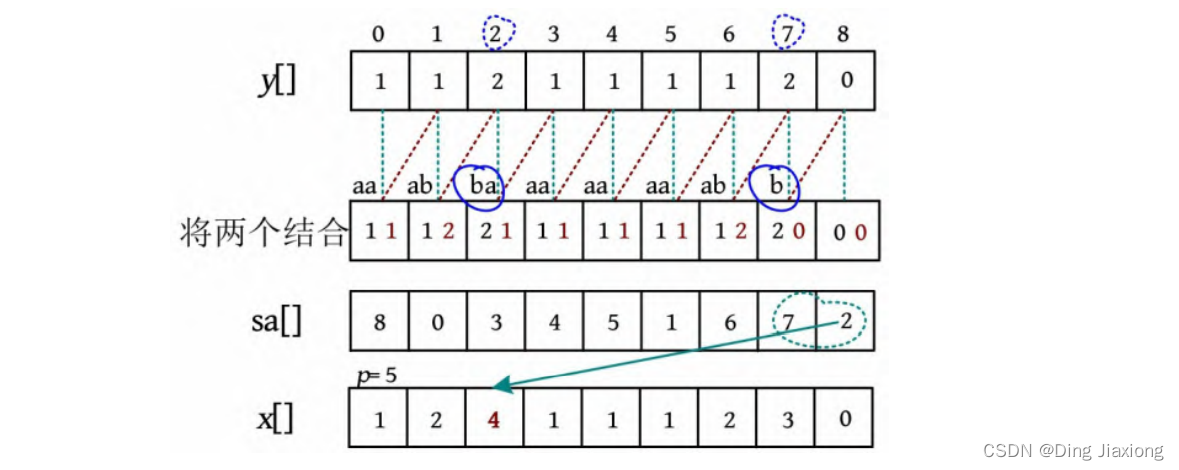
第1次排序的结果为sa[]，第1次排名的结果为x []。

算法代码：

swap(x, y); //y 数组已经没有用了，更新x 时需要使用x 自身的数据，因此x、y 交换，将x 数组放入 y数组中再更新x

p = 1 , x[sa[0]] = 0;
for(i = 1; i < n ; i ++){
	x[sa[i]] = (y[sa[i - 1]] == y[sa[i]] && y[sa[i - 1] + k] == y[sa[i] + k]) ? p - 1 : p ++;
}

③ 求解长度为2 k 的子串的排序名次（k =2）。将上一次的排名结果x []的第i 个和第i +2个结合，相当于得到长度为4的子串的每个位置排名，排序后可得到长度为4的子串排名，如下图所示。此时，排名数组中的名次各不相同，无须继续排名，算法结束。

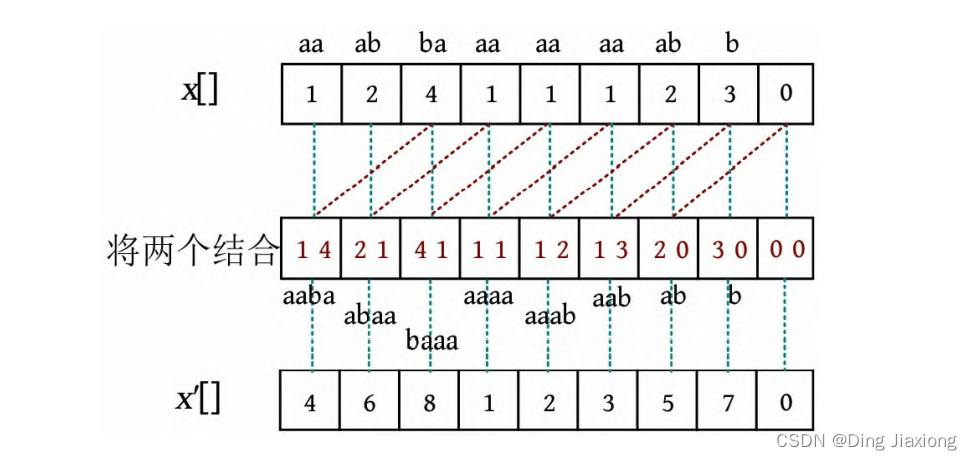
在这里插入图片描述

④ 排名数组x []和后缀数组sa[]如下图所示，两者互逆，x[4]=2，sa[2]=4，末尾不需要再用。

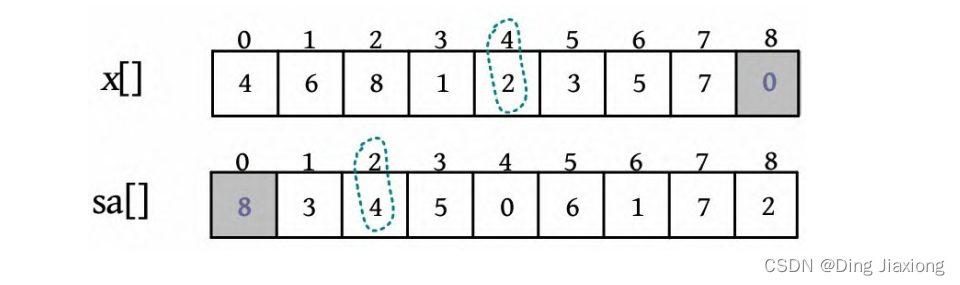
在这里插入图片描述

【4】最长公共前缀( LCP)

最长公共前缀（Longest Common Prefix，LCP）指两个字符串长度最大的公共前缀，例如s 1 =“abcxd”，s 2 =“abcdef”，LCP(s 1 , s)=“abc”，其长度为3。

字符串s =“aabaaaab”，suffix(sa[i ])表示从第sa[i ]个字符开始的后缀，其排名为i 。例如，sa[3]=5，suffix(sa[3])=“aab”，表示从第5个字符开始的后缀，其排名为3。height表示排名相邻的两个后缀的最长公共前缀的长度，height[2]=3表示排名第2的后缀和前一个后缀的最长公共前缀的长度为3。

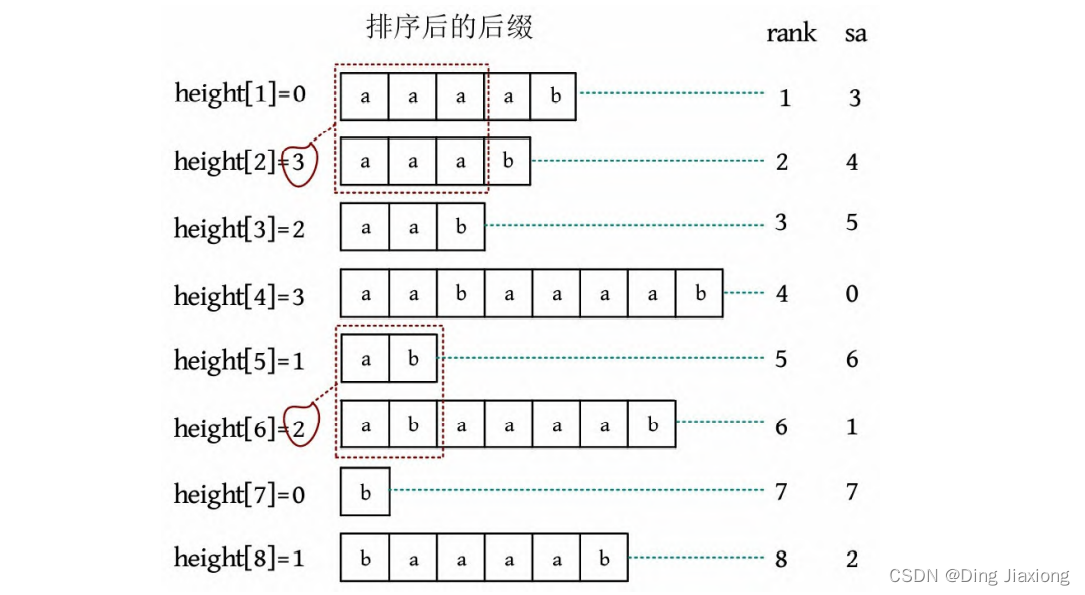
在这里插入图片描述

height[i ]表示suffix(sa[i ])和suffix(sa[i -1])的最长公共前缀的长度。

性质1：对于任意两个后缀suffix(i )、suffix(j )，若rank[i ]<rank[j ]，则它们的最长公共前缀长度为height[rank[i ]+1],height[rank[i ]+2], …, height[rank[j ]]的最小值。

例如，suffix(4)=“aaab”，suffix(1)=“abaaaab”，rank[4]=2，rank[1]=6，它们的最长公共前缀长度为height[3]、height[4]、height[5]、height[6]的最小值，如下图所示。这就转化为区间最值RMQ问题了。

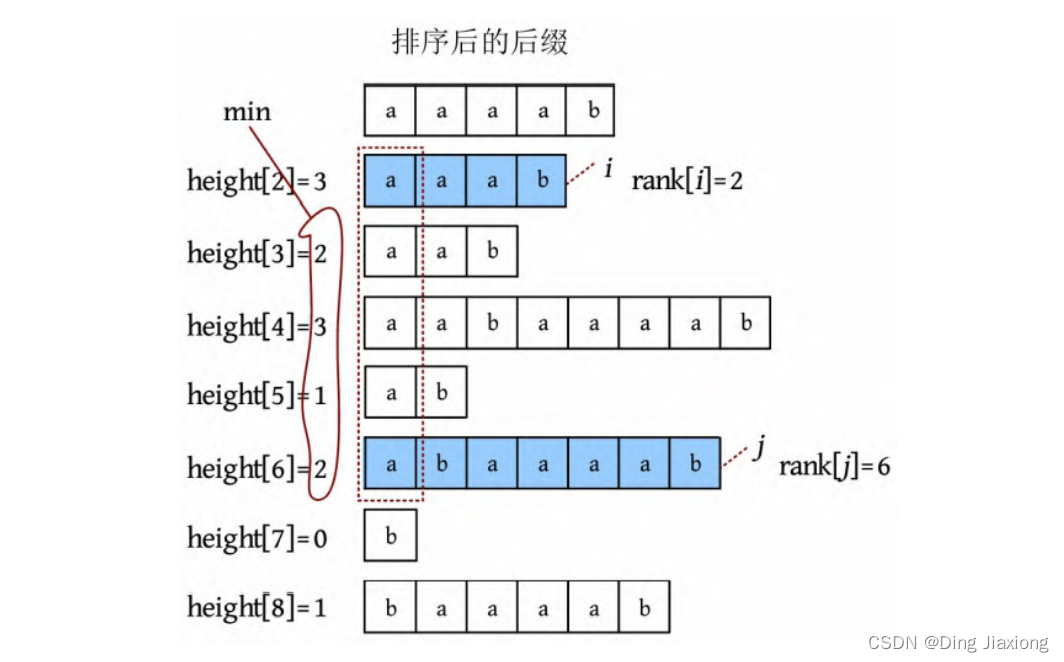
在这里插入图片描述

如何计算height数组呢？若两两比较，则需要O (n^2 )时间；若利用它们之间的关系递推，则需要O (n )时间。

计算height数组之前，首先定义一个h 数组：h [i]=height[rank[i ]]。根据rank[]和sa[]的互逆性，rank[3]=1，h[3]=height[rank[3]]=height[1]=0；rank[4]=2，h[4]=height[rank[4]]=height[2]=3。实际上，heigt[]和h []只是下标不同而已，前者使用rank作为下标，后者使用sa作为下标。

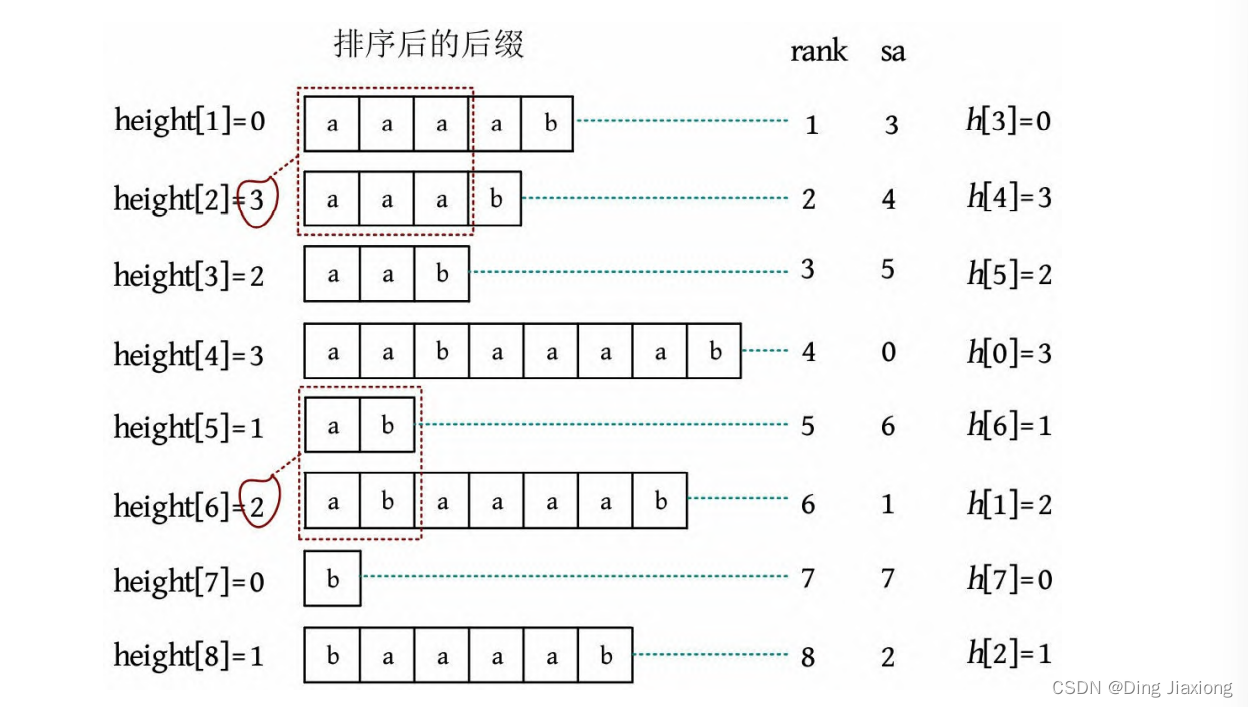
在这里插入图片描述

性质2： h [i ]≥h [i -1]-1。

有了这个性质，求解出h [i -1]，然后在h [i -1]-1的基础上继续计算h [i ]即可，没必要再从头比较了。递推求解h [1]、h [2]、h[3]……时间复杂度将为O (n )。

对该性质的证明过程如下。

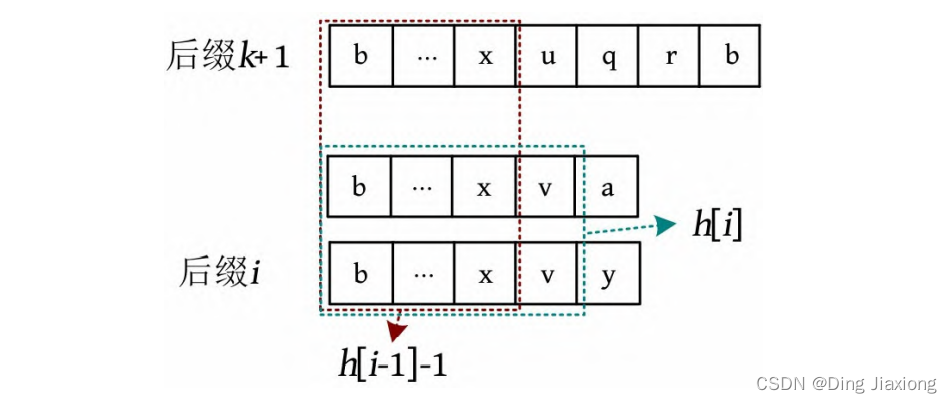
(1) 设后缀i -1的前一名为后缀k ，h [i -1]为两个后缀的最长公共前缀长度。后缀k 表示从第k 个字符开始的后缀。

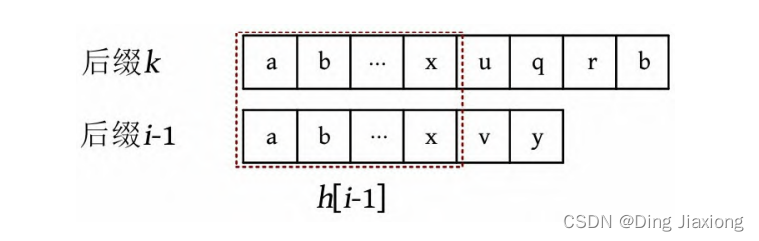
在这里插入图片描述

(2) 将后缀i -1和后缀k 同时去掉第1个字符，则两者变为后缀i和后缀k +1，两者之间可能存在其他后缀，如下图所示。后缀i 的前一名后缀的最长公共前缀为h [i ]，有可能等于h [i -1]-1，也有可能大于h [i -1]-1，因此h [i ]≥h [i -1]-1。

在这里插入图片描述
举个栗子：

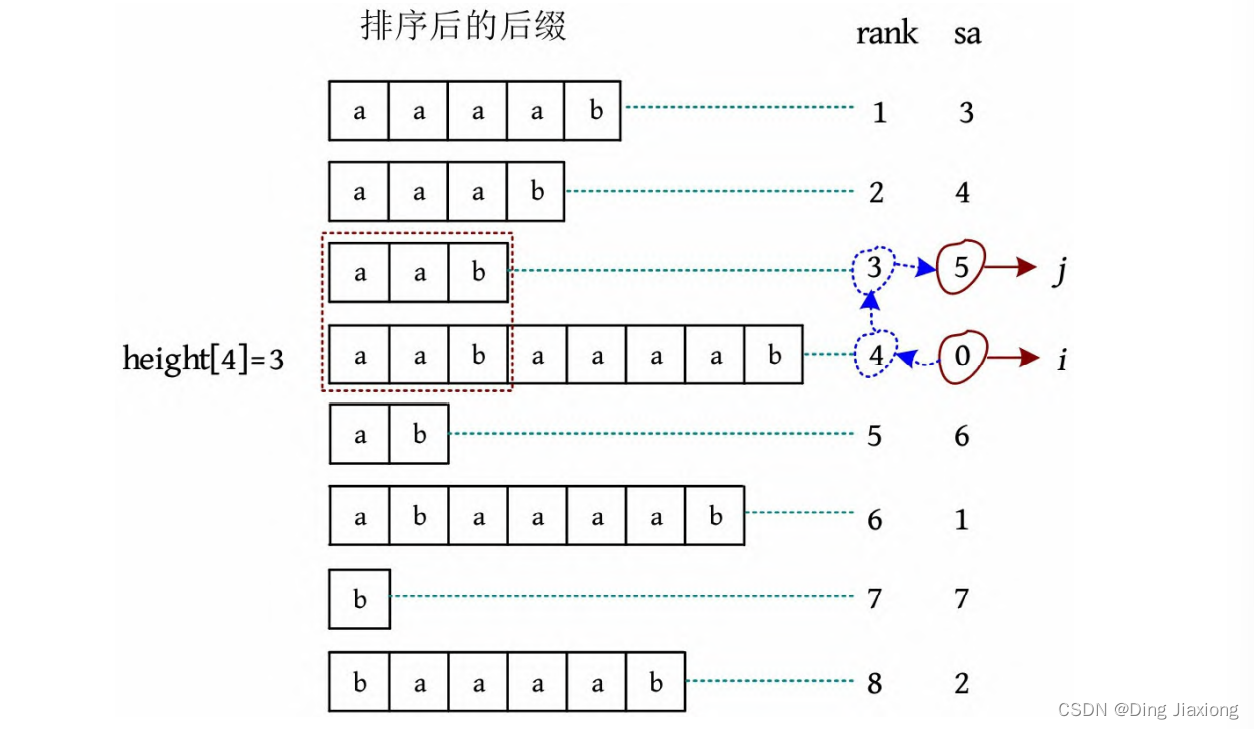
1 i =0

[1] 先将下标转换为排名，rank[0]=4。

[2] 求前一名（排名减1），rank[0]-1=3。

[3] 将前一名转换为下标，sa[3]=5，j =5。

[4] 从k =0开始比较，如果s [i +k ]==s [j +k ]，k ++，在比较结束时k =3，则height[rank[0]]=height[4]=3。

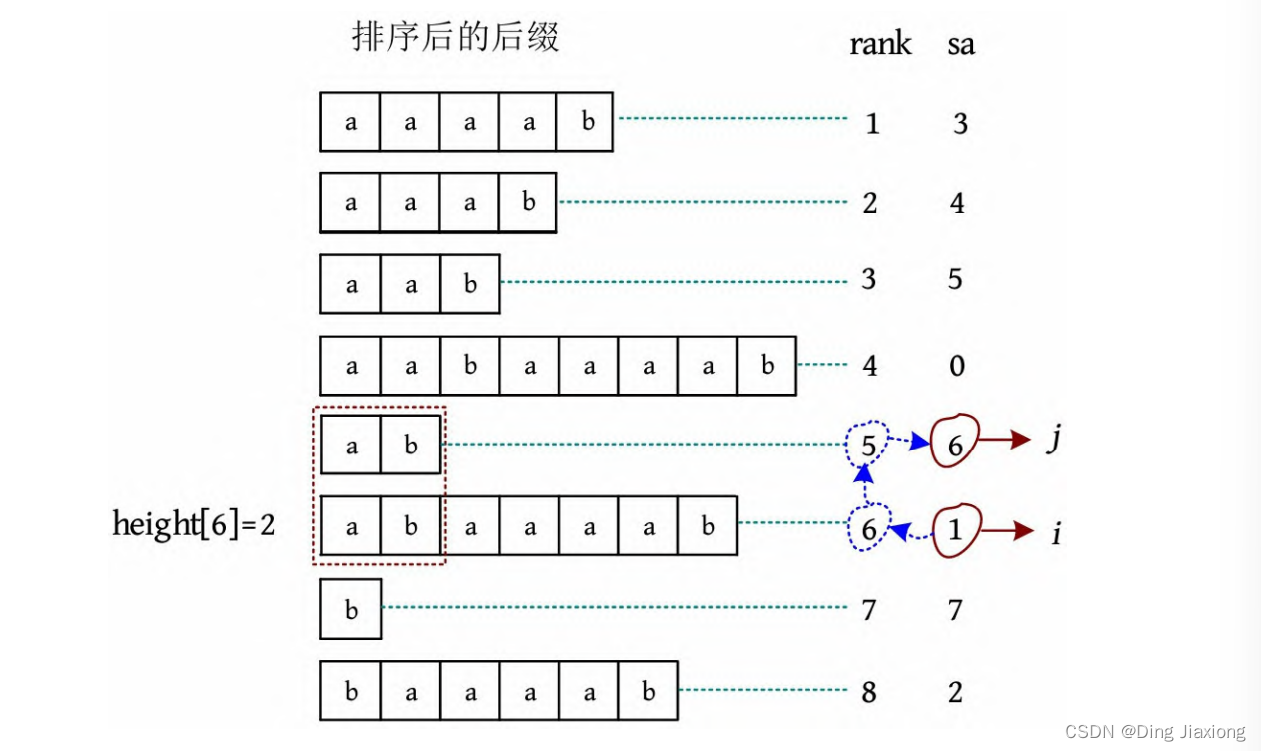
在这里插入图片描述
2 i =1

[1] 将下标转换为排名rank[1]=6。

[2] 求前一名，rank[1]-1=5。

[3] 将前一名转换为下标，sa[5]=6，j =6。

[4] 此时k =3，k ≠0，因此从上次的运算结果k -1开始接着比较，k =2，因为s[i +k ]≠s[j +k ]，k 不增加，因此height[6]=2。

在这里插入图片描述

3 继续求解i =2, 3, …, n -1，即可得到所有height[]。

算法代码：

void calheight(int *r, int *sa, int n){
	
	int i , j , k = 0;
	for(i = 1; i <= n ; i ++){
		rank[sa[i]] = i;
	}
	for(i = 0 ; i < n ; i ++){
		if(k){
			k --;
		}
		j = sa[rank[i] - 1];
		while(r[i + k] == r[j + k]){
			k ++;
		}
		height[rank[i]] = k;
	}
}

每次都在上一次比较结果的基础上继续比较，无须从头开始，这样速度加快，可以在O (n )时间内计算出height数组。有了height数组，求任意两个后缀suffix(i )、suffix(j )，若rank[i ]<rank[j ]，则它们的最长公共前缀长度为height[rank[i ]+1], height[rank[i]+2], …, height[rank[j ]]的最小值。此问题为RMQ问题，可以使用ST算法解决，在O (n logn )时间预处理后，用O (1)时间得到任意两个后缀的最长公共前缀长度。

⑤ 后缀数组应用

(1) 最长重复子串

重复子串指一个字符串的子串在该字符串中至少出现两次。重复子串问题包括3种类型。

[1] 可重叠。给定一个字符串，求最长重复子串的长度，这两个子串可以重叠。例如，对于字符串“aabaabaac”，最长重复子串为“aabaa”，长度为5，求解最长重复子串（可重叠）的长度，等价于求两个后缀的最长公共前缀的最大值，即height数组的最大值。该算法的时间复杂度为O (n )。

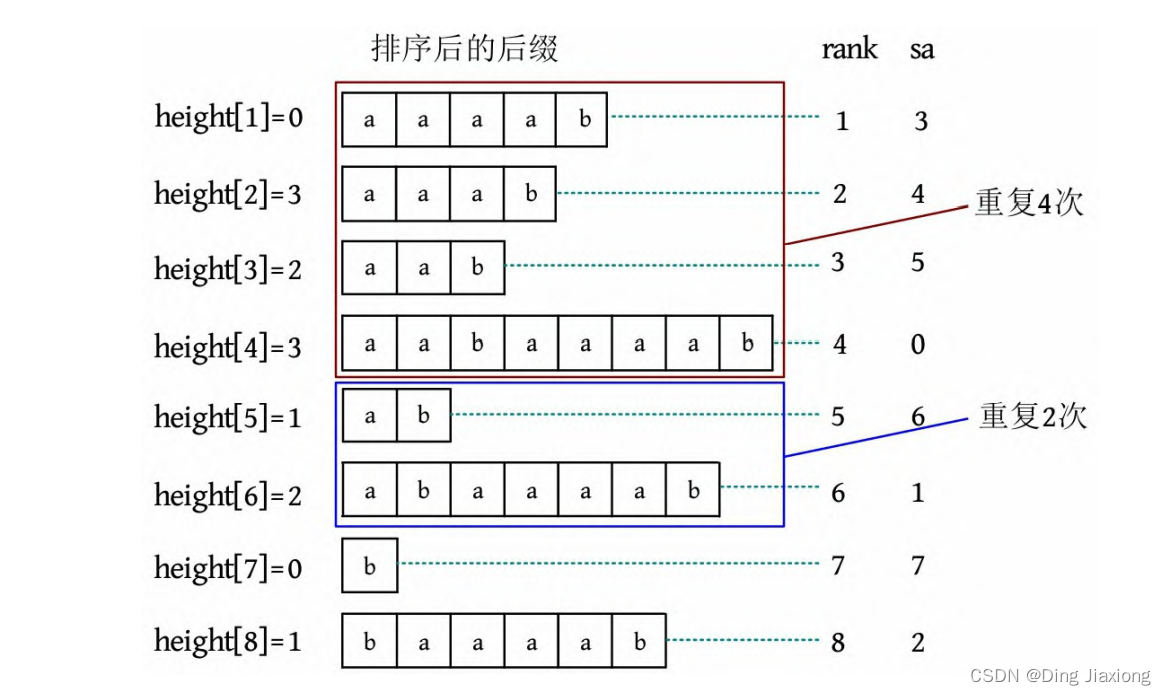
[2] 可重叠且重复k 次。给定一个字符串，求至少出现k 次的最长重复子串的长度，这k 个子串可以重叠。可以使用二分法，判断是否存在k 个长度为l 的子串相同，将最长公共子串长度大于l 的分为一组，查看每一组内的后缀个数是否大于k 。例如对于字符
串“aabaaaab”，求至少出现4次的最长重复子串长度，则将最长公共子串长度大于2的分组后，第1组正好重复4次，至少出现4次的最长重复子串长度为2。该算法的时间复杂度为O (n logn )。

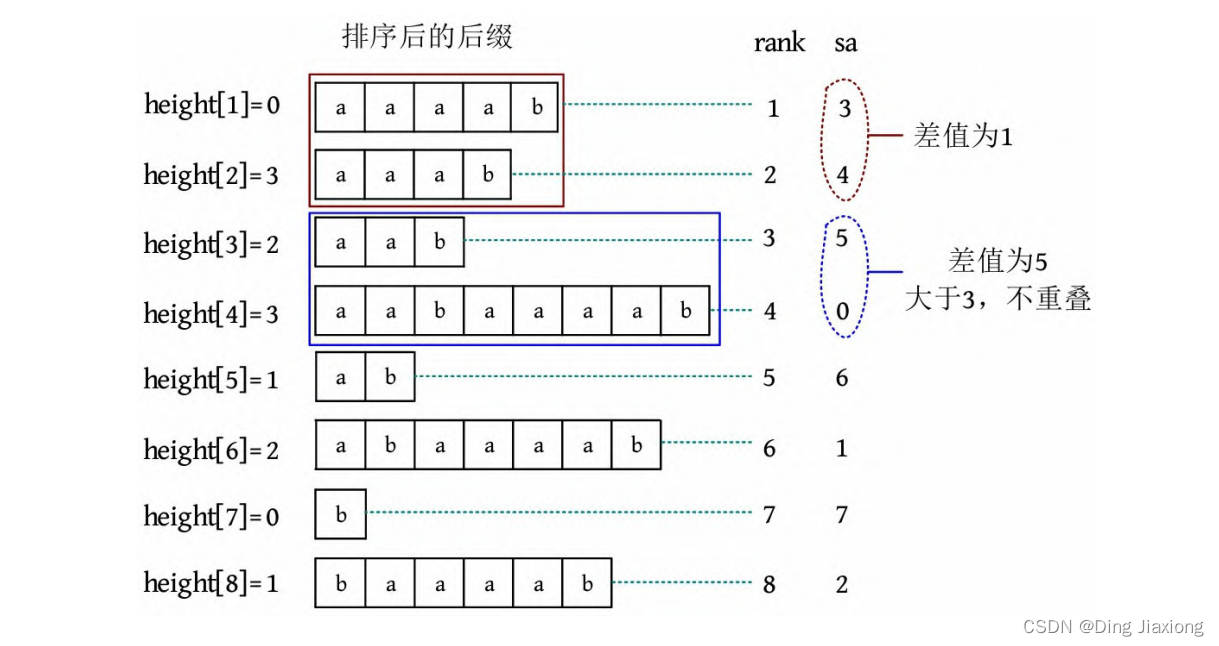
在这里插入图片描述

[3] 不可重叠。给定一个字符串，求最长重复子串的长度，这两个子串不可以重叠，可以使用二分法，判断是否存在两个长度为l 的子串相同，将最长公共子串长度大于l 的分为一组，查看每一组内后缀的sa最大值和最小值之差是否大于或等于l 。因为sa是后缀的开始下标，下标差值大于或等于l ，所以这两个后缀必然不重叠。例如，对于字符串“aabaaaab”，将最长公共子串长度大于3的分为一组：第1组，sa值之差为1，不满足条件；第2组，sa值之差为5，大于3，说明不重叠，满足条件。该算法的时间复杂度为O (n logn )。

在这里插入图片描述

(2) 不同子串的个数

给定一个字符串，求不同子串的个数。每个子串一定都是某个后缀的前缀，原问题转化为求所有后缀之间不同前缀的个数。对于每个sa[i]，累加n -sa[i ]-height[i ]即可得到答案，该算法的时间复杂度为O(n )。

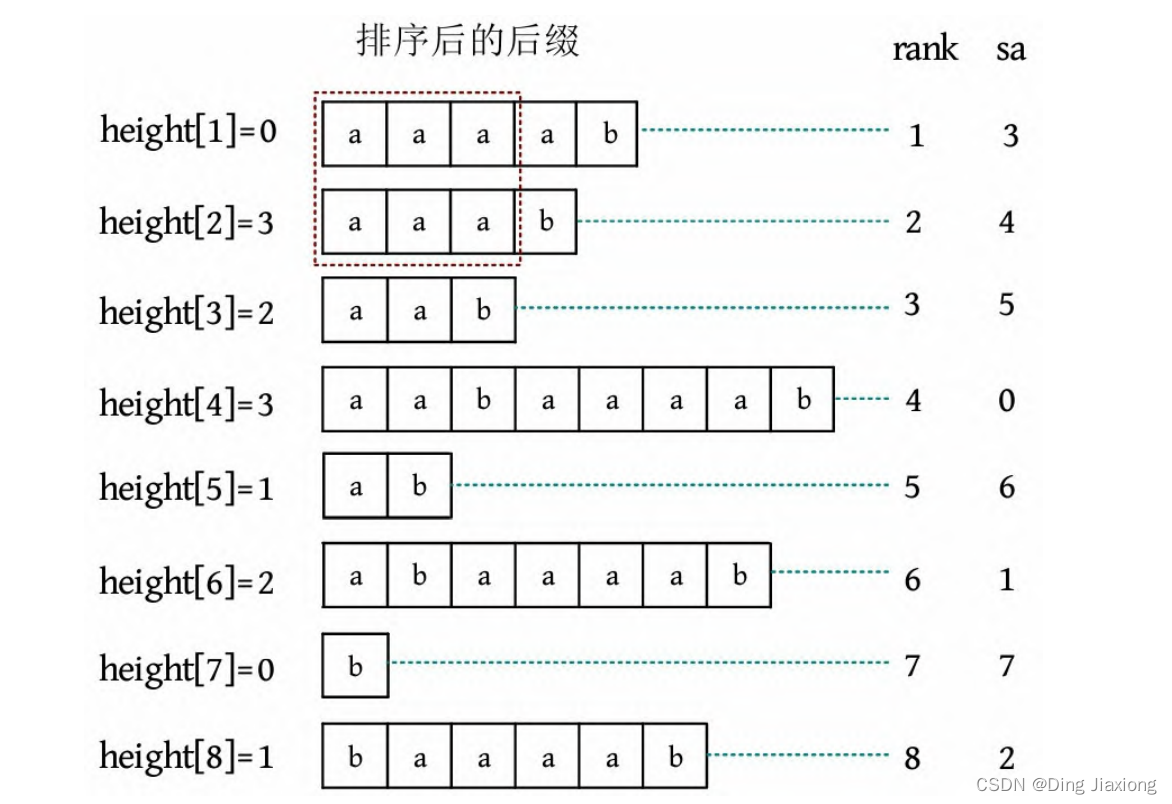
例如，对于字符串“aabaaaab”，求所有后缀之间不同前缀的个数，过程如下。

[1] sa[1]=3，即排名第1的后缀是从第3个字符开始的，该后缀为“aaaab”，其长度为n -sa[1]=5，将产生5个新的前缀：a、aa、aaa、aaaa、aaaab。

[2] sa[2]=4，将产生n -sa[2]个新的前缀，其中height[2]个前缀与前一个字符串的前缀重复，n -sa[2]-height[2]=8-4-3=1，因此将产生1个新的前缀。

[3] 对于sa[i ]，将产生n -sa[i ]-height[i ]个新的前缀，累加后即可得到所有不同前缀的个数。

在这里插入图片描述

(3) 最长回文子串

给定一个字符串，求最长回文子串的长度。可将字符串反过来连接在原字符串之后，中间用一个特殊的字符间隔，然后求这个字符串的后缀的最长公共前缀即可。该算法的时间复杂度为O (n logn )。例如，求字符串“xaabaay”的最长回文子串长度，首先将字符串反过来，用特殊字符“# ”间隔连接在原字符串之后为“xaabaay# yaabaax”，很快可以求出两个后缀“aabaay# yaabaax”“aabaax”的最长公共前缀长度为5，即最长回文子串的长度为5。

(4) 最长公共子串

对多个字符串，求重复k 次的最长公共子串，可以将每个字符串都用一个原字符串没有的特殊字符连接起来，然后求它们的最长公共前缀，求解时要判断是否属于不同的字符串。例如，求3个字符串“abcdefg”“bcdefgh”“cdefghi”至少重复两次的最长公共子串，可以用特殊字符“#”将3个字符串连接起来，得到“abcdefg#bcdefgh# cdefghi”，需要标记每个字符属于哪一个字符串，求解最长公共前缀。至少重复两次的最长公共子串为“bcdefg”“cdefgh”，后缀数组如下图所示。

在这里插入图片描述