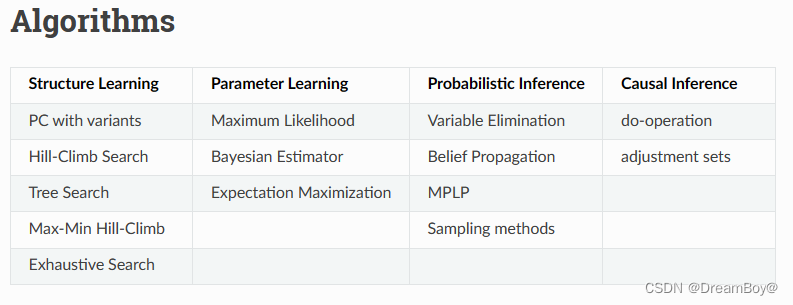
pgmpy

贝叶斯网络的纯python实现，
用途：

结构学习、
参数估计、
近似（基于采样）
精确推理
因果推理

安装

pip install pgmpy

conda install -c ankurankan pgmpy

conda install -c ankurankan pgmpy

文档

https://pgmpy.org/index.html

一、基础结构

1. DAG

图形中的每个节点都可以表示一个随机变量、因子或随机变量聚类。图中的边表示它们之间的依赖关系。

from pgmpy.base import DAG
G = DAG()

#添加点
'''add_node(node, weight=None, latent=False)'''
G.add_node(node='a')
'''add_nodes_from(nodes, weights=None, latent=False)'''
'''latent:无法直接观察到但可能对因果关系产生影响的未测量变量。'''
G.add_nodeslatent_from(nodes=['a', 'b'])
#添加边
'''add_edge(u, v, weight=None)'''
G.add_edge(u='a', v='b')
'''add_edges_from(ebunch, weights=None)'''
G.add_edges_from(ebunch=[('a', 'b'), ('b', 'c')]) #自动添加点中不存在的点

#查看节点，边
G.nodes()
NodeView(('Alice', 'Bob', 'Charles'))
G.edges()
OutEdgeView([('Alice', 'Bob')])

# check if node in graph
 'a' in G     
# number of nodes in graph  图中的节点数
len(G)  


#  遍历节点
'''active_trail_nodes(variables, observed=None, include_latents=False)'''
from pgmpy.base import DAG
G = DAG()
G.add_nodes_from(['A', 'B', 'C'])
G.add_edges_from([('A', 'B'),
                  ('E', 'B'),
                  ('B', 'D'),
                  ('D', 'C'),
                  ('D', 'F'),
                  ('D', 'H'),
                  ('D', 'G')])
G.active_trail_nodes(['A', 'B'], observed='G')

# 干预  去掉指向该节点的边
'''do(nodes, inplace=False)'''

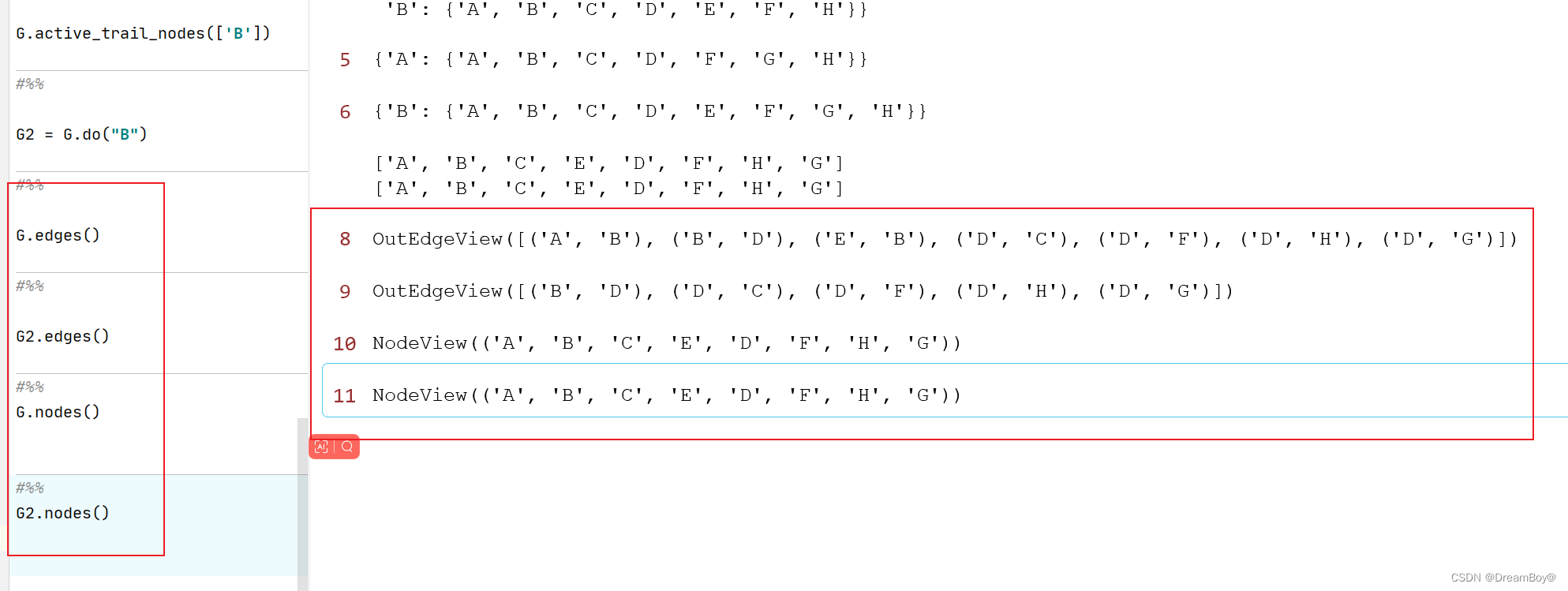
返回给定节点的祖先图。祖先图仅包含节点中至少一个变量的祖先节点。
'''get_ancestral_graph(nodes)'''

# 返回节点的子节点列表
'''get_children(node)'''

# 查找不可直接到达的节点
get_immoralities()

# 独立性检验
from pgmpy.base import DAG
chain = DAG([('X', 'Y'), ('Y', 'Z')])
chain.get_independencies()
(X ⟂ Z | Y)
(Z ⟂ X | Y)

# 叶子节点get_leaves()

# 节点的父项、子节点和子节点的其他父项的集合。
'''get_markov_blanket(node) '''

# 返回节点的父级列表。如果图形中不存在节点，则引发错误。
'''get_parents(node)[source]'''

#返回随机生成的 DAG，其中包含n_nodes个边概率为edge_prob的节点数。
'''get_random(n_nodes=5, edge_prob=0.5, latents=False)'''

# 返回图形根的列表。
'''get_roots()'''

如果观察到观察到的开始节点和结束节点之间存在活动跟踪（即 d 连接），则返回 True。
'''is_dconnected(start, end, observed=None)'''

# Checks whether the given model is I-equivalent 相同的图结构不同的边方向
'''is_iequivalent(model)'''

from pgmpy.base import DAG
G = DAG()
G.add_edges_from([('V', 'W'), ('W', 'X'),
                  ('X', 'Y'), ('Z', 'Y')])
G1 = DAG()
G1.add_edges_from([('W', 'V'), ('X', 'W'),
                   ('X', 'Y'), ('Z', 'Y')])
G.is_iequivalent(G1)
True

# 返回包含每个变量的局部独立性的独立实例。
''' local_independencies(variables)'''

#查找开始和结束的最小 d 分隔集。
'''minimal_dseparator(start, end)'''

#删除 DAG 中的所有不可到达边为并创建一个图
'''moralize()'''

# 可视化
https://docs.daft-pgm.org/en/latest/

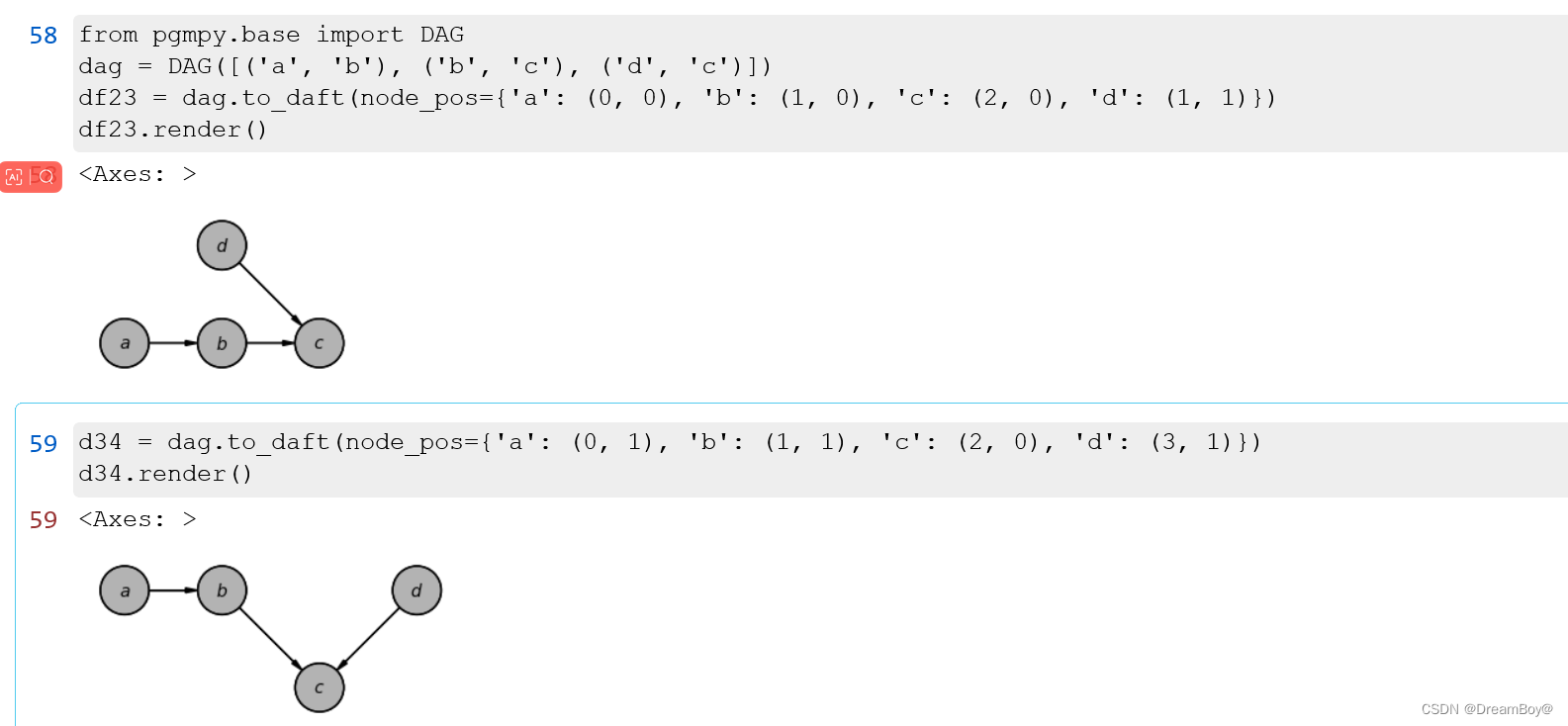
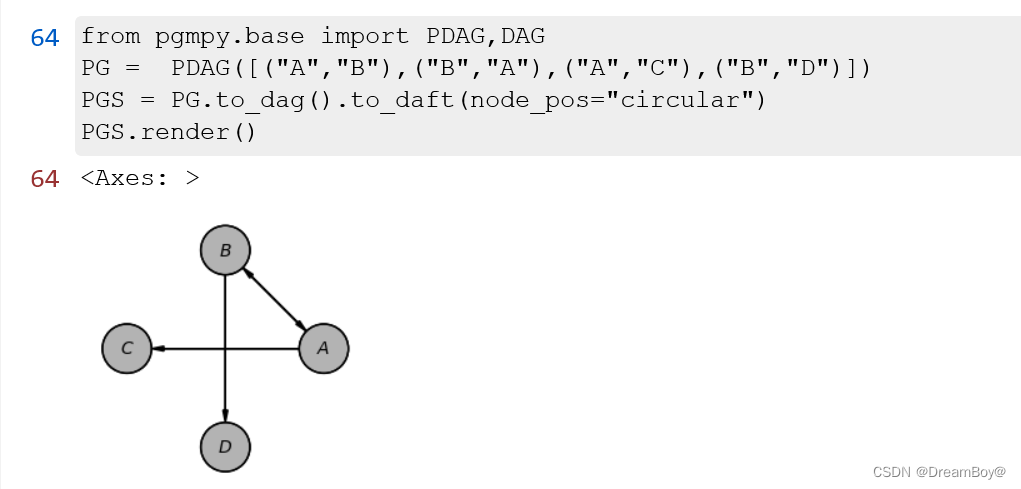
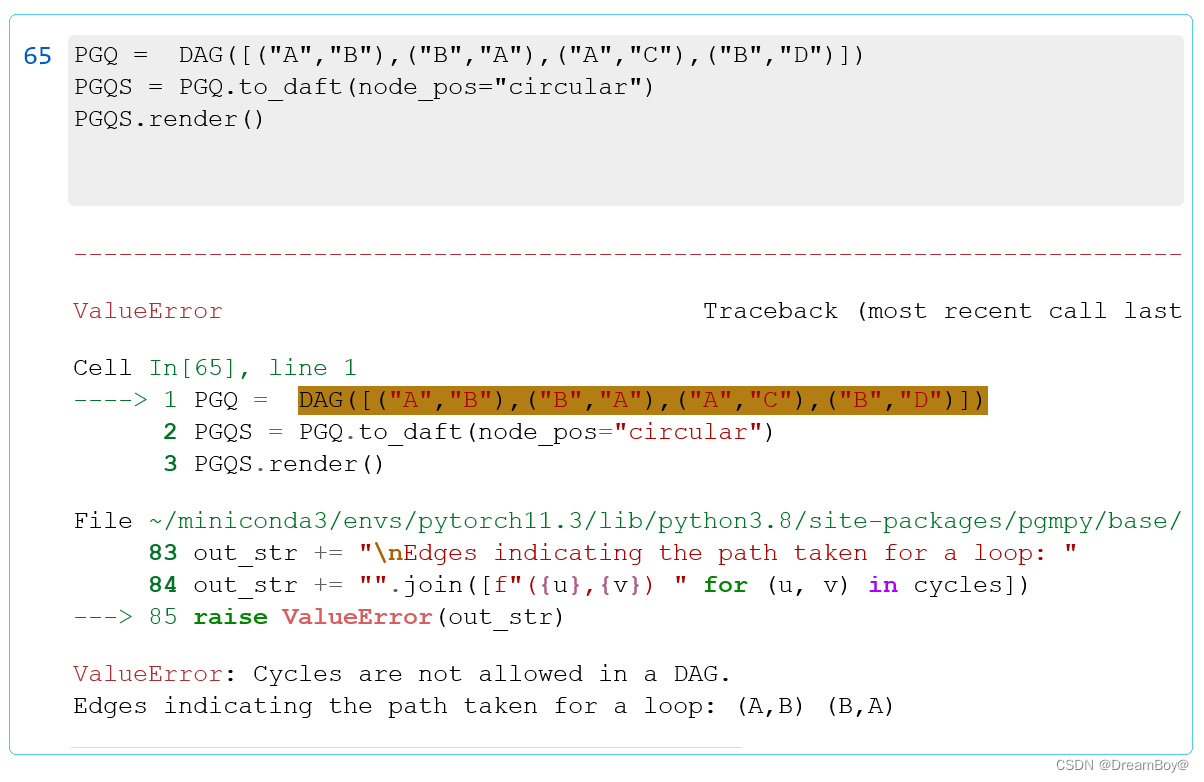
2. PDAG

用于表示 PDAG（也称为 CPDAG）的类。PDAG 是 DAG 的等效类，包含有向边和无向边。无向边在两个方向上使用两条边表示，即 X - Y 之间的无向边使用 X -> Y 和 X <- Y 表示。有环图用PDAG表示。

classpgmpy.base.PDAG(directed_ebunch=[], undirected_ebunch=[], latents=[])