其中代码均来自李沐老师的动手学pytorch中。

class PositionWiseFFN(nn.Module):
    '''
    ffn_num_inputs 4
    ffn_num_hiddens 4
    ffn_num_outputs 8
    '''
    def __init__(self,ffn_num_inputs,ffn_num_hiddens,ffn_num_outputs):
        super(PositionWiseFFN,self).__init__()
        self.dense1 = nn.Linear(ffn_num_inputs,ffn_num_hiddens)#4*4
        self.relu = nn.ReLU()
        self.dense2 = nn.Linear(ffn_num_hiddens,ffn_num_outputs)#4*8
    def forward(self,X):
        return self.dense2(self.relu(self.dense1(X)))
positionWiseFFN = PositionWiseFFN(4,4,8)
positionWiseFFN.eval()
positionWiseFFN(torch.ones(size=(2,3,4)))[0]

上面的代码为前馈神经网络结构，其实也就是一个全连接层。

class AddNorm(nn.Module):
    def __init__(self,normalized_shape,dropout):
        super(AddNorm, self).__init__()
        self.dropout=nn.Dropout(dropout)
        self.layer_norm=nn.LayerNorm(normalized_shape=normalized_shape)
    def forward(self,x,y):
        return self.layer_norm(self.dropout(y)+x)
#比如[3, 4]或torch.Size([3, 4])，则会对网络最后的两维进行归一化，且要求输入数据的最后两维尺寸也是[3, 4]
add_norm = AddNorm(normalized_shape=[3,4],dropout=0.5)
add_norm.eval()
add_norm(torch.ones(size=(2,3,4)),torch.ones(size=(2,3,4)))

这里实现的是残差化和规范化。nn.LayerNorm(normalized_shape=normalized_shape)为layer规范化，其中normalized_shape为[3, 4]，对网络最后的两维进行归一化。

class MultiHeadAttention(nn.Module):
    def __init__(self,query_size,key_size,value_size,num_hiddens,num_heads,dropout,bias=False):
        super(MultiHeadAttention, self).__init__()
        self.num_heads=num_heads
        #用独立学习得到的 ℎ 组不同的线性投影（linear projections）来变换查询、键和值
        self.attention=d2l.torch.DotProductAttention(dropout)
        self.W_q=nn.Linear(query_size,num_hiddens,bias=bias)
        self.W_k=nn.Linear(key_size,num_hiddens,bias=bias)
        self.W_v = nn.Linear(value_size, num_hiddens, bias=bias)
        self.W_o = nn.Linear(num_hiddens, num_hiddens, bias=bias)
#总之就是：我们的Q，K，V的embedding，怎么拆分成k个头的数据，然后放到一个大头中，一遍算出multi_head的值
#这里是一组QKV乘一组W 直接生成特征大小的结果，在切分成8份，放到batch里等价于并行计算
    def forward(self,queries,keys,values,valid_lens):
        # print('----')
        # print(queries)
        queries = transpose_qkv(self.W_q(queries),self.num_heads)
        # print(queries)
        # print('----')
        keys = transpose_qkv(self.W_k(keys),self.num_heads)
        values = transpose_qkv(self.W_v(values),self.num_heads)
        if valid_lens is not None:
            # 在轴0，将第一项（标量或者矢量）复制num_heads次，
            # 然后如此复制第二项，然后诸如此类。
            valid_lens = torch.repeat_interleave(valid_lens,repeats=self.num_heads,dim=0)
        #valid_lens tensor([3, 3, 3, 3, 3, 2, 2, 2, 2, 2])
        # output的形状:(batch_size*num_heads，查询的个数，
        # num_hiddens/num_heads)
        # print(queries.shape)
        # print(keys.shape)
        '''
        queries-->torch.Size([10, 4, 20])
        keys----->torch.Size([10, 6, 20])
        两个批次，每次五个多头注意力，就一共会有十个注意力需要做。得出的矩阵为10*4*6，表示为10次注意力
        每个注意力query和key的矩阵为4*6
              keys  keys  keys  keys  keys  keys
        Query
        Query
        Query
        Query
        在经过mask时 需要将10*4*6的矩阵，转为二维矩阵，就是40*6。
        valid_lens首先会在上面的代码中，扩展至num_heads，然后会在masked_softmax中扩至40大小。
        
        '''
        output = self.attention(queries,keys,values,valid_lens)
        # print('-----')
        # print(output)
        # print('-----')
        # output_concat的形状:(batch_size，查询的个数，num_hiddens)
        output_concat = transpose_output(output,self.num_heads)
       # print(output_concat.shape)torch.Size([2, 4, 100])
        return self.W_o(output_concat)
def transpose_qkv(X,num_heads):
    # 2,6,100 2,4,100
    X = X.reshape(X.shape[0],X.shape[1],num_heads,-1)
    # 2,5,6,20  2,5,4,20
    # 输出X的形状: (batch_size，num_heads，查询或者“键－值”对的个数, num_hiddens/num_heads)
    X = X.permute(0, 2, 1, 3)
    #最终输出的形状: (batch_size * num_heads,查询或者“键－值”对的个数,num_hiddens/num_heads)
    #10,6,20  10,6,20
    return X.reshape(-1, X.shape[2], X.shape[3])
def transpose_output(X,num_heads):
    """逆转transpose_qkv函数的操作"""
    X = X.reshape(-1,num_heads,X.shape[1],X.shape[2])
    X = X.permute(0,2,1,3)
    return X.reshape(X.shape[0],X.shape[1],-1)
#在这里，我们设置head为5，也就是一共有5次self-attention。
num_hiddens,num_heads = 100,5
multiHeadAttention = MultiHeadAttention(num_hiddens,num_hiddens,num_hiddens,num_hiddens,5,0.5)
multiHeadAttention.eval()

batch_size,num_queries = 2,4
num_kvpairs,valid_lens = 6,torch.tensor([3,2])
#2,6,100 批次 句子长度 embedsize
Y = torch.ones(size=(batch_size,num_kvpairs,num_hiddens))
#2,4,100
X = torch.ones(size=(batch_size,num_queries,num_hiddens))
print(multiHeadAttention(X,Y,Y,valid_lens).shape)

首先我们设置head为5。num_hiddens可以理解为query或者key的大小，num_kvpairs表示每次注意力中key的数量，num_queries表示每次注意力中query的数量。value的数量与key的数量一样。另外一种理解就是，将X理解为批次*句子长度(单词的数量)*embedding size。每个单词对应一次查询。随后就是__init__，创建几个全连接层，对query、key、value进行变换，不同注意力的query、key和value，均不一样。

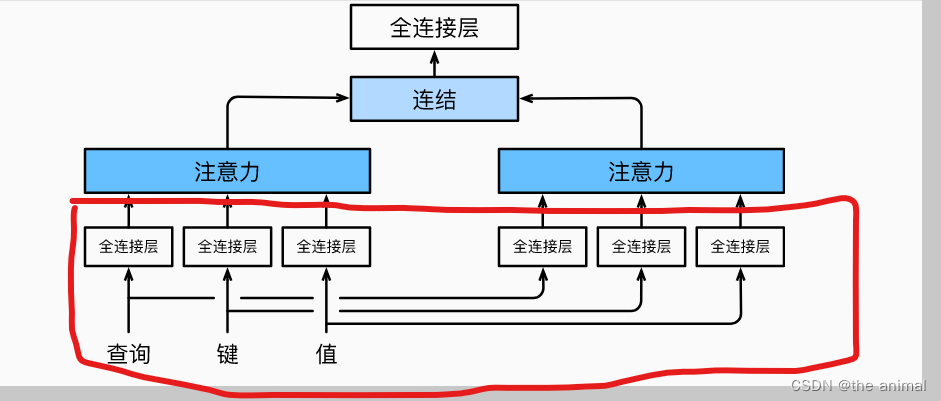
主要是实现图中红色部分。然后会调用forward函数，transpose_qkv函数进行切分，假定原本的输入为2 * 6 * 100，因为大小为两个批次，每个批次需要做五个注意力机制，每个注意力机制的key的数量为6，所以将输入为2 * 6 * 100，转换为10 * 6 * 20。意思就是10次注意力，每个注意力中的key为6个，每个key由20维度的向量表示。query同理。因为我们要并行计算，这样使用torch.bmm可以直接进行计算，计算得出Query和key矩阵。在上面的例子中，计算得出的为10 * 4 * 6大小的矩阵。
在训练时刻的mask中，首先会将结果转变为二维矩阵40 * 6，其中的每一行代表了query与不同key计算的结果，有时候query只能和部分key进行计算，比如：第二个词的query只能计算第一个词与第二个词的key，而之后key需要进行mask。我们会给定一个valid_lens 代表需要保留的计算结果。其中mask部分会调用以下代码：

 mask = torch.arange((maxlen), dtype=torch.float32,device=X.device)[None, :] < valid_len[:, None]
 X[~mask] = value#value为极小值。

torch.arange((maxlen)会生成从0到5的矩阵，valid_len在之前会经过扩展为140大小的矩阵，然后转换为40 * 1的矩阵。最终的mask会变成40 * 6大小矩阵就像以下形式：
[True,True,True,False,False]
而最后两个False是需要进行mask的，X[~mask] = value将最后两个Fasle，变为负极小值，再经过softmax之后，结果将趋近于0，从而将其mask。然后与value相乘，得出结果为10 * 4 20矩阵大小的结果，在经过变换，变为2 * 4* 100矩阵，最后再经过最后一次全连接层，然后输出结果。