文章目录
- 一:概述
- (1)什么是随机化算法
- (2)随机化算法的特点
- (3)随机化算法分类
- (4)随机数
- 二:数值随机化算法(以计算 π π π值为例)
- 三:舍伍德算法(以快速排序为例)
- 四:拉斯维加斯算法(以N皇后问题为例)
- (1)拉斯维加斯算法概述
- (2)N皇后问题
- A:问题概述
- B:回溯算法解决N皇后问题
- C:拉斯维加斯算法解决N皇后问题
- 五:蒙特卡罗算法(以主元素问题为例)
一:概述
(1)什么是随机化算法
随机化算法:随机化算法把“对于所有合理的输入都必须给出正确的输出”这一求解问题的条件放宽,将随机性选择注入到算法中,在算法执行某些步骤时,可以随机地选择下一步该如何进行,同时允许结果是近似解或以较小概率出现错误,并以此为代价,获得算法运行时间的大幅度减少。随机化算法执行中注入的随机性依赖于随机数发生器所产生的随机数
(2)随机化算法的特点
随机化特点:
- 允许算法执行过程中随机选择下一计算步骤。
- 当算法执行过程中面临选择时,随机化算法通常比最优选择算法省时。可在很大程度上降低算法复杂性
- 对所求问题的同一实 用同一随机化算法求解两次,两次求解所需的时间甚至所得的结果可能有相当大的差别
- 设计思想简单,易于实现
(3)随机化算法分类
随机化算法分类:
- 数值随机算法
- 舍伍德算法
- 拉斯维加斯算法
- 蒙特卡罗算法
(4)随机数
随机数:随机数在随机化算法设计中扮演着十分重要的角色,但计算机无法产生真正的随机数,在随机化算法中使用的随机数都是伪随机数,其中线性同余法是产生伪随机数的最常用的方法
二:数值随机化算法(以计算 π π π值为例)
数值随机化算法:将一个问题的计算与某已经确定的概率分布的事件联系起来,算法求解结果一般为近似解,注意
- 解精度随计算时间的增加而提高
- 某些情况下计算问题的精确解是不可能或没必要
以计算 π π π值问题为例:设有一半径为 r r r的圆及其外切四边形。向该正方形随机地投掷 n n n个点。设落入圆内的点数为 k k k。若所投入的点在正方形上满足均匀分布,则所投入的点落入圆内的概率可由下式计算:
π r 2 4 r 2 = π 4 ≈ k n \frac{πr^{2}}{4r^{2}}=\frac{π}{4}\approx \frac{k}{n} 4r2πr2=4π≈nk
当 n n n足够大时, k k k与 n n n之比近似逼近这一概率,从而有:
π ≈ 4 k n π\approx\frac{4k}{n} π≈n4k
代码如下
#include <iostream>
#include <cstdlib>
using namespace std;
// 获得0-1之间的随机数
double get_random_num ()
{
return (double)rand() / RAND_MAX ;
}
// 用随机投点法计算 PI
double darts (int n)
{
int k = 0 ;
for (int i = 0; i < n; ++ i) {
// 投掷n个点,随机生成点(x, y)
double x = get_random_num() ;
double y = get_random_num() ;
//如果该点落在圆内,则k++
if ((x * x + y * y) <= 1.0) {
++ k ;
}
}
//计算公式
return (4 * k) / (double)n ;
}
int main()
{
cout << darts (200000000) << endl ;
}

三:舍伍德算法(以快速排序为例)
舍伍德算法:当一个确定性算法在最坏情况下的计算复杂度与其在平均情况下的计算复杂度相差较大时,可以在该确定性算法中引入随机性将它改造为一个舍伍德算法,用来消除或减少问题不同实例之间在计算时间上的差别,舍伍德算法总能求得问题的正确解,具体方法为数据洗牌+确定算法
以快速排序为例:快速排序是基于分治策略的一个典型代表算法,其基本思想是对于输入的子数组a[p:r],按以下三个步骤进行排序
- 分解:以
a[p]为基准元素将a[p:r]划分成3段a[p:q-1]、a[q]和a[q+1:r],使a[p:q-1]中任一元素小于等于a[q],而a[q+1:r]中任一元素大于等于a[q]。下标q在划分过程中确定 - 递归求解:通过递归调用快速排序算法,分别对
a[p:q-1]和a[q+1:r]进行排序 - 合并:由于对
a[p:q-1]和a[q+1:r]的排序是就地进行的,因此在a[p:q-1]和a[q+1:r]都已排好序后,不需要执行任何计算,a[p:r]就已经排好序了
代码如下
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int Partition(vector<int>& data, int begin, int end){
int key = data[begin];//以左侧元素为基准元素
int save = begin;
while(begin < end){
while(begin < end && data[end] >= key){
//end处元素应该大于等于key,一旦找到小于key的就停止
--end;
}
while(begin < end && data[begin] <= key){
//end处元素应该小于等于key,一旦找到大于key的就停止
++begin;
}
swap(data[begin], data[end]);//交换
}
swap(data[save], data[end]);//让基准元素到"中间";
return begin;
}
void quickSort(vector<int>& data, int left, int right){
if(left < right){
int div = Partition(data, left, right);
quickSort(data, left, div-1);
quickSort(data, div+1, right);
}else{
return;
}
}
void print(vector<int>& data){
for(int i = 0; i < data.size(); i++){
cout << data[i] << " ";
}
cout << endl;
}
int main(){
vector<int> test = {21, 43, 32, 18, 29, 30, 21, 55, 43, 17, 83};
print(test);
quickSort(test, 0, test.size());
print(test);
return 0;
}

快速排序算法的核心在于合适的划分基准,这个划分基准将直接导致划分的对称性,继而影响算法的性能。一旦基准挑选的不合理,如下图,那么将导致算法时间复杂度非常高
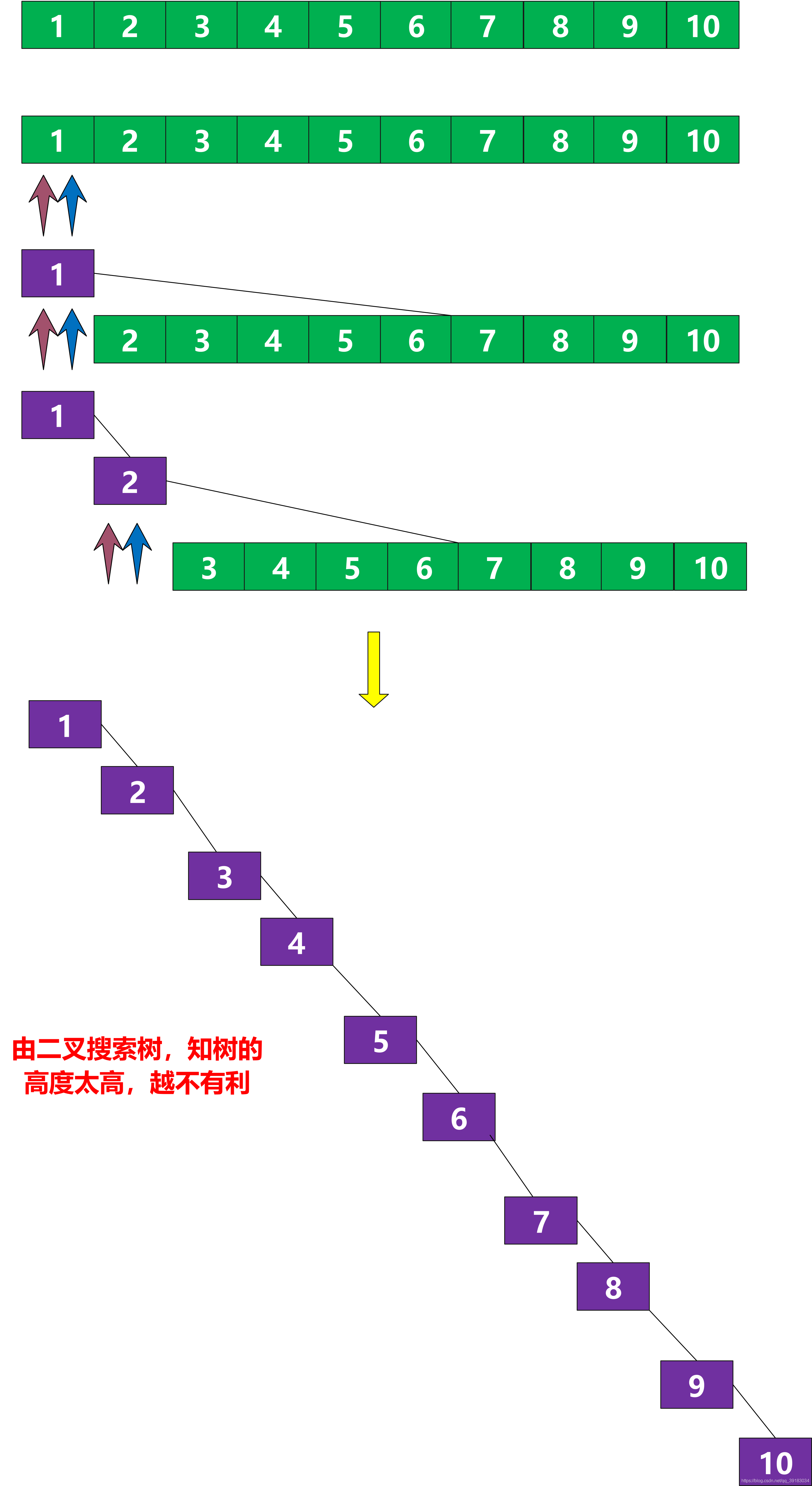
因此,舍伍德算法通过采用随机选择策略来随机选取出一个元素作为划分基准,这样可以使划分基准是随机的,从而可以期望划分是较为对称的
代码如下
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int Partition(vector<int>& data, int begin, int end){
// 随机挑选
int rand_idx = (rand() % (end - begin +1)) + begin;
swap(data[begin], data[rand_idx]);
int key = data[begin];//以左侧元素为基准元素
int save = begin;
while(begin < end){
while(begin < end && data[end] >= key){
//end处元素应该大于等于key,一旦找到小于key的就停止
--end;
}
while(begin < end && data[begin] <= key){
//end处元素应该小于等于key,一旦找到大于key的就停止
++begin;
}
swap(data[begin], data[end]);//交换
}
swap(data[save], data[end]);//让基准元素到"中间";
return begin;
}
void quickSort(vector<int>& data, int left, int right){
if(left < right){
int div = Partition(data, left, right);
quickSort(data, left, div-1);
quickSort(data, div+1, right);
}else{
return;
}
}
void print(vector<int>& data){
for(int i = 0; i < data.size(); i++){
cout << data[i] << " ";
}
cout << endl;
}
int main(){
vector<int> test = {21, 43, 32, 18, 29, 30, 21, 55, 43, 17, 83};
print(test);
quickSort(test, 0, test.size());
print(test);
return 0;
}

四:拉斯维加斯算法(以N皇后问题为例)
(1)拉斯维加斯算法概述
拉斯维加斯算法:舍伍德型算法的优点是,其计算时间复杂性对所有实例而言相对均匀,但与其相应的确定性算法相比,其平均时间复杂性没有改进。拉斯维加斯算法则不然,它能显著地改进算法的有效性,甚至对某些迄今为止找不到有效算法的问题,也能得到满意的结果。具体来说
-
拉斯维加斯算法求得的解总是正确的,求解中算法所作的随机性决策有可能导致算法找不到所需的解
-
一般情况下,求得正确解的概率随计算时间增加而增大
-
对同一实例,重复执行一个拉斯维加斯算法,可使求解失败概率任意小
-
由于拉斯维加斯型算法有时运行成功,有时运行失败,故通常拉斯维加斯型算法的返回类型为
bool -
拉斯维加斯算法运行一次,或者得到一个正确的解,或者无解。因此,需要对同一输入实例反复多次运行算法,直到成功地获得问题的解
算法有两个参数
- 算法输入
- 当算法运行成功时保存问题的解
拉斯维加斯算法典型调用形式如下
void obstinate(Object x, Object y){
//反复调用拉斯维加斯算法直到找到问题的一个解y
bool success = false;
while(!success) success = lv(x, y)
}
(2)N皇后问题
A:问题概述
N皇后问题:在 n × n n×n n×n格的棋盘上放置彼此不相互攻击的 N N N个皇后。按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。N皇后问题等价于在 n × n n×n n×n格的棋盘上放置 N N N个皇后,任何2个皇后不能放在同一行或同一列或同一斜线上
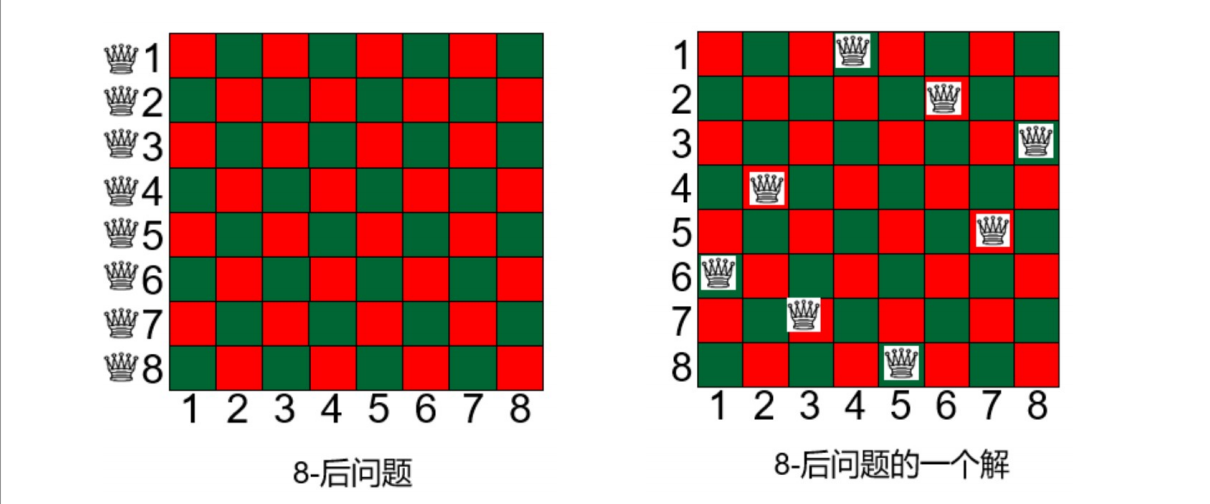
B:回溯算法解决N皇后问题
- 1
C:拉斯维加斯算法解决N皇后问题
在棋盘上相继各行中随机地放置皇后,使新放置皇后与已放置皇后互不攻击,直至 n n n个皇后均已相容地放置好,或没有下一个皇后的可放置位置时为止
- 注意:完全使用拉斯维加斯算法可能复杂度太高,长时间得不到解,所以下面的示例中前 t t t个皇后的位置由拉斯维加斯算法产生,后 N − t N-t N−t个皇后位置由回溯法产生
#include <iostream>
#include "Random.h"
#include <cmath>
#define MAX_V 100
using namespace std;
/* 判断某行放置皇后是否合法
* i : 即将放置的行数
* j : 即将放置的列数
* */
bool place(int map[MAX_V][MAX_V], int n, int i, int j){
for(int a = i - 1, b = 1; a >= 0; a--, b++){
//判断直线方向
if(map[a][j] == 1){
return false;
}
int l = j - b;
int r = j + b;
//判断两个斜线方向
if(l >= 0 && map[a][l] == 1){
return false;
}
if(r < n && map[a][r] == 1){
return false;
}
}
return true;
}
/* 回溯剩下的皇后位置
* t : 回溯开始的位置
* */
bool recall(int map[MAX_V][MAX_V], int n, int t){
if(t == n){
return true;
}
for(int i = 0; i < n; i++){
if(!place(map, n, t, i)){
continue;
}
map[t][i] = 1;
if(recall(map, n, t+1)){
return true;
}
map[t][i] = 0;
}
return false;
}
/* n 皇后问题
* map : 棋盘
* n : 棋盘大小
* t : 使用拉斯维加斯算法的层次数
* */
void nQueen(int map[MAX_V][MAX_V], int n, int t){
Random rand;
int i;
while(i != n){ //循环调用,直到产生解
for(i = 0; i < t; i++){
int randPos = rand.rand(n); //产生[0, n)的随机数
if(!place(map, n, i, randPos)){
break;
}
for(int j = 0; j < n; j++){
map[i][j] = 0;
}
map[i][randPos] = 1;
}
if(i == t && recall(map, n, t)){
i = n;
}
}
}
int main(){
int map[MAX_V][MAX_V] = {0};
nQueen(map, 10, 7);
for(int i = 0; i < 10; i++){
for(int j = 0; j < 10; j++){
cout << map[i][j] << " ";
}
cout << endl;
}
return 0;
}
五:蒙特卡罗算法(以主元素问题为例)
拉斯维加斯算法:蒙特卡罗方法又称随机抽样或统计试验方法。传统的经验方法由于不能逼近真实的物理过程,很难得到满意的结果,而蒙特卡罗方法由于能够真实地模拟实际物理过程,故解决问题与实际非常符合,可以得到很圆满的结果。 在实际应用中常会遇到一些问题,不论采用确定性算法或随机化算法都无法保证每次都能得到正确的解答。蒙特卡罗算法则在一般情况下可以保证对问题的所有实例都以高概率给出正确解,但是通常无法判定一个具体解是否正确。蒙特卡罗算法一般包含如下三个步骤
- 构造随机的概率过程:对于本身就具有随机性质的问题,要正确描述和模拟这个概率过程。对于本来不是随机性质的确定性问题,比如计算定积分,就必须事先构造一个人为的概率过程了(例如最开始的圆周率 π \pi π的求解)
- 从已知概率分布抽样:由于各种概率模型都可以看作是由各种各样的概率分布构成的,因此产生已知概率分布的随机变量,就成为实现蒙特卡罗方法模拟实验的基本手段
- 求解估计量:实现模拟实验后,要确定一个随机变量,作为所要求问题的解,即无偏估计。建立估计量,相当于对实验结果进行考察,从而得到问题的解
以主元素问题为例:设 T [ n ] T[n] T[n]是含有 n n n个元素的数组, x x x是该数组的一个元素,如果数组中有一半以上的元素与 x x x相同,则称元素 x x x为数组 T T T的主元素
- 例如:数组 T = { 3 , 2 , 3 , 2 , 3 , 3 , 5 } T=\{3, 2, 3, 2, 3, 3, 5\} T={3,2,3,2,3,3,5}中元素3的就是主元素
蒙特卡罗解决思路:随机选择数组中的一个元素
T
[
i
]
T[i]
T[i]进行统计,如果该元素出现的次数大于
n
2
\frac{n}{2}
2n,则该元素就是数组的主元素,算法返回true,否则该元素不是主元素,返回false。如果数组中存在主元素,则非主元素个数小于
n
2
\frac{n}{2}
2n,因此该算法将会以大于
1
2
\frac{1}{2}
21的概率返回true,以小于
1
2
\frac{1}{2}
21的概率返回false,这说明算法出现找不到正确解的概率小于
1
2
\frac{1}{2}
21。如果连续调用算法
k
k
k次,算法返回false的概率将减少为
2
−
k
2^{-k}
2−k
代码如下
//随机化算法 蒙特卡罗算法 主元素问题
#include "stdafx.h"
#include "RandomNumber.h"
#include <cmath>
#include <iostream>
using namespace std;
//判定主元素的蒙特卡罗算法
template<class Type>
bool Majority(Type *T,int n)
{
RandomNumber rnd;
int i = rnd.Random(n);
Type x = T[i]; //随机选择数组元素
int k = 0;
for(int j=0; j<n; j++)
{
if(T[j] == x)
{
k++;
}
}
return (k>n/2); //k>n/2时,T含有主元素
}
//重复k次调用算法Majority
template<class Type>
bool MajorityMC(Type *T,int n,double e)
{
int k = ceil(log(1/e)/log((float)2));
for(int i=1; i<=k; i++)
{
if(Majority(T,n))
{
return true;
}
}
return false;
}
int main()
{
int n = 10;
float e = 0.001;
int a[] = {5,5,5,5,5,5,1,3,4,6};
cout<<"数组a的元素如下:"<<endl;
for(int i=0; i<10; i++)
{
cout<<a[i]<<" ";
}
cout<<endl;
cout<<"调用MajorityMC判断数组是否含有主元素结果是:"<<MajorityMC(a,n,e)<<endl;
}