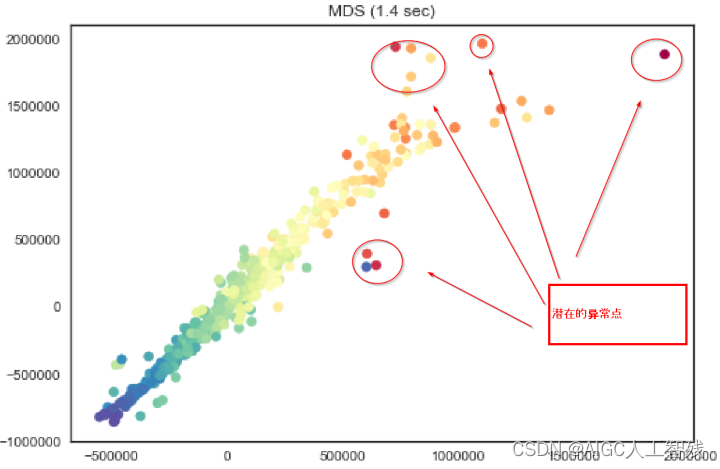
异常点检测(Outlier detection)，⼜称为离群点检测，是找出与预期对象的⾏为差异较⼤的对象的⼀个检测过程。这些被检测出的对象被称为异常点或者离群点。异常点（outlier）是⼀个数据对象，它明显不同于其他的数据对象。异常点检测的应用也十分广泛，例如：信用卡反欺诈、工业损毁检测、广告点击反作弊、刷单检测和羊毛党检测等等。
一般异常检测是无监督学习，因为它不是二分类而是多分类问题。

**问题1：**为什么要用无监督异常检测方法？

很多场景没有标签或者标签很少，不能进行监督训练；而且样本总是在发生变化。

目前主流的异常检测方法的基本原理都是基于样本间的相似度：距离、密度、角度、隔离所需的难度和簇等等。

常见的异常检测有：

• Z-Score检验——统计学方法
• Local Outlier Factor
• 孤立森林

Z-Score检验

通过ZScore将正态分布的数据转化为标准正态分布数据，公式下：
$$Zscore=\frac{(x-u)}{\sigma }$$

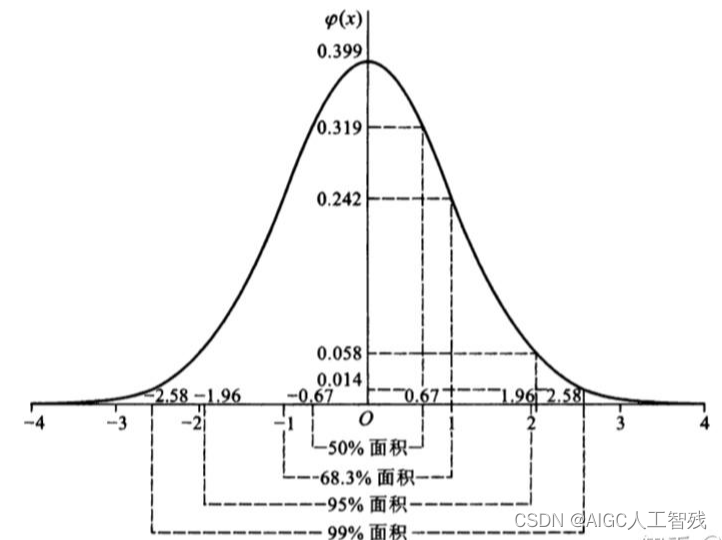
如果符合正态分布，则有68%的数据在±$\sigma$之间；95%的数据在±2$\sigma$之间；有99.7%的数据在±3$\sigma$之间。
但大部分场景的数据都不满足正态分布的数据。

Local Outlier Factor(LOF算法)

LOF算法是基于密度的异常检测算法，它会为每个数据点计算一个分数，通过分数的大小来判断数据是否异常。
LOF算法的流程如下：
1）⾸先对样本空间进⾏去重，分别计算每⼀个样本到样本空间内其余点的距离。
2）将步骤1中的距离升序排列。
3）指定近邻样本个数k，对于每个样本点，寻找其k近邻样本，然后计算LOF分数，作为异常分数。

LOF例子

还是以评分卡模型数据为例。

from pyod.models.lof import LOF
import pandas as pd
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import roc_auc_score,roc_curve,auc,recall_score

data = pd.read_csv('Bcard.txt')
feature_lst = ['person_info','finance_info','credit_info','act_info']
# 划分数据
train = data[data.obs_mth != '2018-11-30'].reset_index().copy()
val = data[data.obs_mth == '2018-11-30'].reset_index().copy()
x = train[feature_lst]
y = train['bad_ind']
# 使用lof进行异常点检测
lof_clf = LOF(n_neighbors=20,algorithm='auto')
lof_clf.fit(x)
out_pred = lof_clf.predict_proba(x)[:,1]
train['out_pred'] = out_pred
# 确定得分边界值
key = train['out_pred'].quantile(0.95)
lof_x = train[train.out_pred<key][feature_lst]
lof_y = train[train.out_pred<key]['bad_ind']
val_x = val[feature_lst]
val_y = val['bad_ind']

# 训练模型
lr_model = LogisticRegression(C=0.1,class_weight='balanced')
lr_model.fit(lof_x,lof_y)

# 训练集
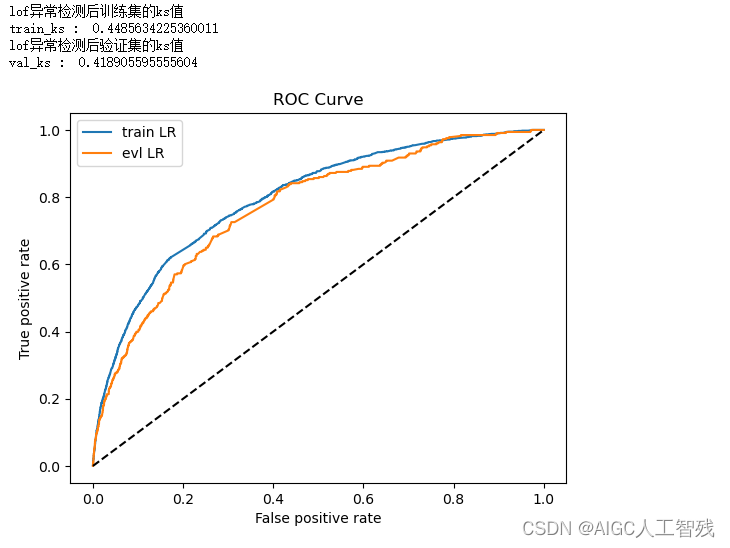
print('lof异常检测后训练集的ks值')
y_pred = lr_model.predict_proba(lof_x)[:,1] #取出训练集预测值
fpr_lr_train,tpr_lr_train,_ = roc_curve(lof_y,y_pred) #计算TPR和FPR
train_ks = abs(fpr_lr_train - tpr_lr_train).max() #计算训练集KS
print('train_ks : ',train_ks)

#验证集
y_pred = lr_model.predict_proba(val_x)[:,1] #计算验证集预测值
fpr_lr,tpr_lr,_ = roc_curve(val_y,y_pred) #计算验证集预测值
val_ks = abs(fpr_lr - tpr_lr).max() #计算验证集KS值
print('lof异常检测后验证集的ks值')
print('val_ks : ',val_ks)

from matplotlib import pyplot as plt
plt.plot(fpr_lr_train,tpr_lr_train,label = 'train LR')
plt.plot(fpr_lr,tpr_lr,label = 'evl LR')
plt.plot([0,1],[0,1],'k--')
plt.xlabel('False positive rate')
plt.ylabel('True positive rate')
plt.title('ROC Curve')
plt.legend(loc = 'best')
plt.show()

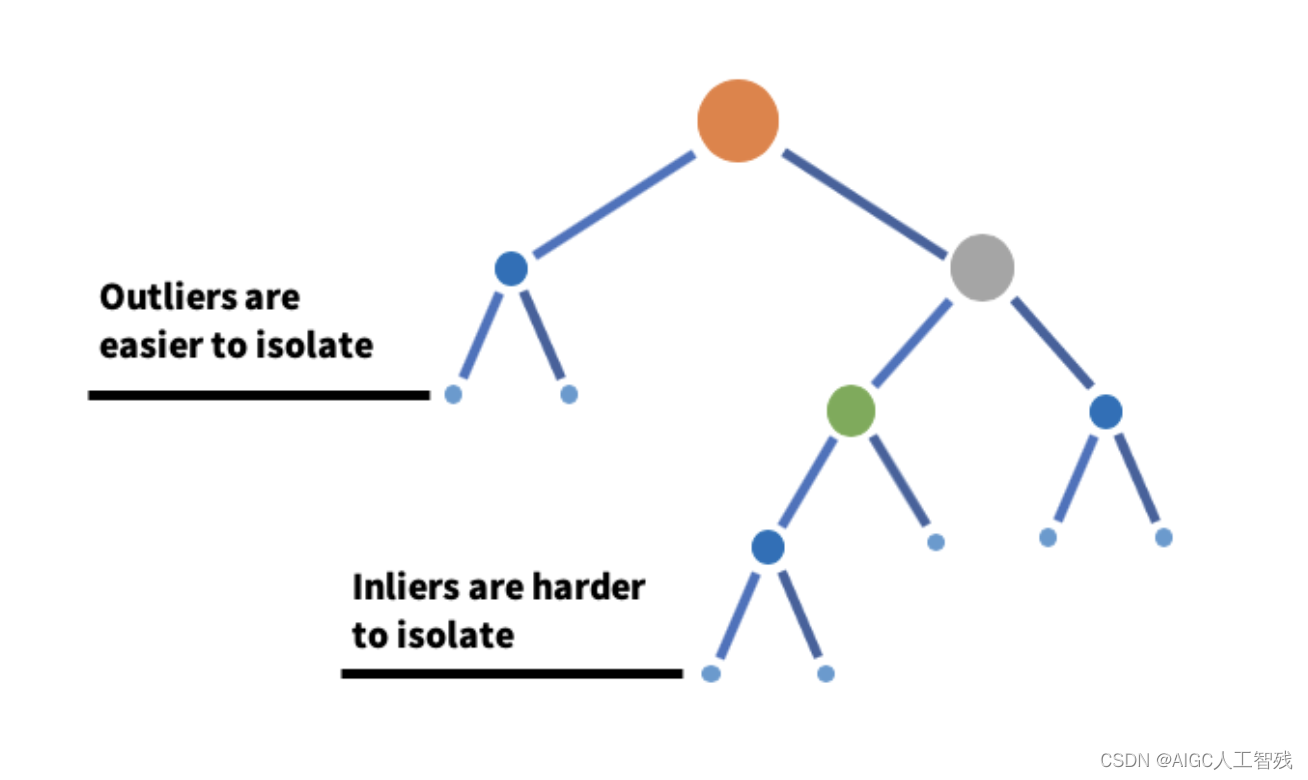
Isolation Forest(IF算法)

IF是采用二叉树的方法对数据进行切分，数据点在二叉树中的数据深度反应了该条数据的‘疏离’程度。整个过程也是训练跟预测两个步骤：

• 训练：抽取多个样本，构建多棵二叉树
• 预测：综合多棵二叉树的结果，计算每个数据点的异常值

我们以一维数据来进行简单理解IF算法的思想，我们有一个一维数据，想将A和B点切分出来：
（1）现在最大值和最小值之间随机选择一个x值，将大于x值和小于x值的数据分为两组；
（2）在两组数据中重复以上步骤，直到数据不可分，因为B点跟其他数据更远，所以只要比较少次数就能分离
（3）A点由于跟其他数据比较近，所以需要更多的次数才能切分出来。

我们不必了解它的公式，我们直到它最后的分值即可：

• 如果数据x在多个二叉树的平均路径长度都比较短，得分比较接近1，则数据x越异常；
• 如果数据x在多个二叉树的平均路径长度都比较长，则得分更接近0，则数据x越正常；
• 如果数据x在多个二叉树的平均路径长度是平均值，则得分为0.5。

IF例子

同LOF使用一样的数据

from pyod.models.iforest import IForest

data = pd.read_csv('Bcard.txt')
feature_lst = ['person_info','finance_info','credit_info','act_info']
# 划分数据
train = data[data.obs_mth != '2018-11-30'].reset_index().copy()
val = data[data.obs_mth == '2018-11-30'].reset_index().copy()
x = train[feature_lst]
y = train['bad_ind']

if_clf = IForest(behaviour='new', n_estimators=500, n_jobs=-1)
if_clf.fit(x)
out_pred = if_clf.predict_proba(x,method='linear')[:,1]
train['out_pred'] = out_pred

if_x = train[train.out_pred<0.7][feature_lst]
if_y = train[train.out_pred<0.7]['bad_ind']
val_x = val[feature_lst]
val_y = val['bad_ind']

# 训练模型
lr_model = LogisticRegression(C=0.1,class_weight='balanced')
lr_model.fit(if_x,if_y)

# 训练集
print('参数调整前的ks值')
y_pred = lr_model.predict_proba(if_x)[:,1] #取出训练集预测值
fpr_lr_train,tpr_lr_train,_ = roc_curve(if_y,y_pred) #计算TPR和FPR
train_ks = abs(fpr_lr_train - tpr_lr_train).max() #计算训练集KS
print('train_ks : ',train_ks)

#验证集
y_pred = lr_model.predict_proba(val_x)[:,1] #计算验证集预测值
fpr_lr,tpr_lr,_ = roc_curve(val_y,y_pred) #计算验证集预测值
val_ks = abs(fpr_lr - tpr_lr).max() #计算验证集KS值
print('val_ks : ',val_ks)

from matplotlib import pyplot as plt
plt.plot(fpr_lr_train,tpr_lr_train,label = 'train LR')
plt.plot(fpr_lr,tpr_lr,label = 'evl LR')
plt.plot([0,1],[0,1],'k--')
plt.xlabel('False positive rate')
plt.ylabel('True positive rate')
plt.title('ROC Curve')
plt.legend(loc = 'best')
plt.show()

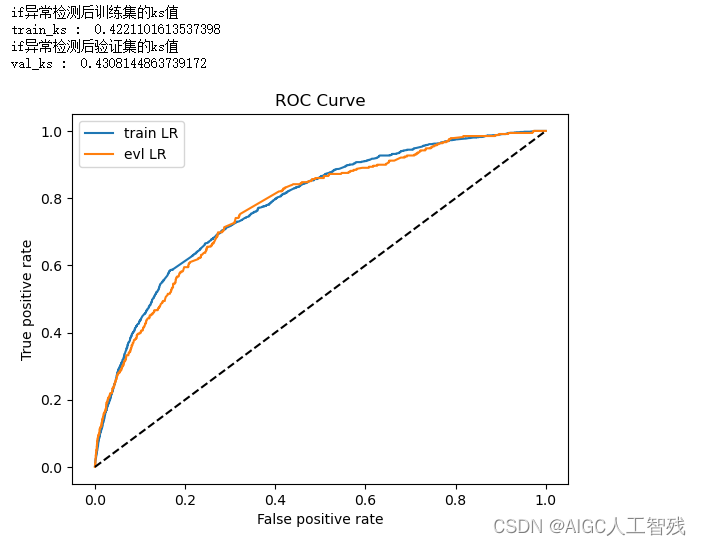
验证集的KS值有一定的上升。
原数据的ks值如下：