1143.最长公共子序列(注意递推的逻辑)

• 体会一下本题和 718. 最长重复子数组 的区别，主要是本题不连续，不连续的递推逻辑一定要注意

给定两个字符串 text1 和 text2，返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ，返回 0 。

一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。

• 例如，"ace" 是 "abcde" 的子序列，但 "aec" 不是 "abcde" 的子序列。

两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。

示例 1：

输入：text1 = "abcde", text2 = "ace" 
输出：3  
解释：最长公共子序列是 "ace" ，它的长度为 3 。

示例 2：

输入：text1 = "abc", text2 = "abc"
输出：3
解释：最长公共子序列是 "abc" ，它的长度为 3 。

示例 3：

输入：text1 = "abc", text2 = "def"
输出：0
解释：两个字符串没有公共子序列，返回 0 。

提示：

• 1 <= text1.length, text2.length <= 1000
• text1 和 text2 仅由小写英文字符组成。

思路

本题与 718.最长重复子数组 的区别就在于，本题不要求两个数组的重复元素连续了，但是需要保持元素的相对顺序。

如果不需要保持元素连续，那么一个重要区别就是，字符串包含的数字越多，两个数组的重复元素存在的可能性越高，包含数字多的字符串重复元素数量一定>=包含数字少的

DP数组含义

这类需要两个序列挨个对比的题目，DP数组含义最好都设置为：长度为[0,i-1]的字符串1和长度为[0,j-1]的字符串2，两个字符串的公共子序列长度为dp[i][j]，注意并不是最长，因为最长是单独用result变量去筛选的。

这样定义是为了后面代码实现方便，其实就是简化了dp数组第一行和第一列的初始化逻辑。详见上一题的博客。

递推公式

本题的递推比较重要，因为要求不连续的重复子序列长度，如果当前下标对应的数字相等，那么递推公式和上一题相同；如果当前下标对应的数字不等，也就是存在错位的情况，例如下图所示的例子：

（注意为了方便理解这里dp[i][j]直接写成了对应nums[i]和nums[j]）

像上图这个例子，我们可以看到下标i=4和下标j=0的情况是重复的，这种错位较大的重复情况，也可以通过对dp[i-1][j]和dp[i][j-1]进行传递得到！

也就是说，如果当前遍历到的下标不相等的话，可以通过传递dp[i-1][j]和dp[i][j-1]，获取之前错位的部分，相等元素的累积值！

完整的递推公式：

int result=0;
for(int i=1;i<=nums.size();i++){
    for(int j=1;j<=nums.size();j++){
        if(nums[i-1]==nums[j-1]){
            //如果相等长度++
            dp[i][j]=dp[i-1][j-1]+1;
        }
        else{//如果不相等，直接调取两个错位的累积值
            dp[i][j]=max(dp[i-1][j],dp[i],[j-1]);
        }
        result=max(result,dp[i][j]);
    }
}

初始化

因为本题DP数组的含义依旧是**dp[i][j]代表以下标nums[i-1]数字和下标nums[j-1]数字结尾的字符串最大公共序列长度**，因此初始化全部为0即可，dp[0][j]和dp[i][0]都是0。

完整版

class Solution {
public:
    int longestCommonSubsequence(string text1, string text2) {
        //全部初始化为0
        vector<vector<int>>dp(text1.size()+1,vector<int>(text2.size()+1,0));
        int result=0;
        for(int i=1;i<=text1.size();i++){
            for(int j=1;j<=text2.size();j++){
                if(text1[i-1]==text2[j-1]){//如果相等就前面基础上累积+1
                    dp[i][j]=dp[i-1][j-1]+1;
                }
                else{//如果不等就找两个错位的最大值
                    dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
                }
                result=max(result,dp[i][j]);//存放遍历过程中的最大值
            }
        }
        return result;
    }
};

• 时间复杂度: O(n * m)，其中 n 和 m 分别为 text1 和 text2 的长度
• 空间复杂度: O(n * m)

重要：该解法是否保持了元素顺序

例如：nums1=[1,4,2]，nums2=[1,2,4]，这两个数组输入上面解法，输出都是2。

也就是说，dp[1][2]和dp[2][1]都=2（此处i/j为方便理解采用原数组下标），是保留了元素顺序的，重复序列是{1,2}或者{1,4}！

能够保持元素顺序的原因，是因为 text1[i-1]==text2[j-1] 的时候，两个元素相等，此刻会同时后移，与他们同时的上一个元素的情况进行累加！也就是两个指针都往前移动一位，然后，在之前最长公共子序列的长度基础上+1，表示新加入了一个公共元素。

这样的话，[1,2,4]和[1,4,2]这样的情况，当a[1]=b[2]的时候，会同时前移去累加a[0]和b[1]，并不会与后面的情况进行累加！因此能够保持元素原有的顺序。

总结

• 本题最重要的是，理解当两个序列找不连续的重复子序列时，如果遍历到的两个元素数值不等，那么只需要对dp[i-1][j]和dp[i][j-1]取最大值，之前错位的相等情况就会一层层转移到当前位置！
• i是nums1的数组下标，j是nums2的数组下标，dp[i][j]是在两个数组里面分别取值，一定要搞清楚这一点！

1035.不相交的线（注意思路）

• 本题重点是明白，只要找重复数字的时候，数字相对顺序不改变，那么链接相同数字的直线就不会相交！

在两条独立的水平线上按给定的顺序写下 nums1 和 nums2 中的整数。

现在，可以绘制一些连接两个数字 nums1[i] 和 nums2[j] 的直线，这些直线需要同时满足满足：

• nums1[i] == nums2[j]
• 且绘制的直线不与任何其他连线（非水平线）相交。

请注意，连线即使在端点也不能相交：每个数字只能属于一条连线。

以这种方法绘制线条，并返回可以绘制的最大连线数。

示例 1：

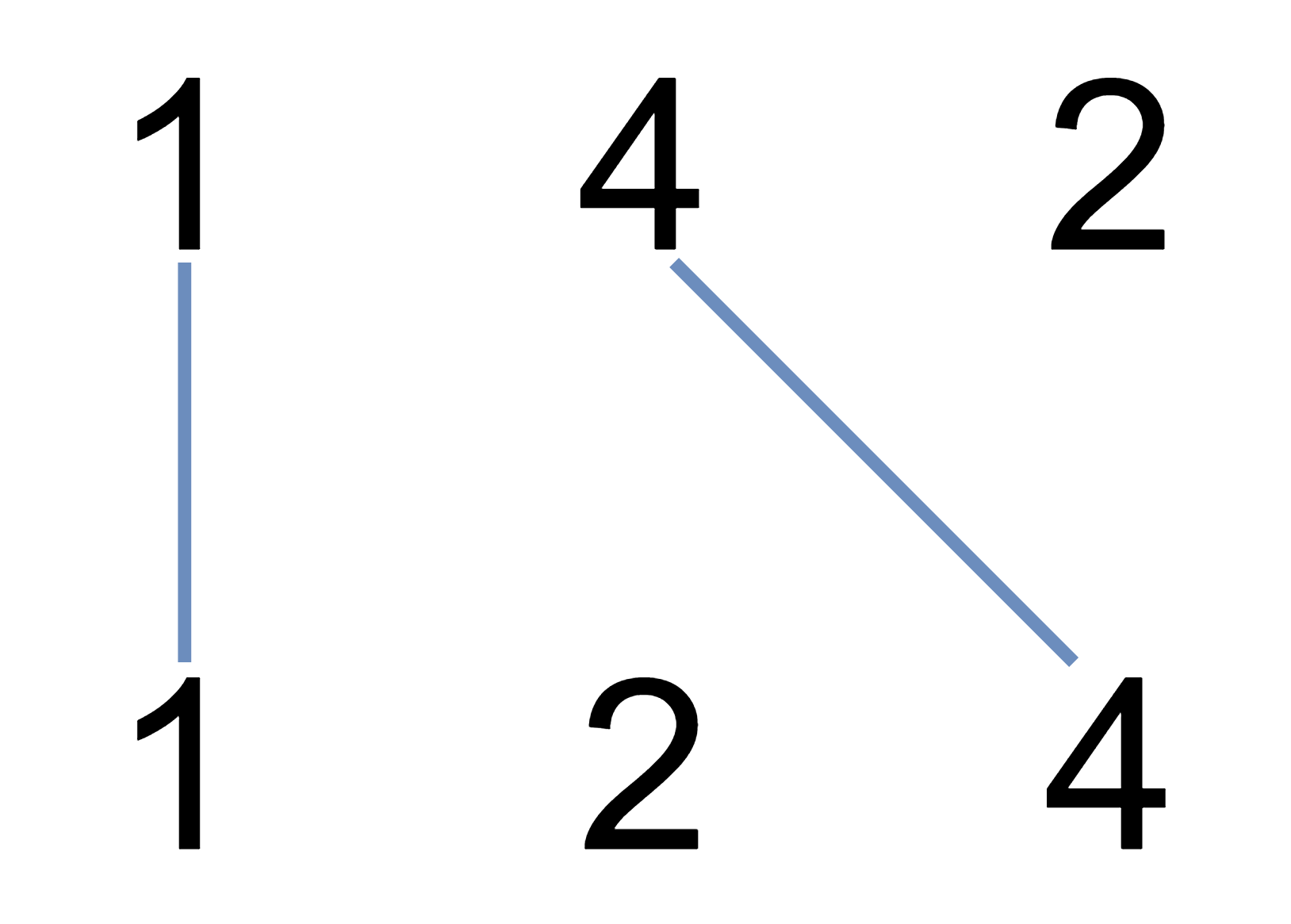
输入：nums1 = [1,4,2], nums2 = [1,2,4]
输出：2
解释：可以画出两条不交叉的线，如上图所示。 
但无法画出第三条不相交的直线，因为从 nums1[1]=4 到 nums2[2]=4 的直线将与从 nums1[2]=2 到 nums2[1]=2 的直线相交。

示例 2：

输入：nums1 = [2,5,1,2,5], nums2 = [10,5,2,1,5,2]
输出：3

示例 3：

输入：nums1 = [1,3,7,1,7,5], nums2 = [1,9,2,5,1]
输出：2

提示：

• 1 <= nums1.length, nums2.length <= 500
• 1 <= nums1[i], nums2[j] <= 2000

思路

本题一个核心点是连线必须不相交，实际上，连线不相交，意味着我们取两个序列相等数字的时候，需要保持元素原有的顺序。例如用例图中的情况：

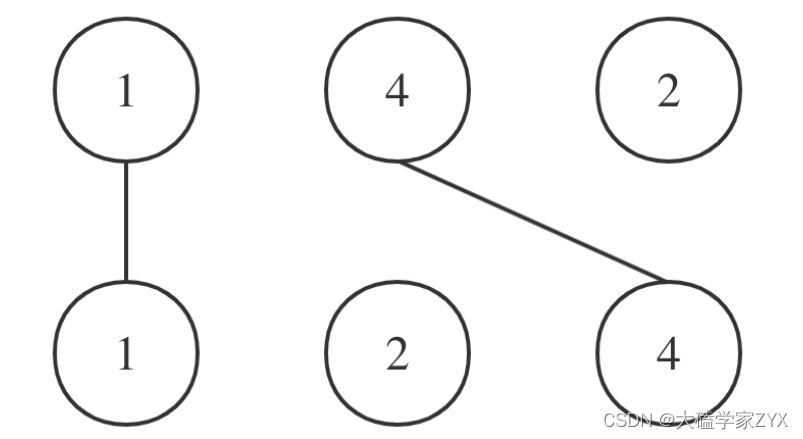
其实也就是说A和B的最长公共子序列是[1,4]，长度为2。 这个公共子序列指的是相对顺序不变（即数字4在字符串1中数字1的后面，那么数字4也应该在字符串2数字1的后面）。

只要找重复数字的时候，相对顺序不改变，那么链接相同数字的直线就不会相交！

明白了这一点之后，这道题实际上就和上一题：1143.最长公共子序列 一模一样了，只要找到不改变相对顺序的重复数字有多少个，就可以知道能连出来多少条线了。

完整版

class Solution {
public:
    int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {
        vector<vector<int>>dp(nums1.size()+1,vector<int>(nums2.size()+1,0));
        //初始化全部为0即可
        int result=0;
        for(int i=1;i<=nums1.size();i++){
            for(int j=1;j<=nums2.size();j++){
                if(nums[i-1]==nums[j-1]){
                    dp[i][j]=dp[i-1][j-1]+1;
                }
                else{
                    dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
                }
                result=max(result,dp[i][j]);
            }
        }
		return result;
    }
};

• 时间复杂度: O(n * m)
• 空间复杂度: O(n * m)

53.最大子序列和

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

子数组 是数组中的一个连续部分。

示例 1：

输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。

示例 2：

输入：nums = [1]
输出：1

示例 3：

输入：nums = [5,4,-1,7,8]
输出：23

提示：

• 1 <= nums.length <= 10^5
• -10^4 <= nums[i] <= 10^4

思路1：贪心

本题在贪心算法学习的时候整理过，因为这个题目数组里面有负数，负数累加只会让值变得更小。因此，与其使用-2这样的负数，不如重新开始，以新的位置作为连续和的起点。

局部最优：求解连续和为负数的时候，直接抛弃，以新的位置做起点

全局最优：得到最大的子数组连续和

贪心策略如下图所示。只要连续和是负数，负数一定没有正面作用，就立刻抛弃，选择下一个位置为起点。

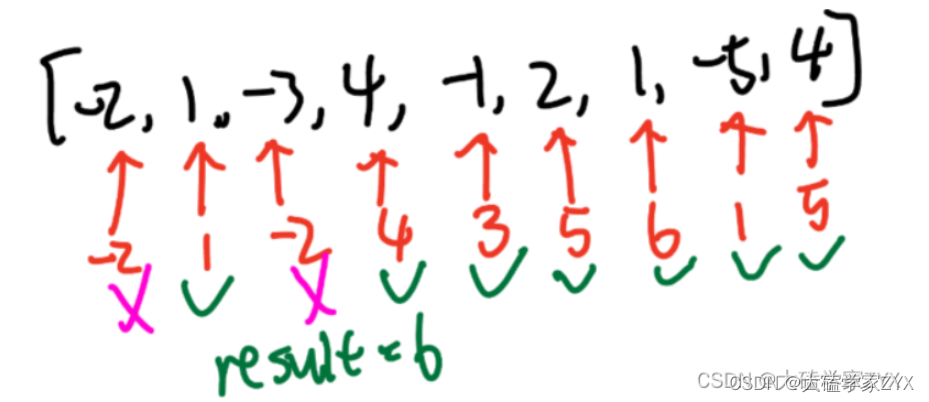
DAY36：贪心算法（三）最大子数组和+买卖股票最佳时机_大磕学家ZYX的博客-CSDN博客

思路1完整版

• 贪心的思路，核心在于找到局部最优，局部最优就是遇到了负数立刻放弃，从下一个数值开始重新求和

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int result=INT_MIN;
        int sum=0;
        for(int i=0;i<nums.size();i++){ 
            if(sum<0){
                sum=0;//直接重新置零
            }
            sum+=nums[i];
            result=max(result,sum);//记录sum的最大值
        }
        return result;
    }
};

思路2：动态规划

DP数组含义

本题dp[i]的含义是，以下标i（nums[i]）为结尾的最大连续子数组和是dp[i]

递推公式

因为dp[i]含义是以nums[i]为结尾的最长连续子序列和，那么，连续子数组必须以nums[i]结尾的话，只有之前的元素加上nums[i]和以nums[i]为开头重新计算数组和两种情况！

也就是说dp[i]只能从两个方向推出来，dp[i-1]+nums[i]和nums[i]。二者取最大值即可。

• 注意，因为本题要求连续数组，所以递推必须包含nums[i]在内！如果不包含i的话，下一个DP就一定不连续。

dp[i]=max(dp[i-1]+nums[i],nums[i]);

初始化

dp[0]表示以nums[0]为结尾的字符串最大和，也就是nums[0]本身。

dp[0]=nums[0];

完整版

lass Solution {
public:
    int maxSubArray(vector<int>& nums) {
        if(nums.size()==1) return nums[0];
        vector<int>dp(nums.size(),0);
        dp[0]=nums[0];
        int res=nums[0];//注意res的初始值
        for(int i=1;i<nums.size();i++){
            dp[i]=max(dp[i-1]+nums[i],nums[i]);
            res=max(res,dp[i]);
        }
        return res;
    }
};

• 时间复杂度：O(n)
• 空间复杂度：O(n)

总结

这道题目用贪心也很巧妙，动规的方法比较直接。

补充1：为什么不能用类似"打家劫舍"系列的"考虑下标i以内的数字"思想

DAY49：动态规划（十三）打家劫舍+打家劫舍Ⅱ+打家劫舍Ⅲ（树形DP）_大磕学家ZYX的博客-CSDN博客

本题如果利用”打家劫舍“系列的思想，也就是考虑下标i以内的房屋，但是不一定选择i，写出来的递推公式就会是这样：

• DP数组的定义是，考虑下标i以内的数字，其最大子数组和是dp[i]

dp[i]=max(dp[i-1]+nums[i],dp[i-1]);

但是这种做法是错误的，怎么改都改不出来，只有改成下面这种写法才能通过：

dp[i]=max(dp[i-1]+nums[i],nums[i]);

本质原因是因为这道题要求子数组连续，如果不选 i 的话，下一次 dp，就一定连不在一起了。

"打家劫舍"系列可以用考虑下标i以内的房子但是不一定偷i这种思想来表示DP数组，主要是因为题目要求不连续，不连续的情况，就可以仅仅是考虑下标i以内，而不是一定要选择下标i。

而本题因为要求的是连续的，不选i会不连续,所以必须加上i。

子序列类型题目，基本上定义的DP数组含义都是"以nums[i]为结尾的子字符串最大和"，都是**包含nums[i]**的情况，是因为这么写比较好做，方便状态转移。实际上这两种DP数组的定义方式很灵活，一种做不出来就换另一种。

补充2：为什么不能用滑动窗口

这道题其实并不适用于滑动窗口的方法，因为滑动窗口，通常适用于数组或列表中找到一个满足特定条件的连续子序列，例如和为特定值的子数组或具有特定数量的元素的子数组。

在这种情况下，我们通常在窗口大小或窗口中的元素总和等于特定值时调整窗口的大小。但在这个问题中，我们试图找到具有最大和的子序列，但我们并不知道这个子序列的长度。滑动的条件不够，只是限制了”最大和“，而没有限制和是多少。