🍉 吃瓜系列 教材:《机器学习》 周志华著
🕒时间:2023/7/26
目录
一、多元线性回归
1 向量化
1.1.1 向量化
1.1.2 使用最小二乘法构建损失函数
1.1.3 去除求和符号,改成向量点乘的形式
1.1.4 数学原理
2 求解 w(公式推导)
2.1.1 思路
2.1.2 证明损失函数的凸函数(国外)
2.1.3 矩阵微分公式知识:编辑
2.1.4 求一阶偏导数
2.1.5 求二阶偏导数
2.1.6 求 w
一、多元线性回归
多元线性回归是一种经典的统计分析方法,用于建立多个自变量(或解释变量)与一个因变量(或响应变量)之间的线性关系模型。
它是一种预测模型,可以通过对历史数据进行分析和建模,预测未来的结果。
- 多元线性回归的几何意义:
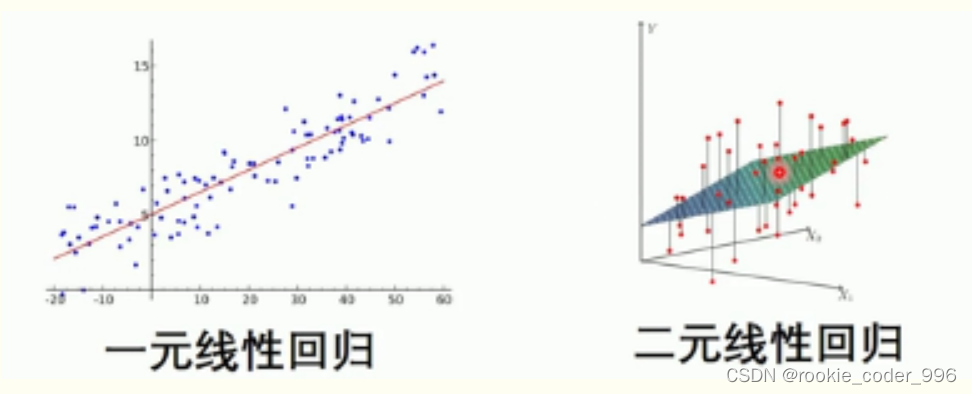
一元线性回归图形为一条直线
比一元线性回归更为复杂的是,多元线性回归组成的不是直线,是一个多维空间中的超平面,数据点散落在超平面的两侧。
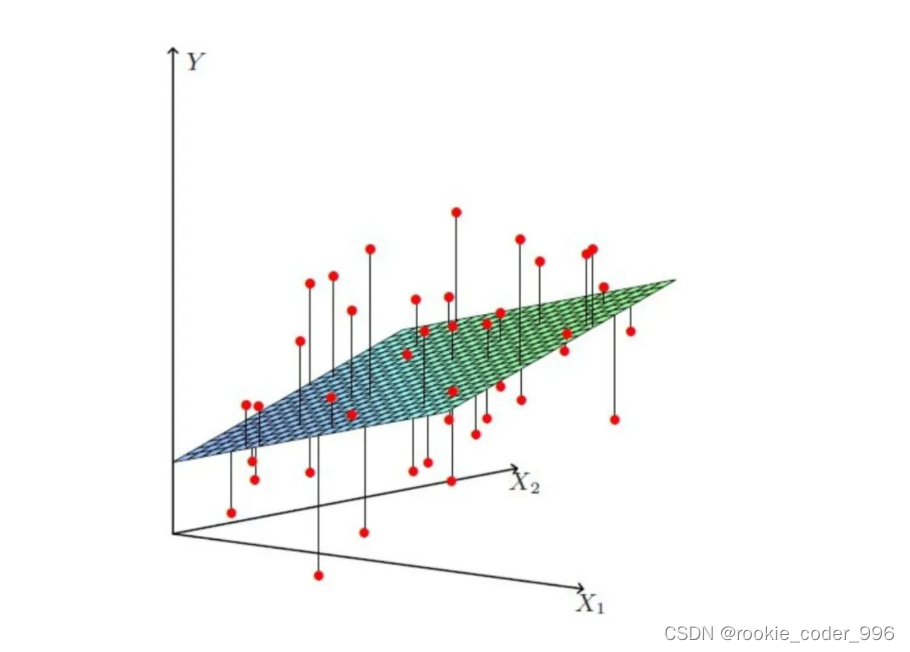
强调线性是因为大部分人用回归都是线性回归,线性的就是直线的,直线的就是简单的;什么是“回归”,回归就是向平均靠拢。
- 多元线性回归的应用
多元线性回归可以用于解决多个自变量与一个因变量之间的关系的问题,因为它可以考虑多个自变量对因变量的影响,从而更准确地预测因变量的值。以下是一些多元线性回归的应用:
- 1. 预测房价:房价可能与很多变量有关,如面积、地段、楼龄等等。多元线性回归可以结合这些因素来预测房价。
- 2. 产品销售预测:多元线性回归可以将多个市场因素考虑在内,如市场规模、市场份额、广告投入等等,来预测未来产品销售情况。
- 3. 股票价格预测:股票价格受到很多因素的影响,如经济环境、行业发展、公司业绩等等。多元线性回归可以将这些因素结合起来,预测股票价格的走势。
- 4. 贷款风险评估:为了评估贷款风险,银行可能需要考虑很多变量,如借款人的信用评级、贷款金额、收入情况等等。多元线性回归可以帮助银行根据这些因素来评估贷款的风险。
- 5. 医学研究:在医学研究中,多元线性回归可以用来研究不同因素对健康状况的影响,如疾病的发生率、治疗效果等等。
- 公式推导:
和一元线性回归的函数推广类似,从一元推广到多元
函数推广大多是类似的~
1 向量化
在多元线性回归中,我们试图找到一条最佳拟合曲线,使得自变量和因变量之间的误差最小化。
1.1.1 向量化
后面的参数 b 我们理解成 b = b ✖ 1
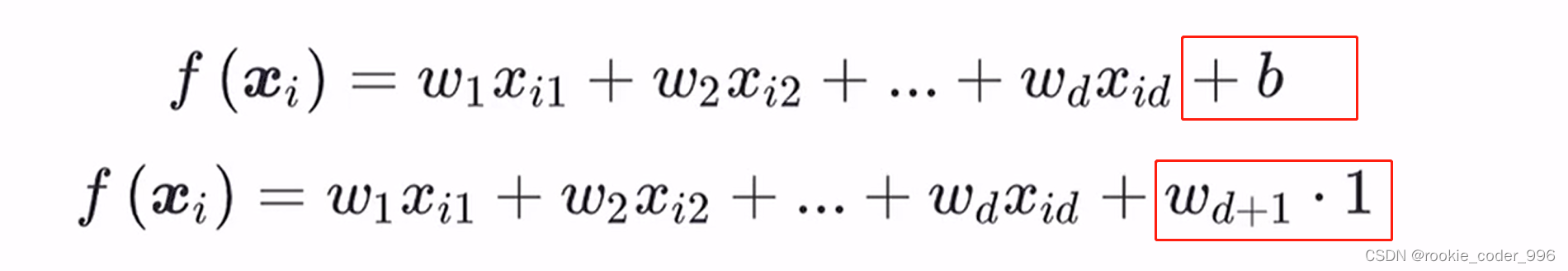

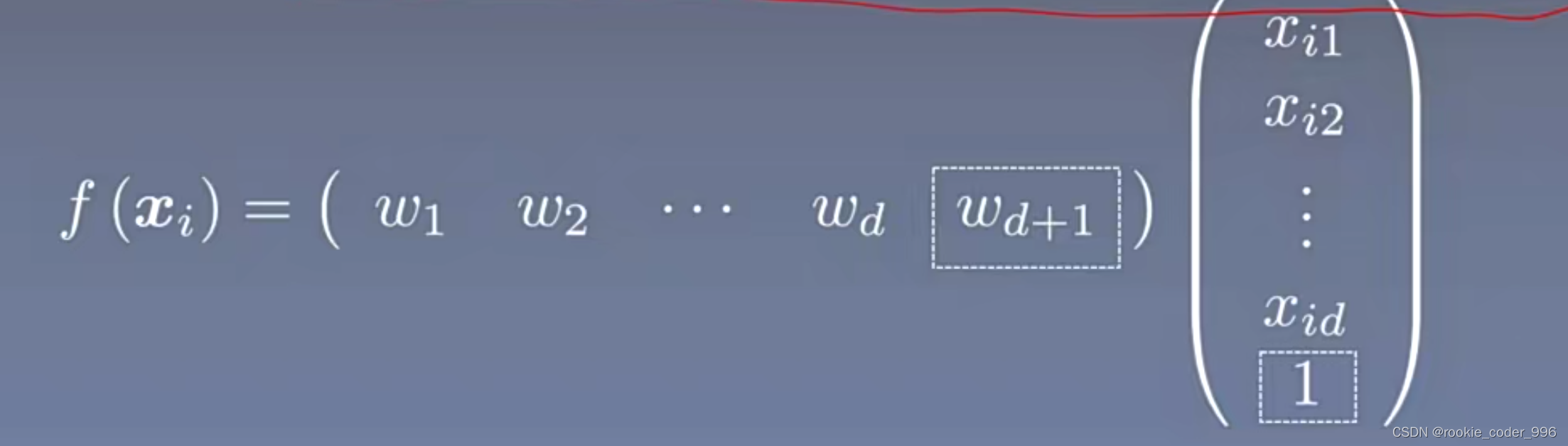
于是 我们构造处理一个权重向量 w 、 一个特征向量 x
使得:
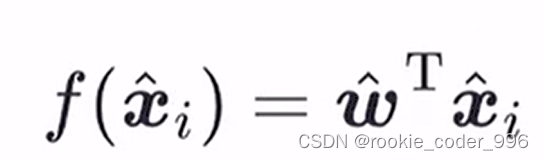
1.1.2 使用最小二乘法构建损失函数
多元线性回归通过最小二乘法求解模型系数,以建立自变量与因变量的线性关系模型,进而进行预测、分析和研究。
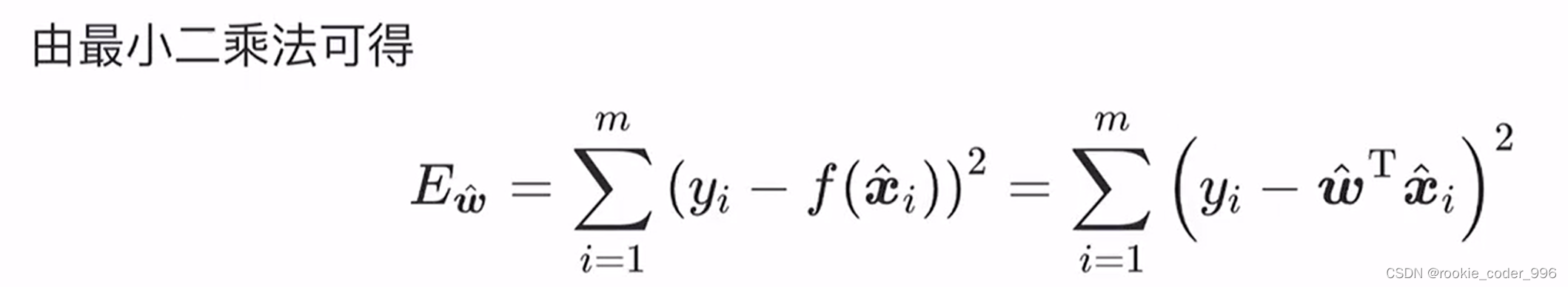
1.1.3 去除求和符号,改成向量点乘的形式
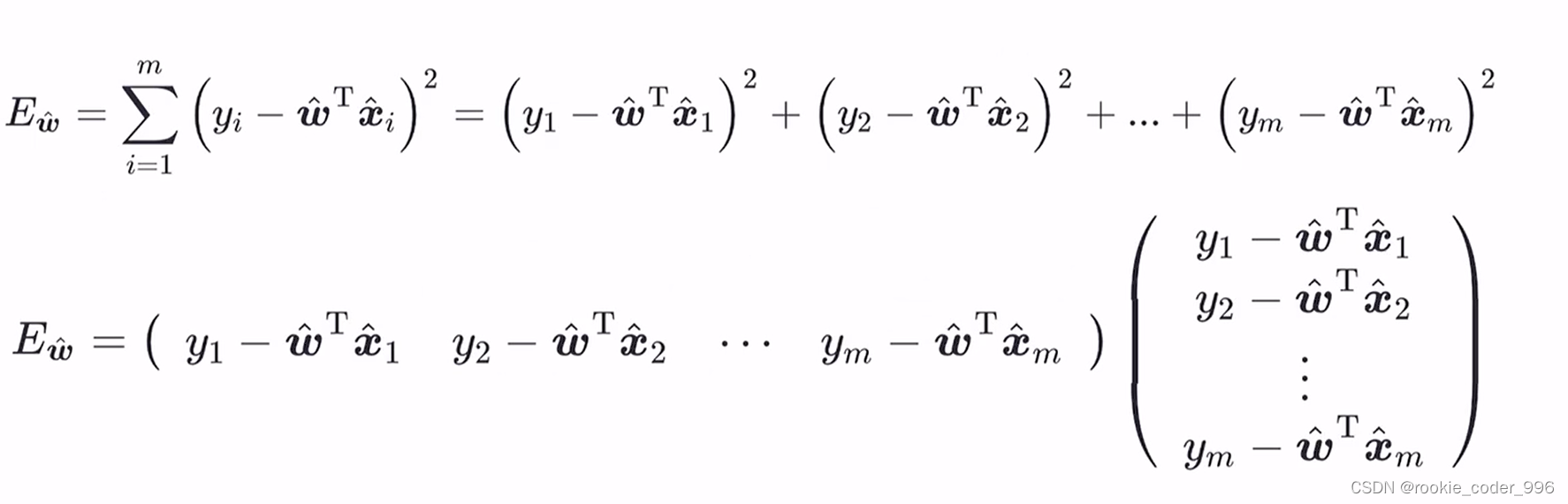
再次化简~
1.1.4 数学原理
这里的数学原理是 A转置×B = B 转置×A,都是一个数

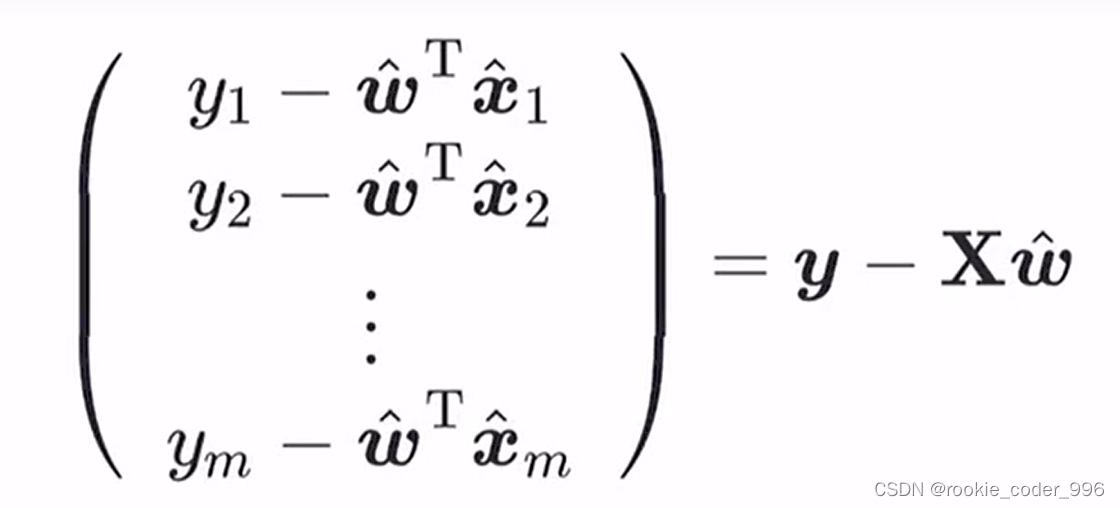
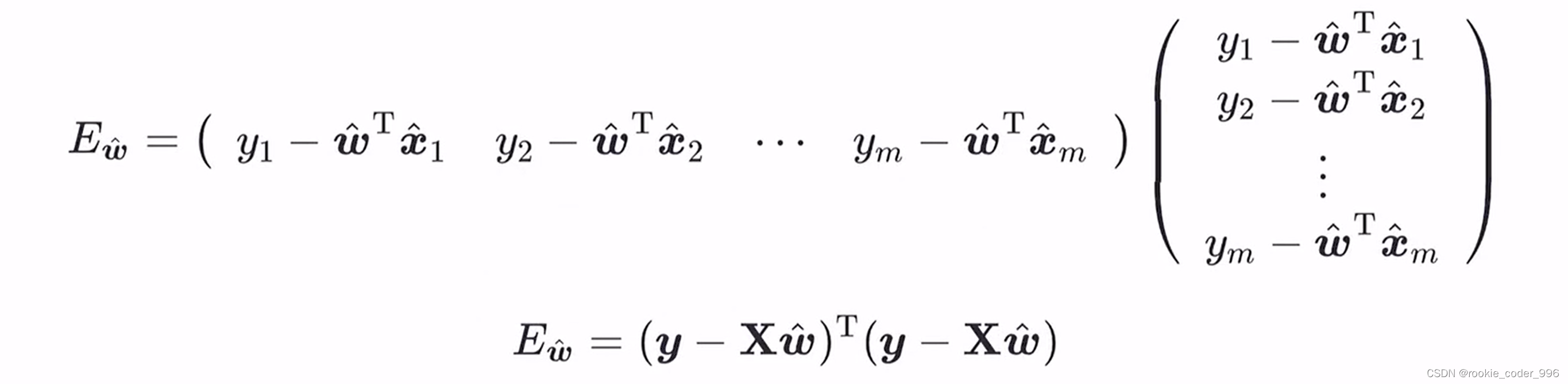
2 求解 w(公式推导)
2.1.1 思路
- 先证明,是凸函数(国外)
- 然后求解 w

2.1.2 证明损失函数的凸函数(国外)


2.1.3 矩阵微分公式知识:

2.1.4 求一阶偏导数
注意带入矩阵微分公式
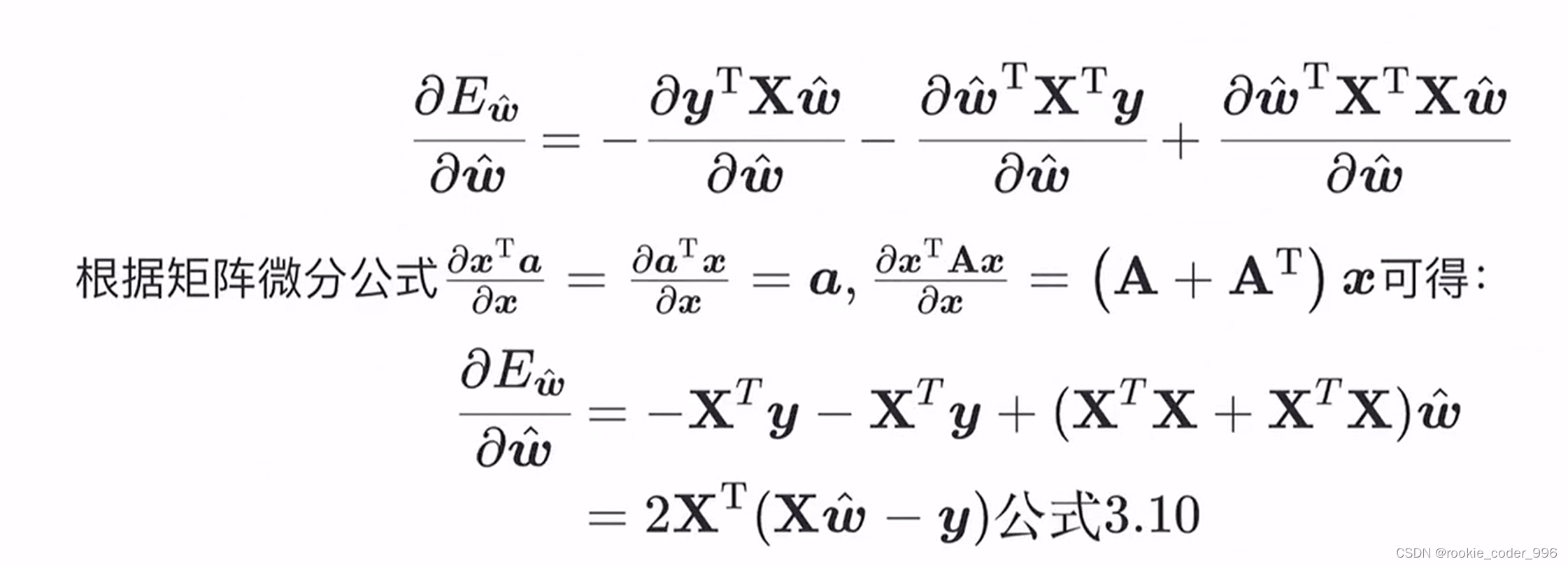
2.1.5 求二阶偏导数

值得注意的是 在此处的 X 的值不能保证 X^T X 一定是正定矩阵
西瓜书上是首先设定其是正定的!
先假定是正定矩阵! 才有后面的验证
证毕,该求解了
2.1.6 求 w

倒数第二行的依据是,首先等式两边同时除以2,然后在等式两边同时乘以逆 (X^TX)^-1