2023-07-28每日一题

一、题目编号

2050. 并行课程 III

二、题目链接

点击跳转到题目位置

三、题目描述

给你一个整数 n ，表示有 n 节课，课程编号从 1 到 n 。同时给你一个二维整数数组 relations ，其中 relations[j] = [prevCourse_j, nextCourse_j] ，表示课程 prevCoursej 必须在课程 nextCourse_j 之前完成（先修课的关系）。同时给你一个下标从 0 开始的整数数组 time ，其中 time[i] 表示完成第 (i+1) 门课程需要花费的月份数。

请你根据以下规则算出完成所有课程所需要的最少月份数：

如果一门课的所有先修课都已经完成，你可以在任意时间开始这门课程。
你可以同时上 任意门课程 。
请你返回完成所有课程所需要的最少月份数。

**注意：**测试数据保证一定可以完成所有课程（也就是先修课的关系构成一个有向无环图）。

提示：

1 <= n <= 5 * 104
0 <= relations.length <= min(n * (n - 1) / 2, 5 * 104)
relations[j].length == 2
1 <= prevCoursej, nextCoursej <= n
prevCoursej != nextCoursej
所有的先修课程对 [prevCoursej, nextCoursej] 都是 互不相同 的。
time.length == n
1 <= time[i] <= 104
先修课程图是一个有向无环图。

示例1：
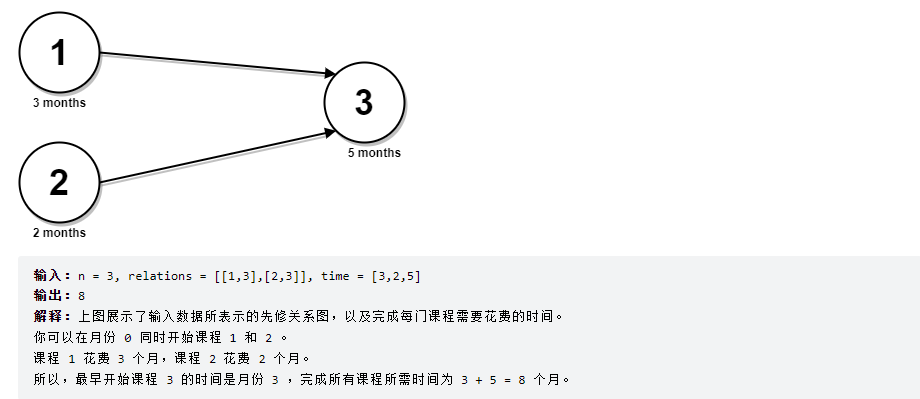
在这里插入图片描述

示例2：
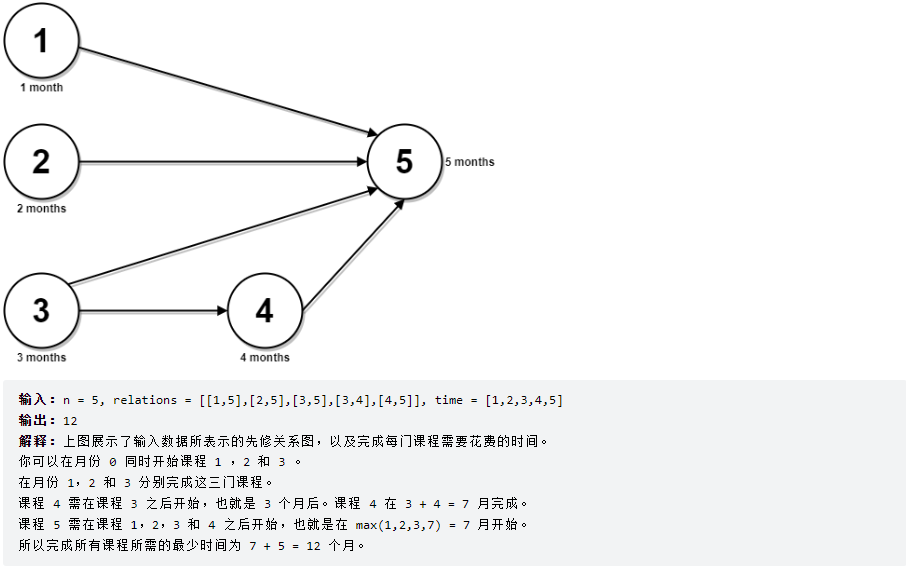
在这里插入图片描述

四、解题代码

class Solution {
public:
    int minimumTime(int n, vector<vector<int>>& relations, vector<int>& time) {
        int mx = 0;
        vector<vector<int>> prev(n + 1);
        for (auto &relation : relations) {
            int x = relation[0], y = relation[1];
            prev[y].emplace_back(x);
        }
        unordered_map<int, int> memo;
        function<int(int)> dp = [&](int i) -> int {
            if (!memo.count(i)) {
                int cur = 0;
                for (int p : prev[i]) {
                    cur = max(cur, dp(p));
                }
                cur += time[i - 1];
                memo[i] = cur;
            }
            return memo[i];
        };

        for (int i = 1; i <= n; i++) {
            mx = max(mx, dp(i));
        }
        return mx;
    }
};