【图像隐写】GBT+SVD数字水印嵌入与提取【含Matlab源码 1668期】

news2024/11/25 14:35:35

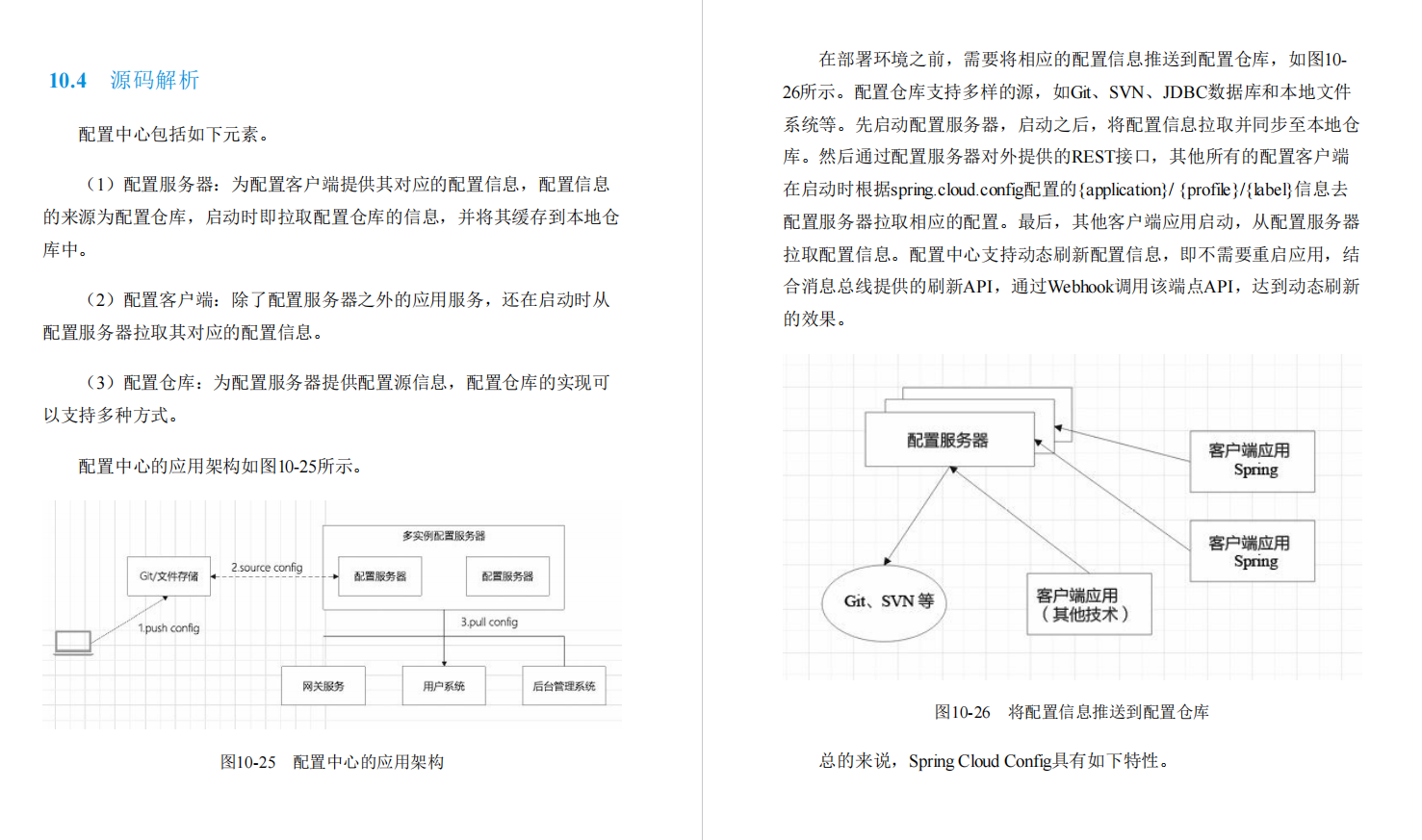
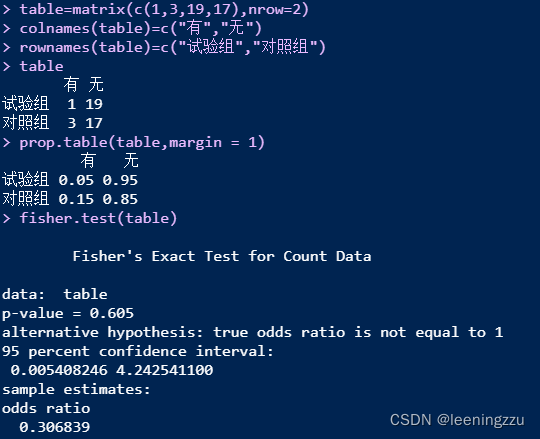
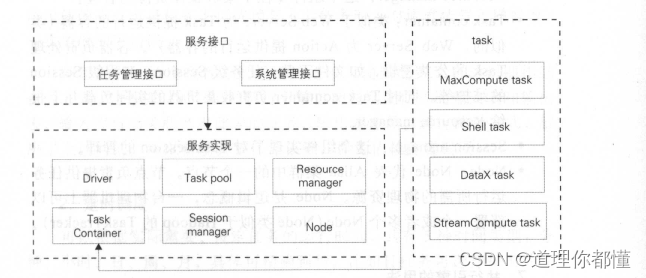
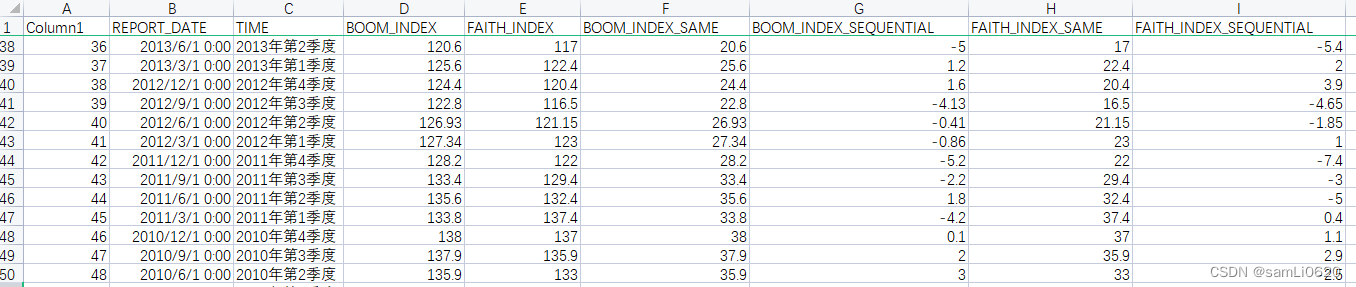
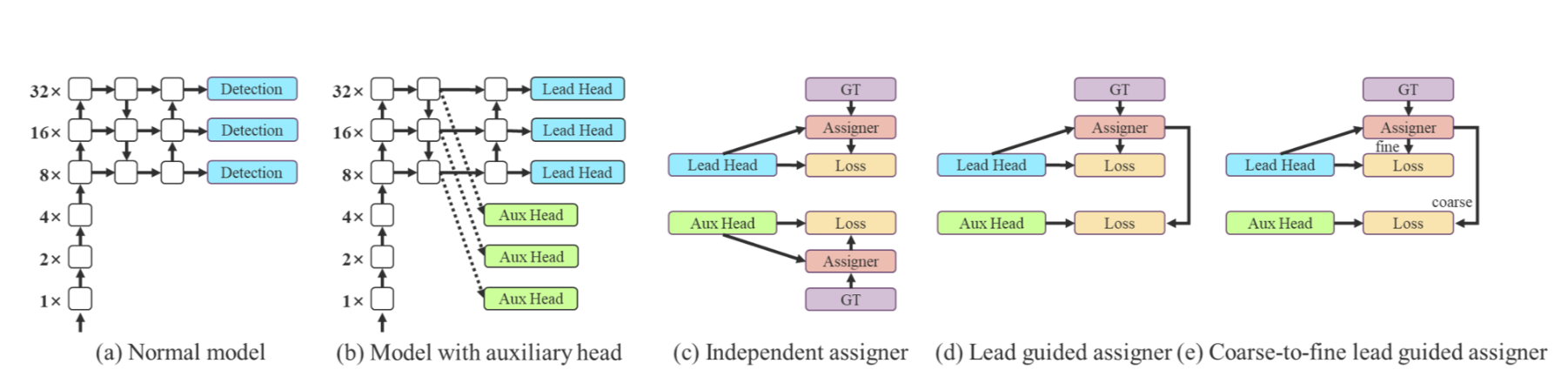
⛄一、SVD数字水印简介

理论知识参考文献：基于DWT和SVD的彩色图像数字水印算法研究
一种基于DWT-SVD的图像数字水印算法

⛄二、部分源代码

clc
close all
clear
%% Input images
I=imread(‘Lena.jpg’);
I=imresize(I,[512,512]);
logo=randsrc(8,8,[0,1]);

figure
subplot(1,4,1)
imshow(I)
title(‘原始图片’)
subplot(1,4,2)
B=I(:,:,3); % Blue Channel
imshow(logo)
xlabel(‘水印图片’)
gf=100; % Watermark Strength
n_gt=64; % <=64
zigzag=[1 9 2 3 10 17 25 18 11 4 5 12 19 26 33 41 34 27 20 13 6 7 14 21 28 35 42 49 57 …
50 43 36 29 22 15 8 16 23 30 37 44 51 58 59 52 45 38 31 24 32 39 46 53 60 61 54 47 40 48 55 62 63 56 64];
gt_idx=zigzag(1:n_gt);
%% key generation:
key=randperm(256256,6464);
%% Block Selection (Embedding Step):
c=0;
Watermarked_B=B;
for i=1:64:6464-63
c=c+1;
block_index=key(i:i+63);
blockB=double(reshape(B(block_index),[8,8]));
% graph-based transform:
gt_blockB=GT2(blockB);
% Singular Value Decomposition:
[U,S,V]=svd(gt_blockB(gt_idx));
sigmaB=S(1); % Biggest Singular Value
% embedding watermark image:
if logo©==1
S(1)=sigmaB+gf;
else
S(1)=sigmaB-gf;
end
reference{i}=S;
coeffs=USV; % inverse svd
rec_gt_block=zeros(8);
rec_gt_block(gt_idx)=coeffs;
rec_block=iGT2(rec_gt_block); % inverse gt
row_block=reshape(rec_block,1,64);
Watermarked_B(block_index)=row_block;
end
Watermarked_image=I;
Watermarked_image(:,:,3)=Watermarked_B;
subplot(1,4,3),
imshow(Watermarked_image);
title(‘嵌入水印的图片’)
%% Extraction Step
Ex_watermark=zeros(8);
Watermarked_B=Watermarked_image(:,:,3);
c=0;
for i=1:64:6464-63
c=c+1;
block_index=key(i:i+63);
blockB=double(reshape(B(block_index),[8,8]));
% graph transform:
gt_blockB=GT2(blockB);
% Singular Value Decomposition:
[Ub,Sb,Vb]=svd(gt_blockB(gt_idx));
Sbw=reference{i};
sigmaB=Sb(1); % Biggest Singular Value - Host
sigmaBW=Sbw(1); % Biggest Singular Value - Watermarked
% Extracting watermark image:
if sigmaBW>sigmaB
Ex_watermark©=1;
end
end
subplot(1,4,4),
imshow(Ex_watermark)
xlabel(‘提取水印’);
Bit_Error_Rate=sum(sum(Ex_watermark~=logo))/numel(logo)
Structure_Similarity_Index=ssim(Watermarked_image,I)
Peak_Signal_toNoise_Ratio=psnr(Watermarked_image,I)