2004年试题
Hermite矩阵酉相似于对角阵

验证相容矩阵范数

盖尔圆盘互不相交,则特征值都不相同,若盖尔圆盘全部出现在右半复平面上,则特征值全为实数。


矩阵二范数的计算

最大秩分解+M-P广义逆矩阵+方程是否有解

2005年试题
正定矩阵,对任意非零向量X,其正定二次型都大于0

矩阵二范数与特征值之间的转换

AA-为幂等矩阵,幂等矩阵特征值非零即一,A≠0,rank(A)=rank(AA-)≥1,所以AA-特征值必为1

初等酉变换对应的酉矩阵,酉矩阵的算子范数为1

矩阵的特征值小于等于任意相容的矩阵范数
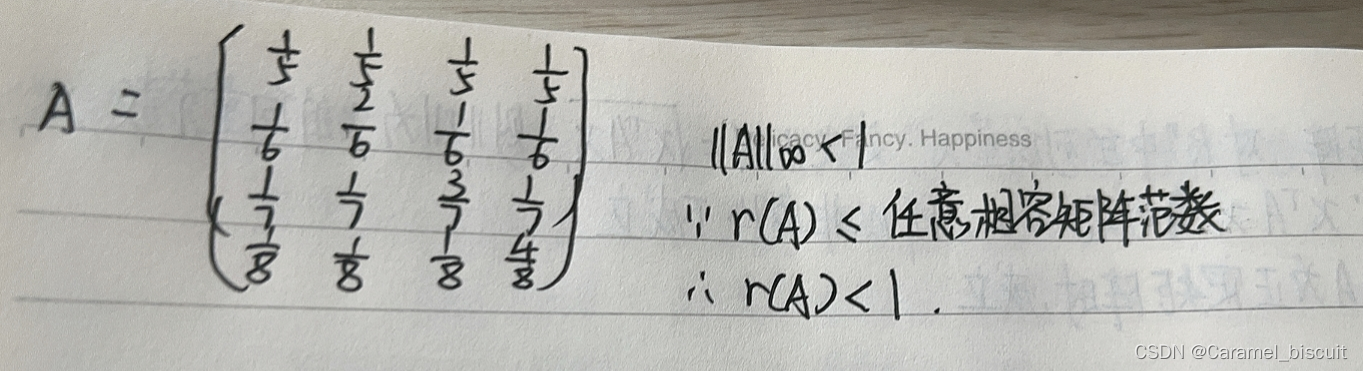
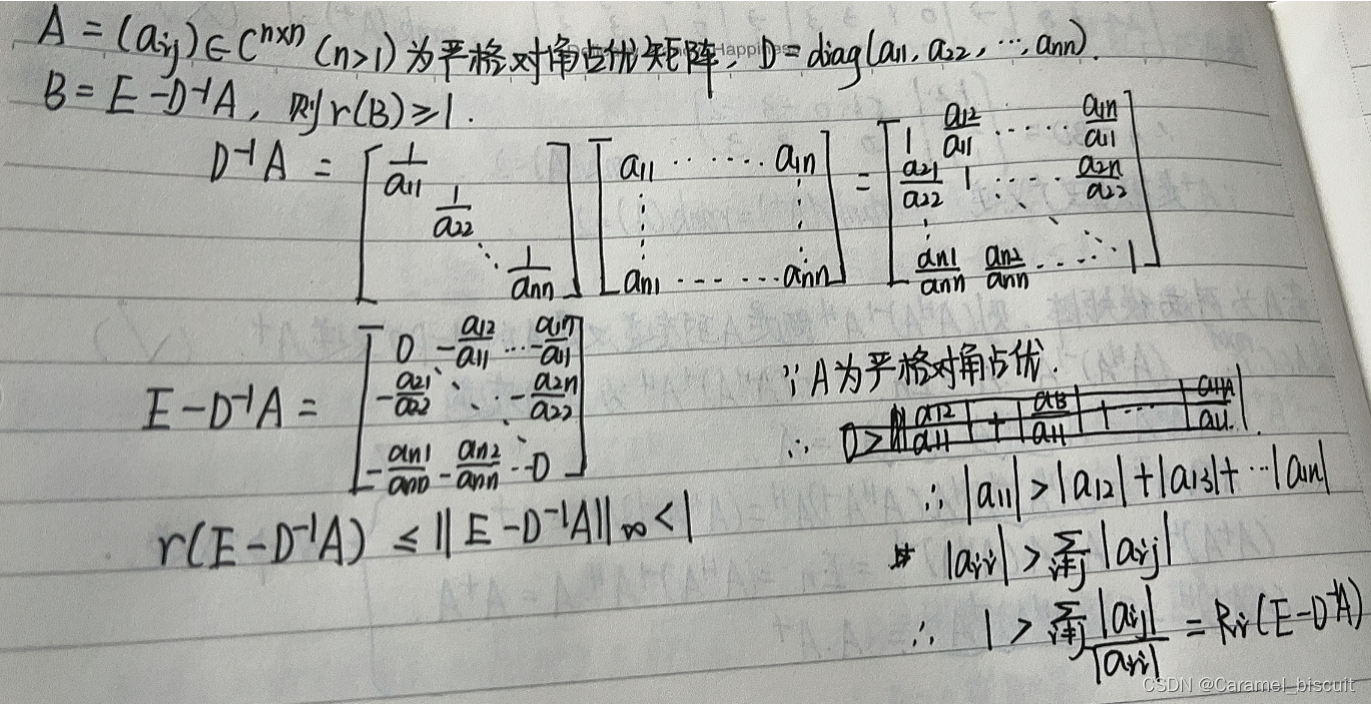
严格对角占优矩阵,A的最大特征值小于2A的矩阵无穷范数

向量范数的比较
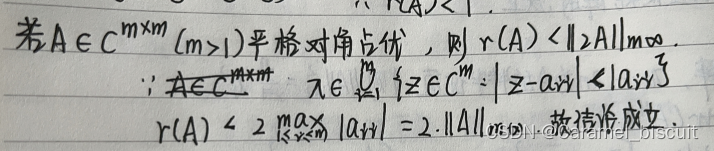
广义逆矩阵的性质,r阶单位矩阵的秩为r
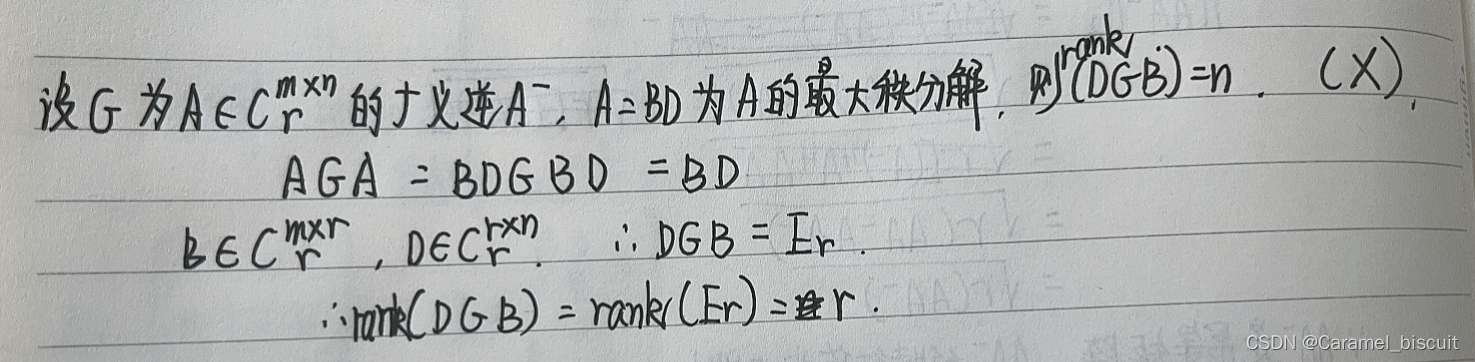
盖尔圆盘定理判定特征值的取值范围

证明矩阵范数与算子范数相容

正规矩阵属于不同特征值的特征向量彼此正交;正规矩阵对应的特征值和特征向量,其Hermite型矩阵对应该特征值的复数形式和相同的特征向量
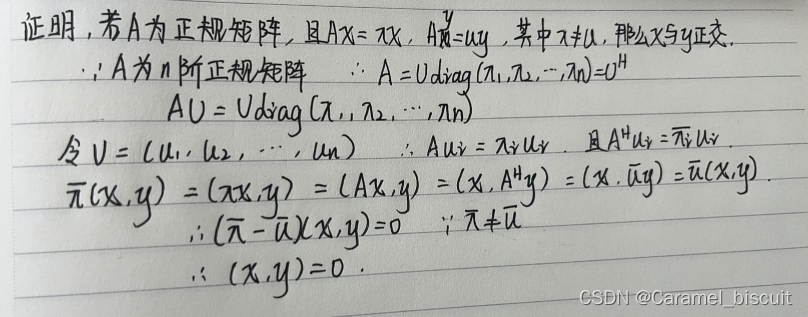
矩阵范数的证明

求矩阵的广义逆以及最佳逼近解

严格对角占优矩阵的性质:对角线元素的绝对值大于对应行/列其它元素绝对值之和
矩阵的最大特征值的绝对值(谱半径)小于等于相容的矩阵范数。
2006年试题
幂等矩阵特征值非零即一,当该矩阵不可逆时,特征值就只能为1

算子二范数与奇异值和特征值之间的转换

有逆凑单位矩阵
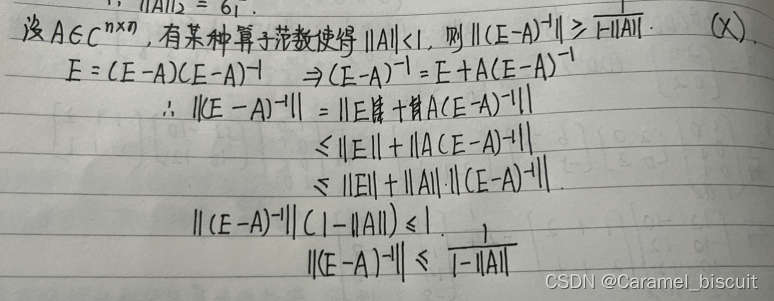
n阶酉矩阵的矩阵二范数等于根号n

A的秩=A的Hermite转置的秩=A的自反广义逆的秩;A的M-P广义逆矩阵也是A的自反广义逆矩阵

列满秩矩阵的左逆也是其M-P广义逆
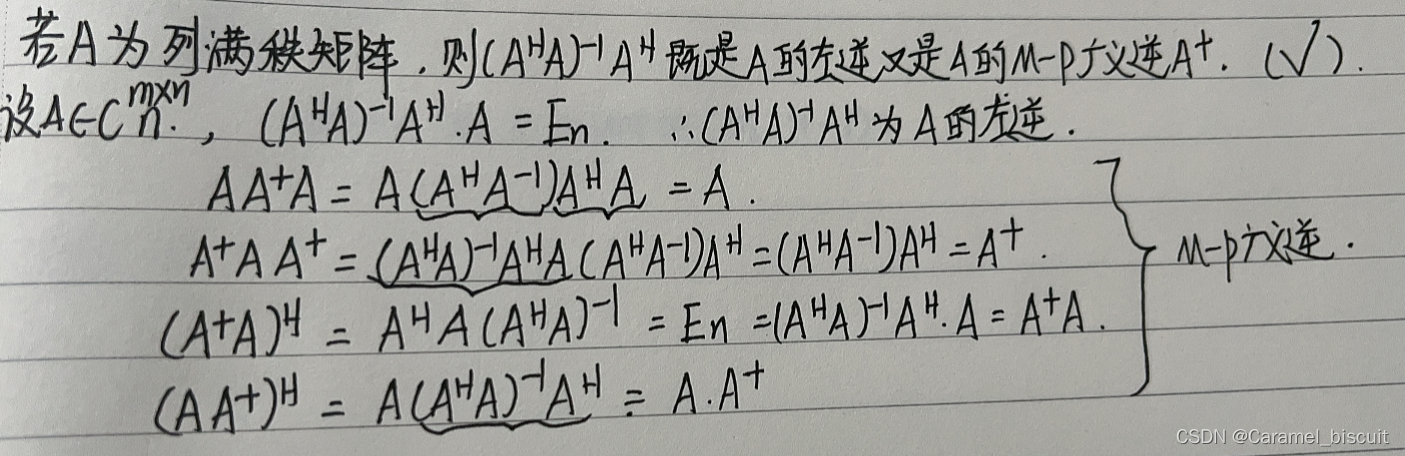
范数的判定
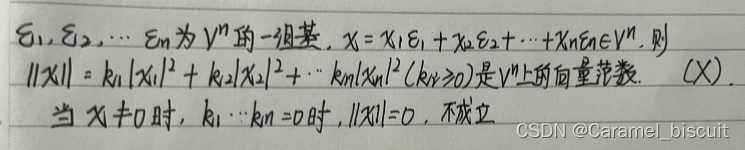
盖尔圆盘定理的应用

之前考试考过
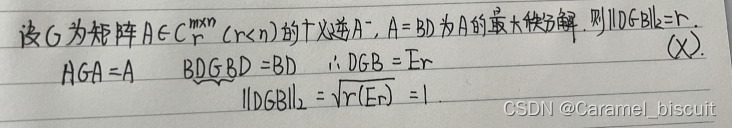









![[附源码]Python计算机毕业设计SSM基于的网上拍卖系统(程序+LW)](https://img-blog.csdnimg.cn/0ee59d788c454c79a3a2927a90e68a97.png)