文章目录
- 插入排序
- 直接插入排序
- 希尔排序
- 选择排序
- 选择排序
- 堆排序
- 交换排序
- 冒泡排序
- 快速排序
- hoare版
- 挖坑法
- 前后指针法
- 快速排序的递归展开图
- 快速排序的优化
- 三数取中法
- 快速排序的非递归实现
- 归并排序

插入排序
插入排序分为直接插入排序和希尔排序,其中希尔排序是很值得学习的算法
希尔排序的基础是直接插入排序,先学习直接插入排序
直接插入排序
直接插入排序类似于打扑克牌前的整牌的过程,假设我们现在有2 4 5 3四张牌,那么应该怎么整牌?
方法很简单,把3插到2和4中间,这样就完成了整牌的过程,而插入排序的算法就是这样的过程
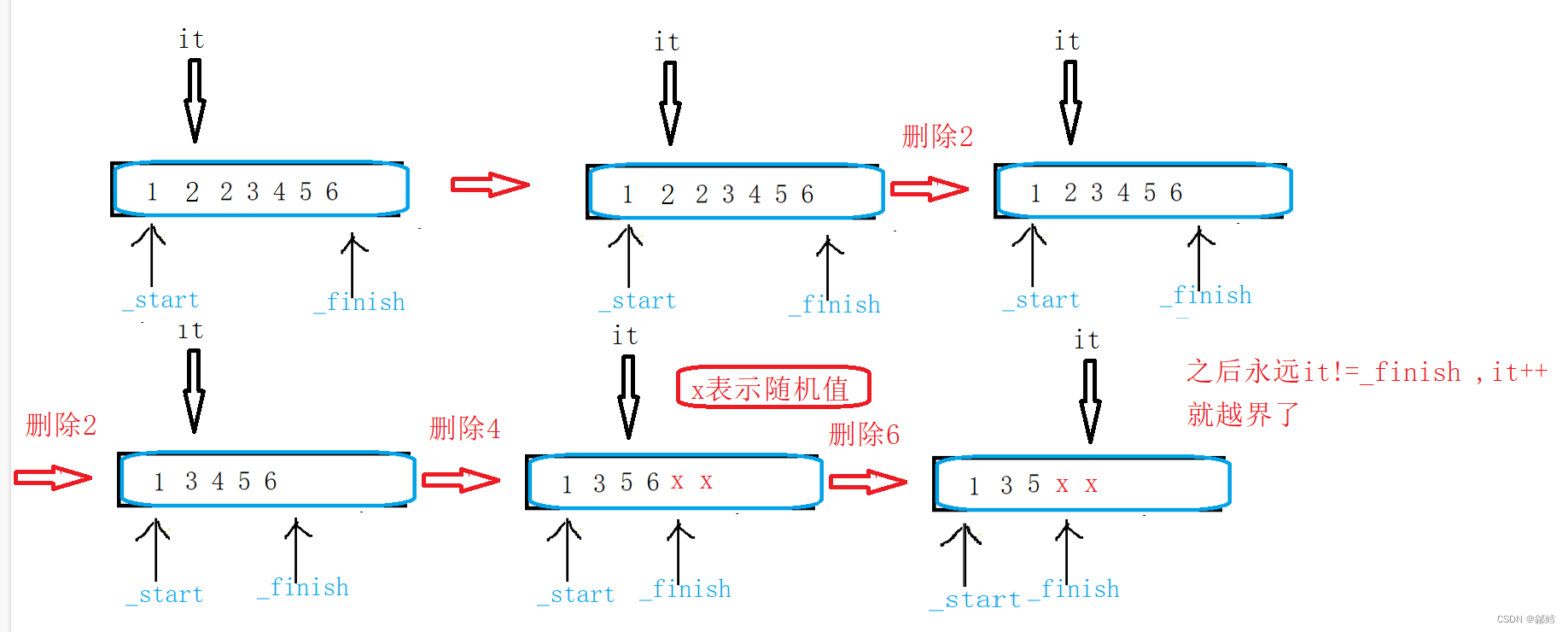
插入排序的基本原理图如下所示
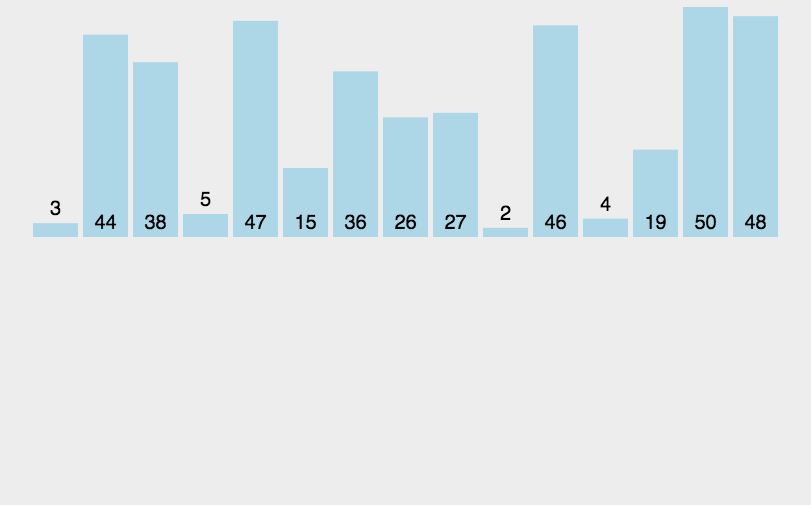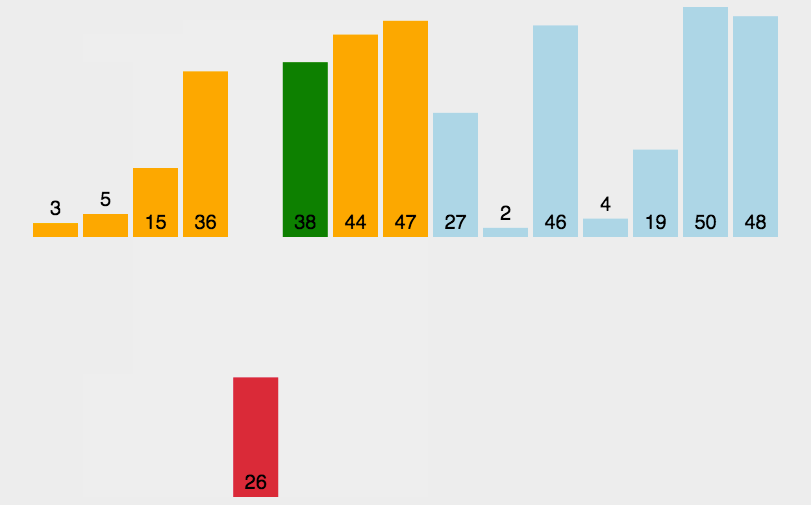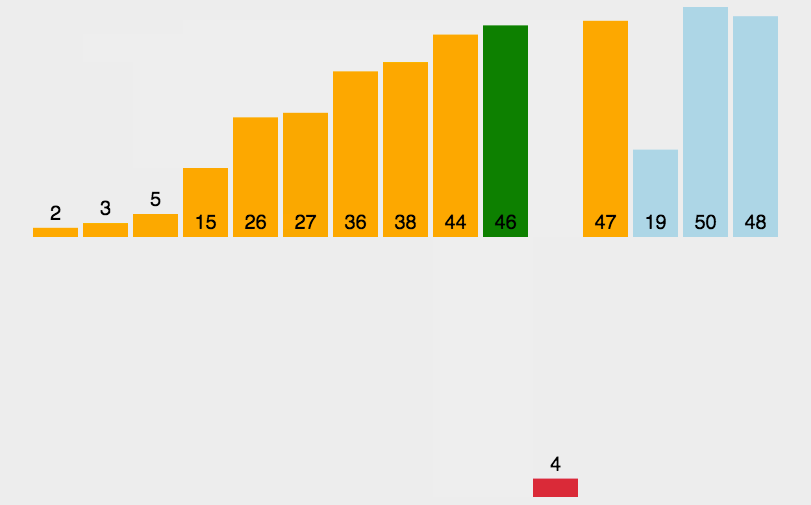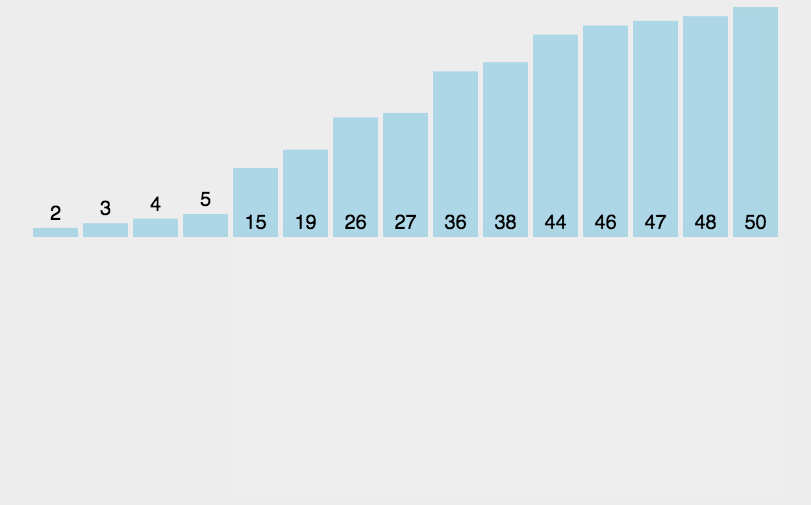
我们在这里定义end为已经排查结束的,排好序的一段数据的最后一个元素,tmp作为存储要移动的元素,那么具体实现方法如下:
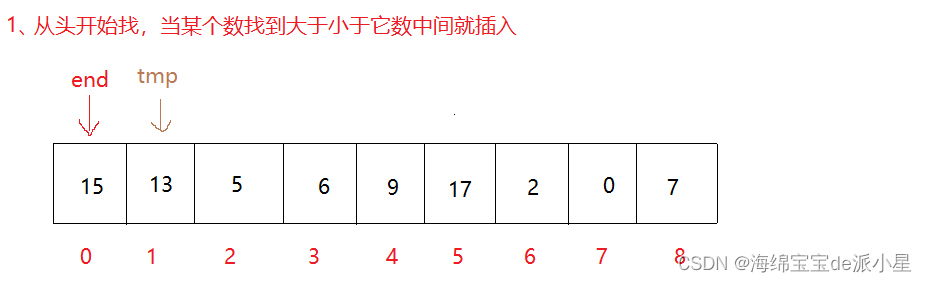
这里找到了tmp确实比end要小,于是下一步是要让tmp移动到end前面这段有序的数据中的合适的位置
算法实现的思想是:tmp如果比end的值小,那么就让end的值向后移动,end再指向前一个,再比较覆盖移动…直到tmp的值不比end小或者end直接走出数组,如果走出数组就让tmp成为新的首元素
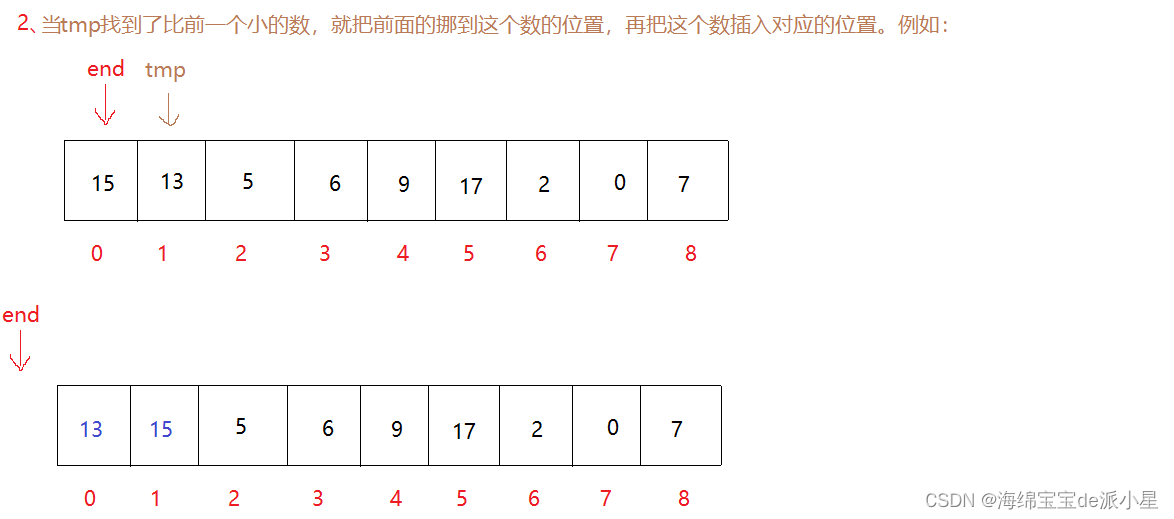
这样就完成了一次插入,那么接着进行一次排序:
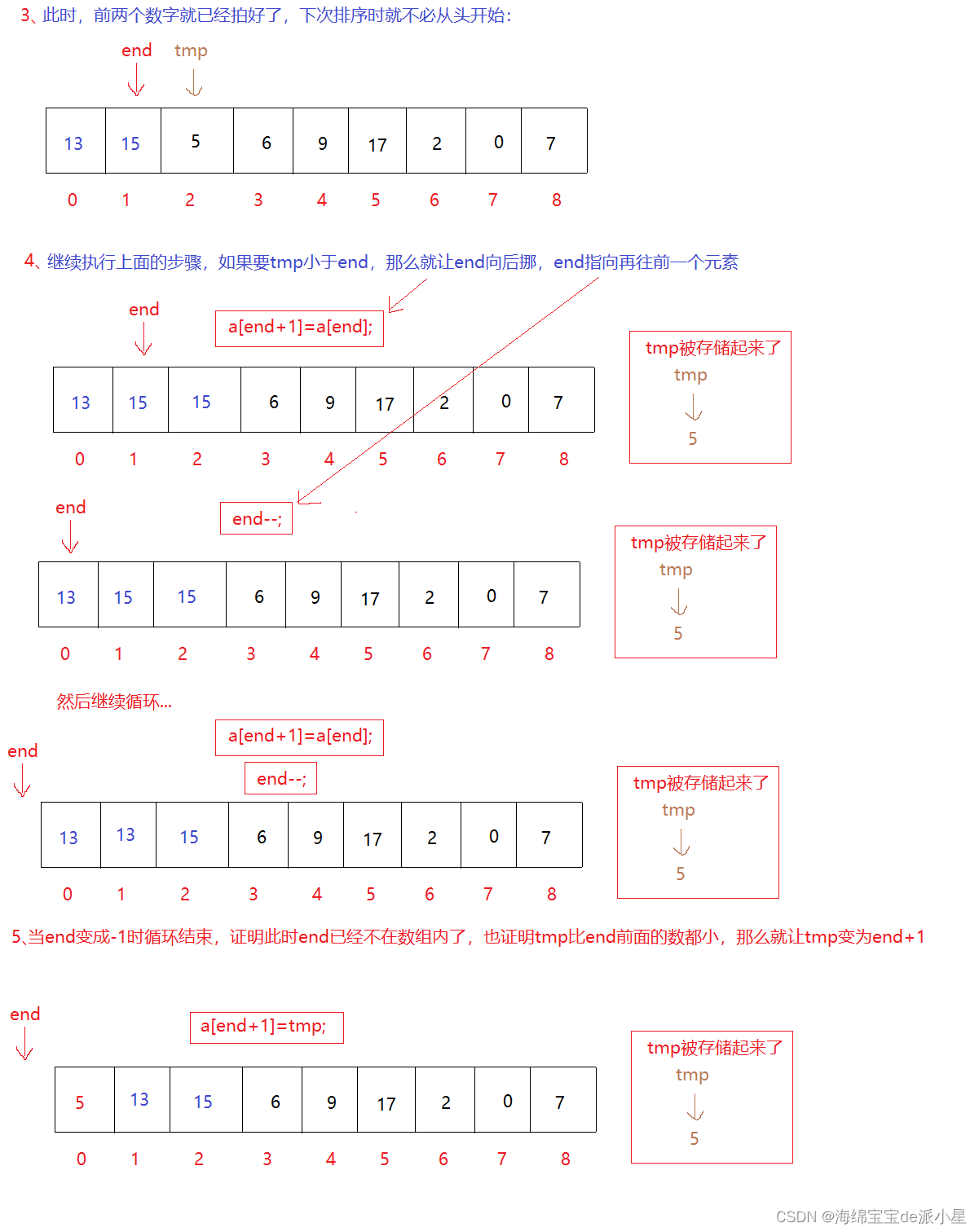
从中可以看出,插入排序整体的思想并不算复杂,代码实现相对也更简单,直接插入排序的价值在于给希尔排序做准备
插入排序的实现如下:
void InsertSort(int* a, int n)
{
for (int i = 0; i < n - 1; i++)
{
int end = i; // 找到有序数组的最后一个元素
int tmp = a[i + 1]; // 要参与插入排序的元素
while (end >= 0)
{
if (a[end] > tmp)
{
// 进行覆盖
a[end + 1] = a[end];
end--;
}
else
{
break;
}
}
a[end + 1] = tmp;
}
}
直接插入排序的时间复杂度也不难分析,是O(N^2),和冒泡排序在同一个水平,并不算高效
直接插入排序更多是给希尔排序做铺垫,希尔排序是很重要的排序,处理数据的效率可以和快速排序看齐
希尔排序
上面学完了插入排序,那么就必须总结一下插入排序的弊端
- 插入排序在对几乎已经排好序的数据操作时,效率高,即可以达到线性排序的效率。
- 但插入排序一般来说是低效的,因为插入排序每次只能将数据移动一位。
于是,希尔排序就是基于上面这两个问题进行解决的:
首先,插入排序对于已经排序差不多的序列有很强的效率,但与此同时它一次只能调整一个元素的位置,因此希尔就发明了希尔排序,它具体的操作几乎和插入排序相同,只是在插入排序的基础上,前面多了预排序的步骤,预排序是相当重要的,可以把一段数据的大小排序基本相同
那预排序的实现是如何实现的?
首先把数据进行分组,假设分成3组,下面的图片演示了这个过程

分好组后,对每一组元素单独进行插入排序
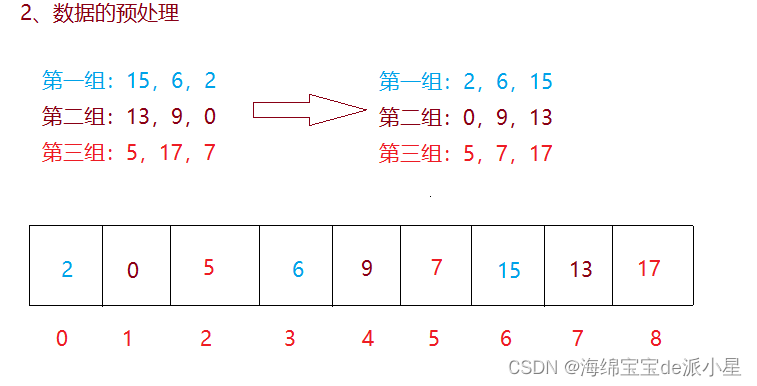
此时,序列里的数据就已经很接近有序了,再对这里的数据进行插入排序,可以完美适应插入排序的优点
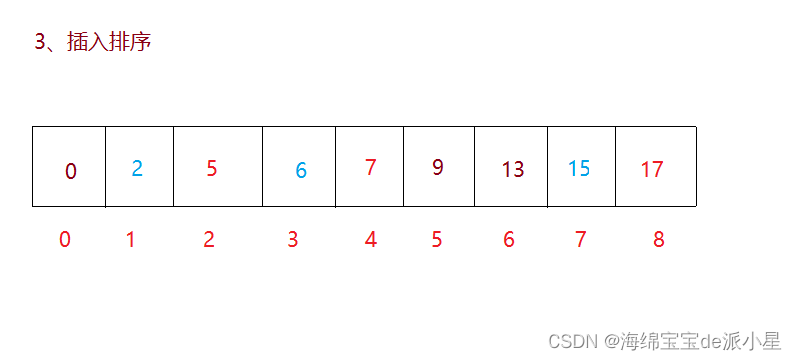
这里只是写了希尔排序的基本思想是如何工作的,具体的代码实现较为复杂
那么下一个问题就有了,为什么gap是3?如果数据量特别大还是3吗?gap的选择应该如何选择?
这里对gap要进行理解,gap到底是用来做什么的,它的大小会对最终结果造成什么影响
gap是对数据进行预处理阶段选择的大小,通过gap可以把数据变得相对有序一点,而gap越大,说明分的组越多,每一组的数据就越少,gap越小,分的就越细,就越接近真正的有序,当gap为1的时候,此时序列只有一组,那么就排成了真正的有序
代码实现如下:
void ShellSort(int* a, int n)
{
int gap = n;
while (gap > 1)
{
gap = gap / 3 + 1;
for (int i = 0; i < n - gap; i++)
{
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (a[end] > tmp)
{
a[end + gap] = a[end];
end = end - gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}
}
}
这里重点理解两点
gap = gap / 3 + 1; // 这句的目的是什么?
gap==1 // 是什么
gap=gap/3+1会让gap的最终结果一定为1
而gap为1的时候,此时就是插入排序,而序列也接近有序,插入排序的优点可以很好的被利用
希尔排序的时间复杂度相当难算,需要建立复杂的数学模型,这里直接说结论,希尔排序的时间复杂度大体上是接近于 O(N^1.3) 整体看效率是不低的,值得深入钻研学习
选择排序
选择排序
基础版的选择排序实现是很简单的,算法思路如下
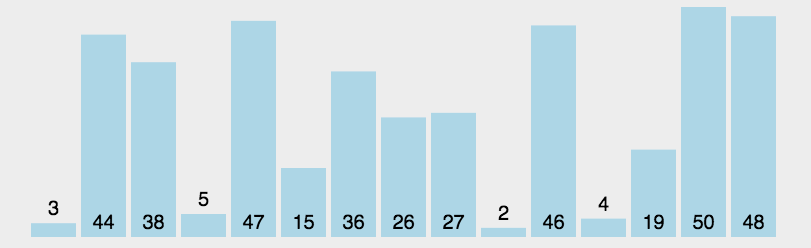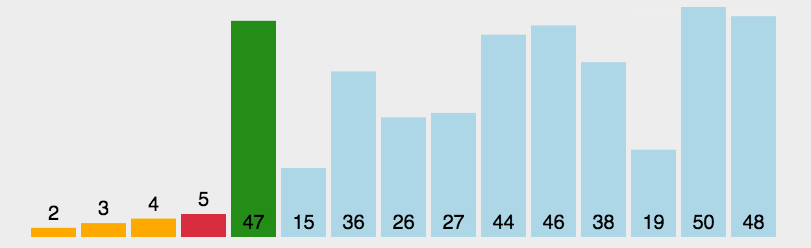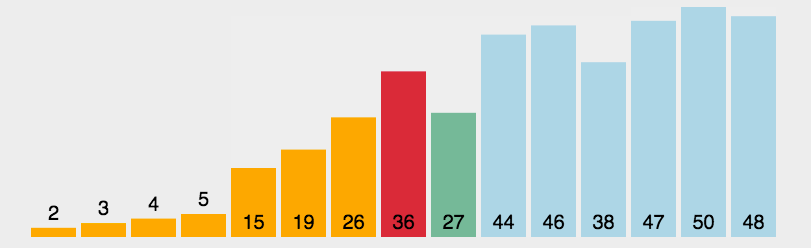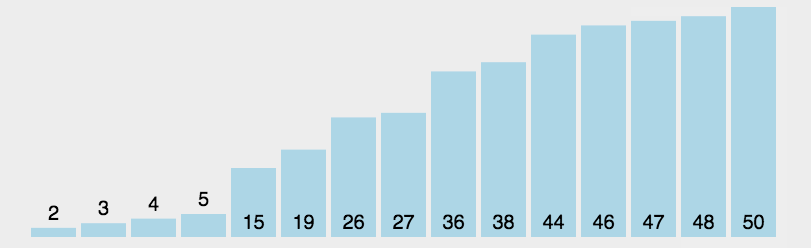
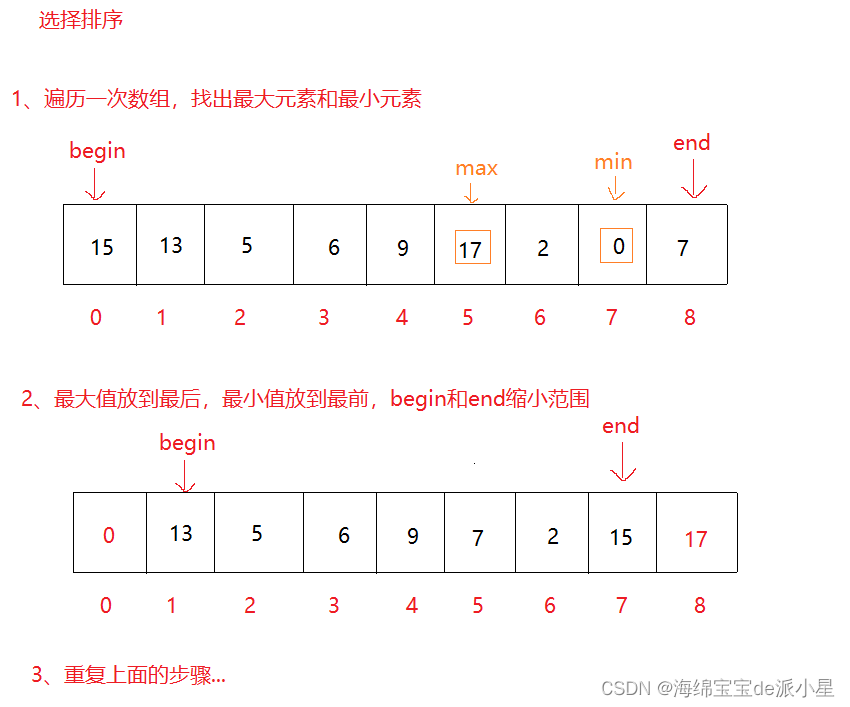
这里需要注意一点是,maxi可能会和begin重叠,导致交换begin和min的时候产生bug,因此只需要在前面补充一下条件即可
void SelectSort(int* a, int n)
{
int begin = 0, end = n - 1;
while (begin < end)
{
int maxi = begin, mini = begin;
for (int i = begin; i <= end; i++)
{
if (a[i] > a[maxi])
{
maxi = i;
}
if (a[i] < a[mini])
{
mini = i;
}
}
Swap(&a[begin], &a[mini]);
// 如果maxi和begin重叠,修正一下即可
if (begin == maxi)
{
maxi = mini;
}
Swap(&a[end], &a[maxi]);
++begin;
--end;
}
}
堆排序
堆排序前面文章有过详细讲解,这里就不多赘述了
数据结构—手撕图解堆
直接上代码实现
void Swap(int* p, int* c)
{
int tmp = *p;
*p = *c;
*c = tmp;
}
void AdjustDown(int* a, int n, int parent)
{
int child = parent * 2 + 1;
while (child < n)
{
if (child + 1 < n && a[child + 1] > a[child])
{
child++;
}
if (a[parent] < a[child])
{
Swap(&a[parent], &a[child]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
void HeapSort(int* a, int n)
{
// 建堆
for (int i = (n - 2) / 2; i >= 0; i--)
{
AdjustDown(a, n, i);
}
// 堆排序
int end = n - 1;
while (end)
{
Swap(&a[0], &a[end]);
AdjustDown(a, end, 0);
end--;
}
}
交换排序
冒泡排序
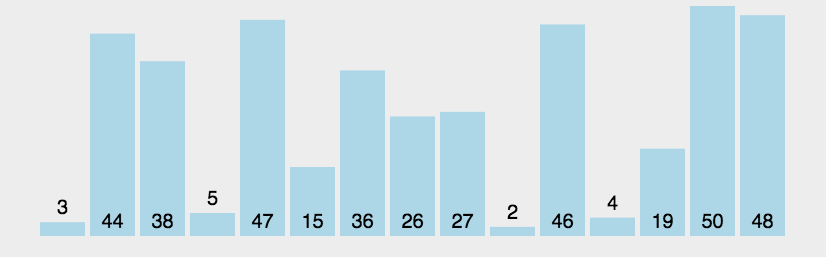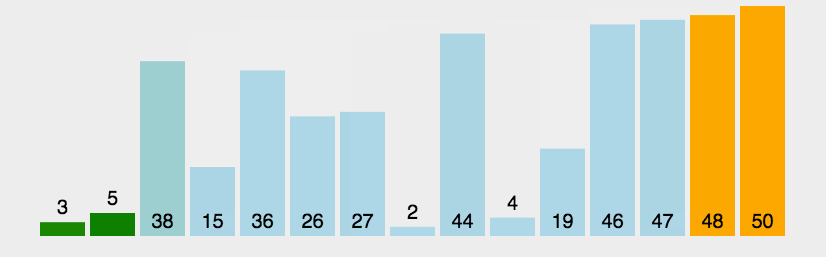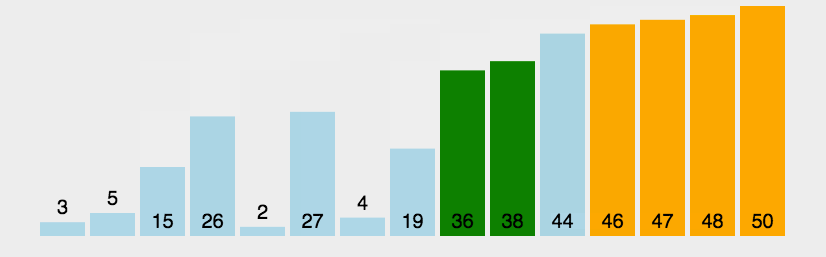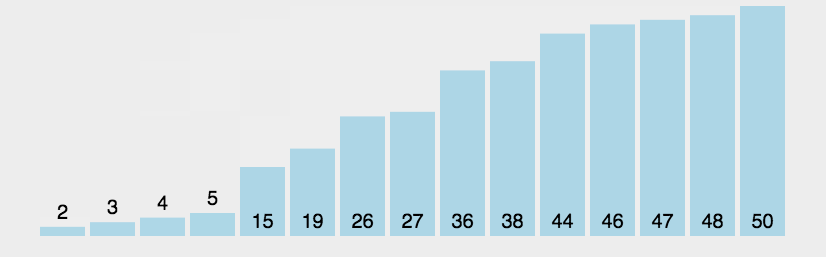
入门出学的第一个排序,效率很低
void BubbleSort(int* a, int n)
{
for (int i = 0; i < n - 1; i++)
{
int flag = 0;
for (int j = 0; j < n - i - 1; j++)
{
if (a[j] > a[j + 1])
{
flag = 1;
int tmp = a[j];
a[j] = a[j + 1];
a[j + 1] = tmp;
}
}
if (flag == 0)
{
break;
}
}
}
下面重点是对快速排序进行学习,快速排序正常来说是泛用性最广的排序算法
快速排序
快速排序是所有排序算法中速度最快的一个排序算法(在数据量很庞大的前提下),因此,很多库中自带的sort都是用快速排序做底层实现的,例如qsort和STL中的sort,因此,学习好它是很有必要的
首先说明它的基本思想
基本思路是,选定一个元素为key,经过一系列算法让原本数组中比key小的数据在key的左边,比key大的数据在key的右边,然后递归进入key的左边,在递归函数中重复这个操作,最后就能完成排序,那么第一个关键点就是如何实现让以key为分界点,左右分别是比它大和比它小的?
关于这个算法有很多版本,我们一一介绍
hoare版
快速排序的创始人就是hoare,作为快速排序的祖师爷,hoare在研究快速排序自然写出了对应的算法,那么我们当然要先学习最经典的算法
下面展示hoare算法的示意图
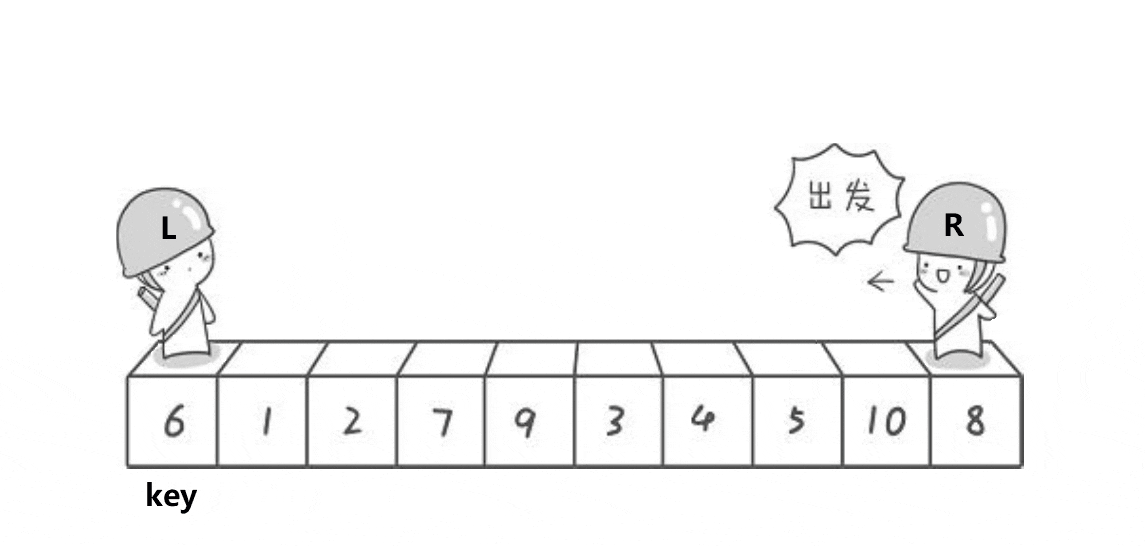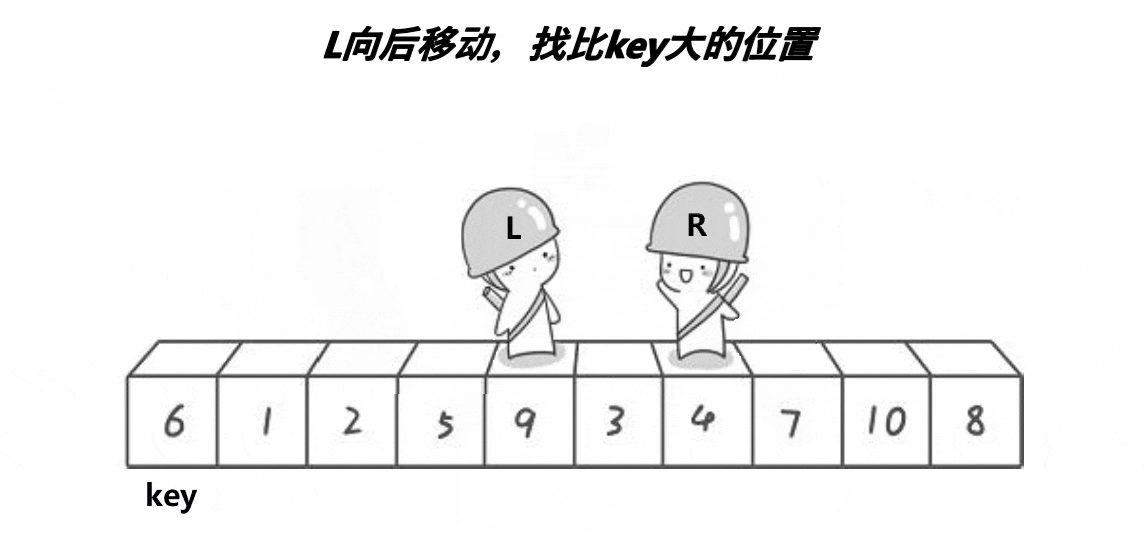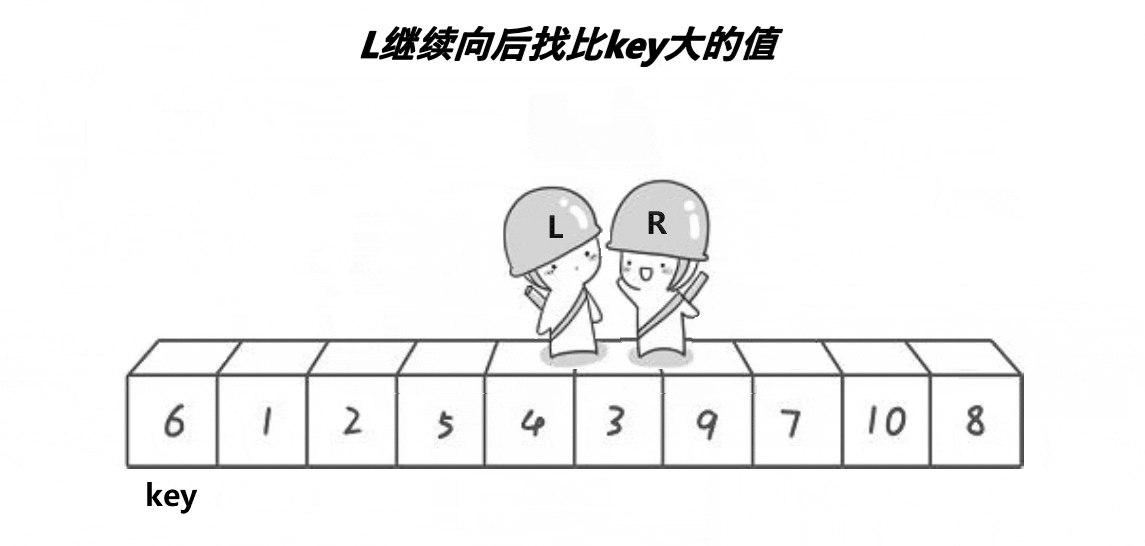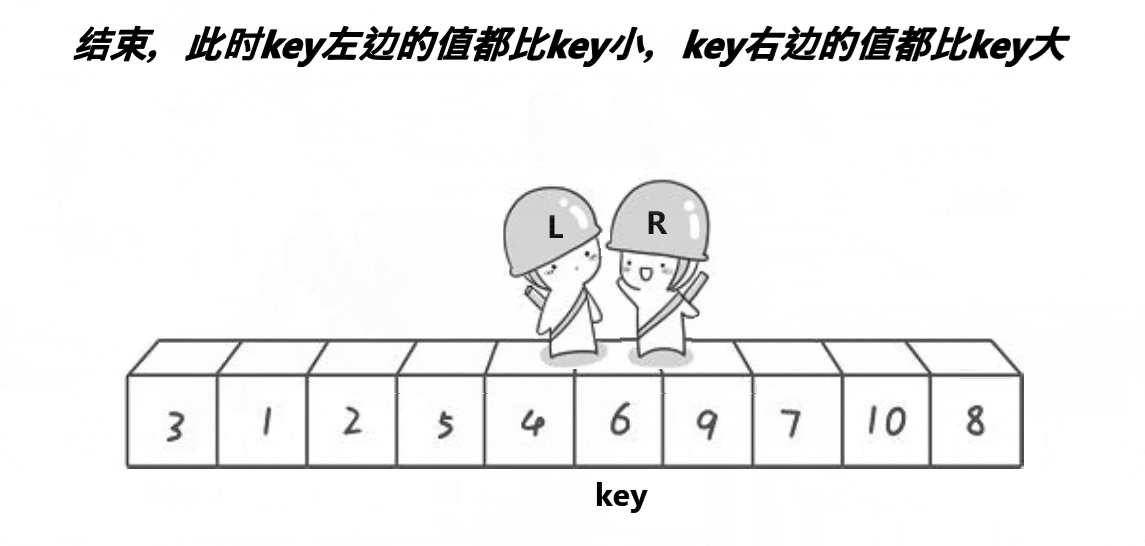
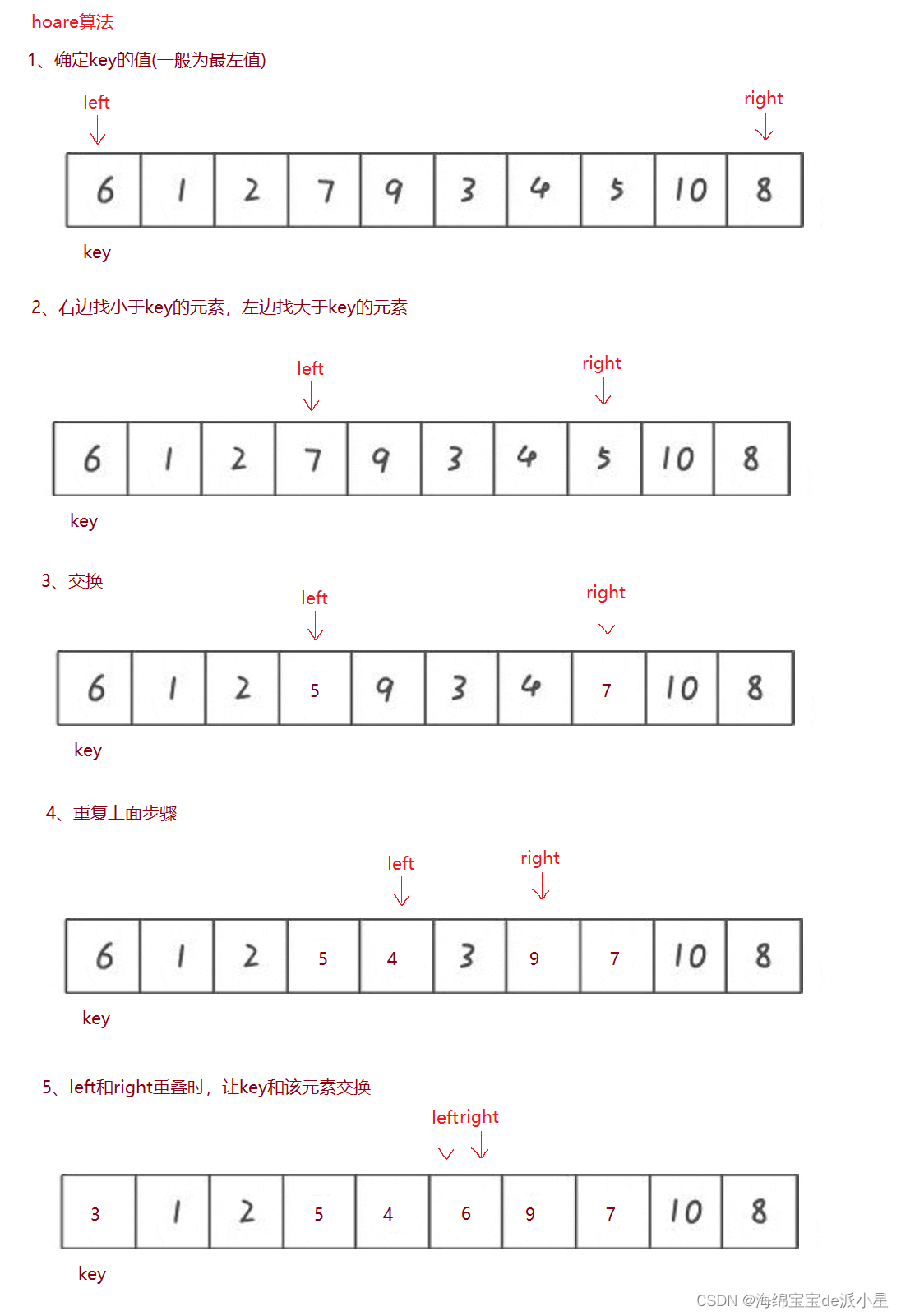
看完演绎图和上面的流程图,大概可以理解hoare算法的基本思路,但其实还有一些问题,比如最后交换的元素(上图中为3) 一定比key小吗?比key大难道不会让大的元素到key的左边吗?
解释上述问题的原因
其实问题的原因就在于left和right谁先走的问题,在上面算法中是让right先走,这是为什么?
我们假设中间的元素不是3,而是8 (大于key的都可以) 那么,当right继续向前走的时候就会跳过8,继续向前找,最后最坏的结果会找到left,而left对应的是和前面交换后的比key小的元素,因此这里只要是right先走,最终和right和left相遇的位置一定比key小!
这个算法其实并不好写,需要控制的变量和问题很多,实现过程如下
int PartSort1(int* a, int left, int right)
{
int keyi = left;
while (left < right)
{
while (left < right && a[right] >= a[keyi])
{
right--;
}
while (left < right && a[left] <= a[keyi])
{
left++;
}
Swap(&a[left], &a[right]);
}
Swap(&a[keyi], &a[left]);
return left;
}
注意点
- keyi的选取是left而不是0,因为后面递归的时候最左边的元素下标不一定是0
- while循环向前/向后寻找时要随时判断left有没有小于right,防止越界
- 返回的是左值,这个左值就是下一次的左边界或右边界、
快速排序的实现
void QuickSort(int* a, int begin, int end)
{
if (begin >= end)
{
return;
}
int keyi = PartSort1(a, begin, end);
QuickSort(a, begin, keyi - 1);
QuickSort(a, keyi + 1, end);
}
后续的三种写法只需要替换掉PartSort1即可
挖坑法
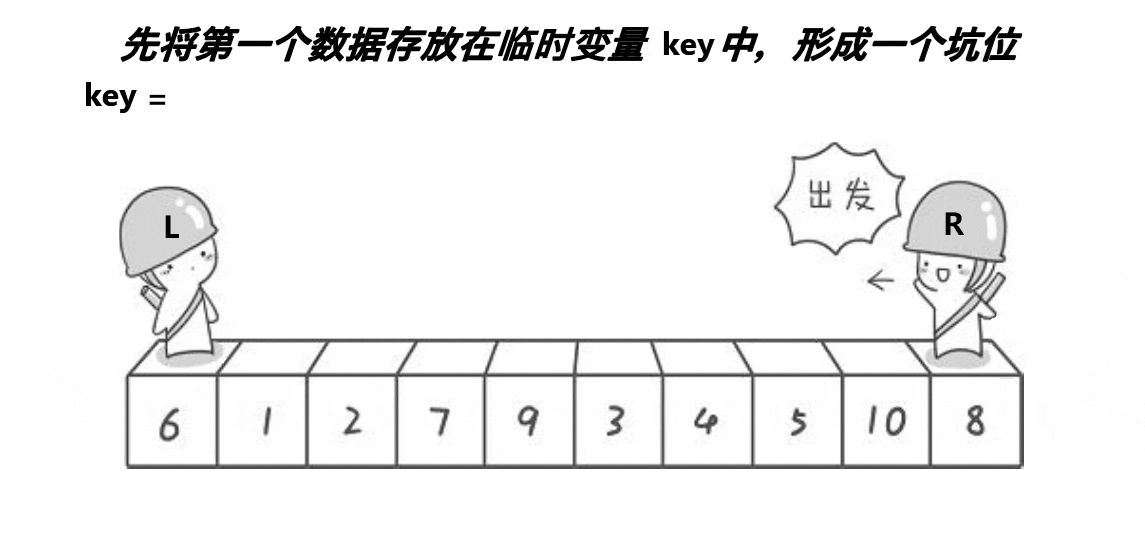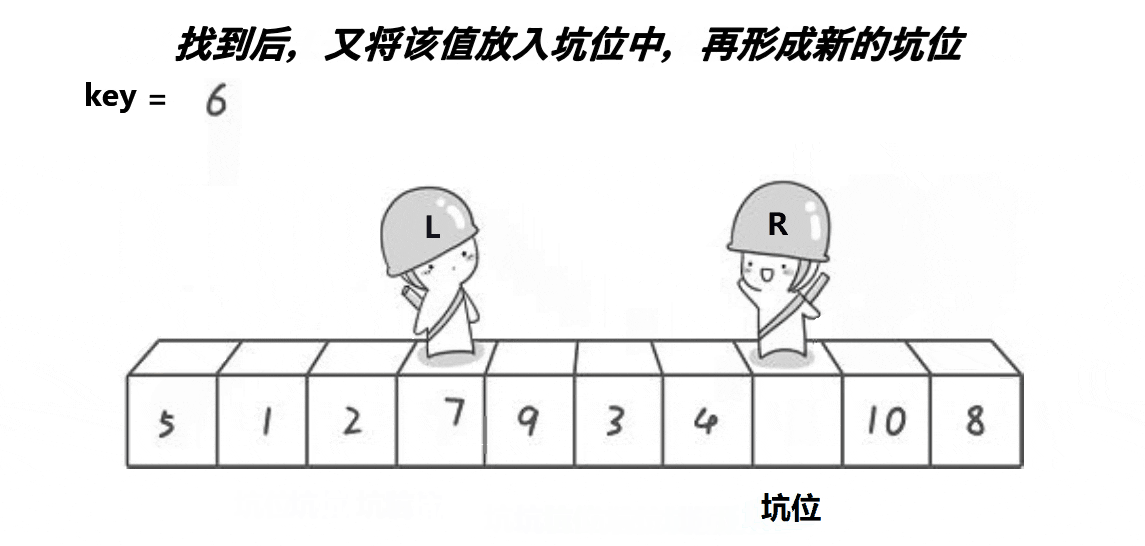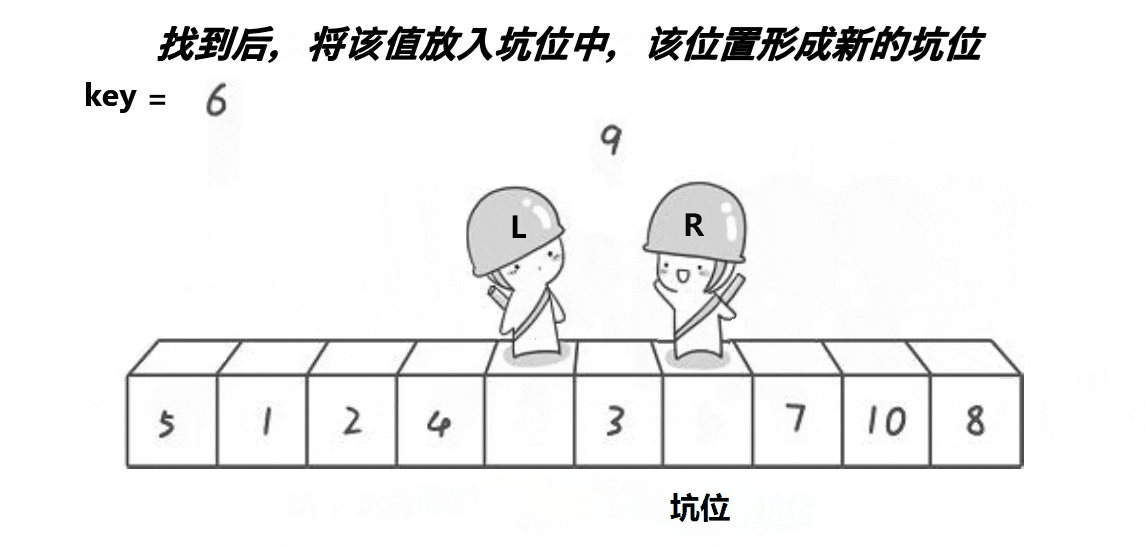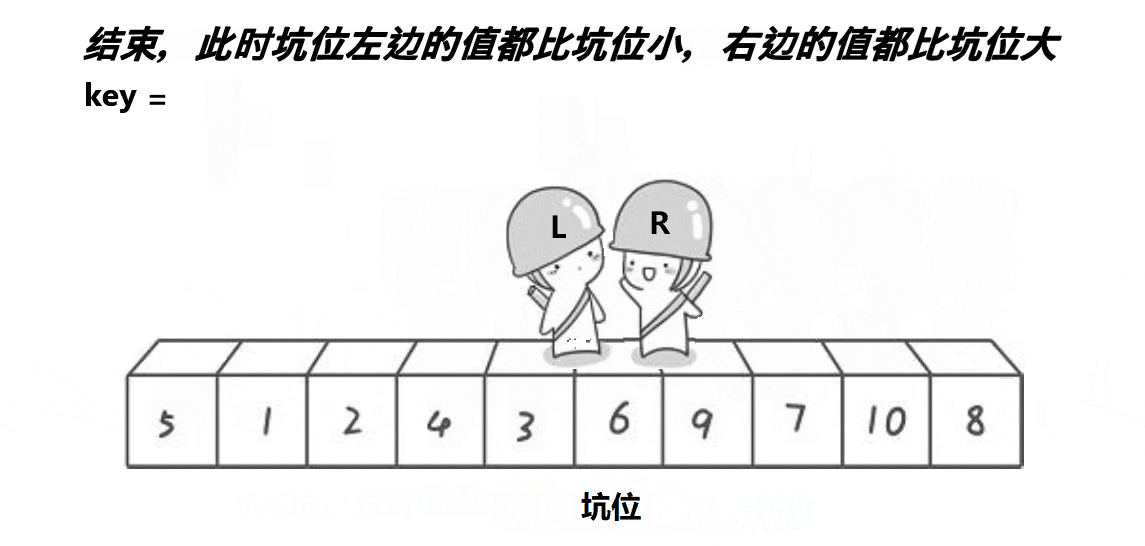

代码实现如下:
int PartSort2(int* a, int left, int right)
{
int key = a[left];
int hole = left;
while (left < right)
{
while (left<right && a[right]>= key)
{
right--;
}
a[hole] = a[right];
hole = right;
while (left < right && a[left] <= key)
{
left++;
}
a[hole] = a[left];
hole = left;
}
a[hole] = key;
return hole;
}
void QuickSort(int* a, int begin, int end)
{
if (begin >= end)
{
return;
}
int keyi = PartSort2(a, begin, end);
QuickSort(a, begin, keyi - 1);
QuickSort(a, keyi + 1, end);
}
这个实现很简单,没有需要额外注意,相较第一个算法来说更容易理解一些
前后指针法
实现原理如下图所示
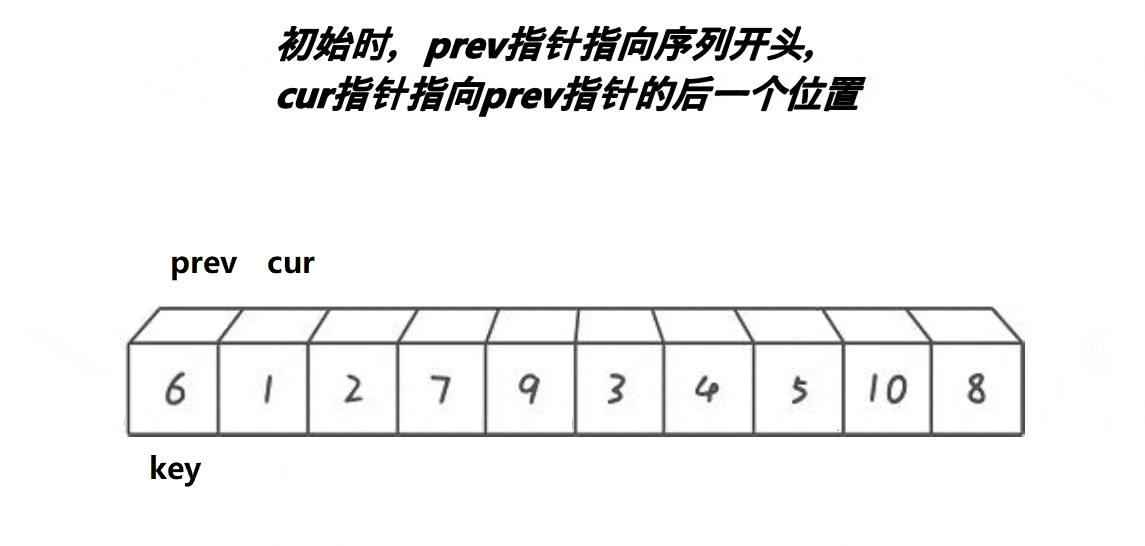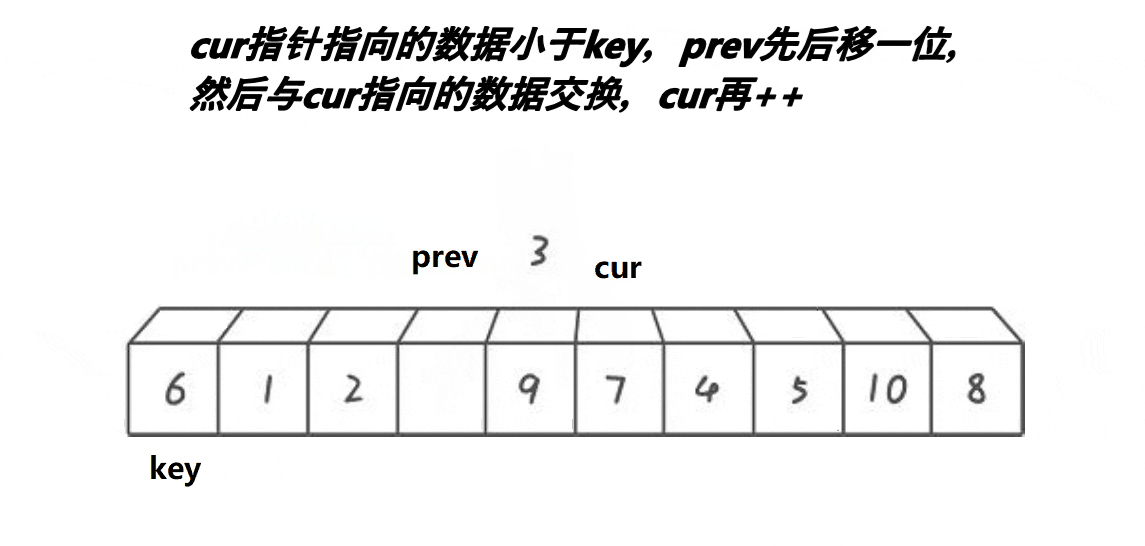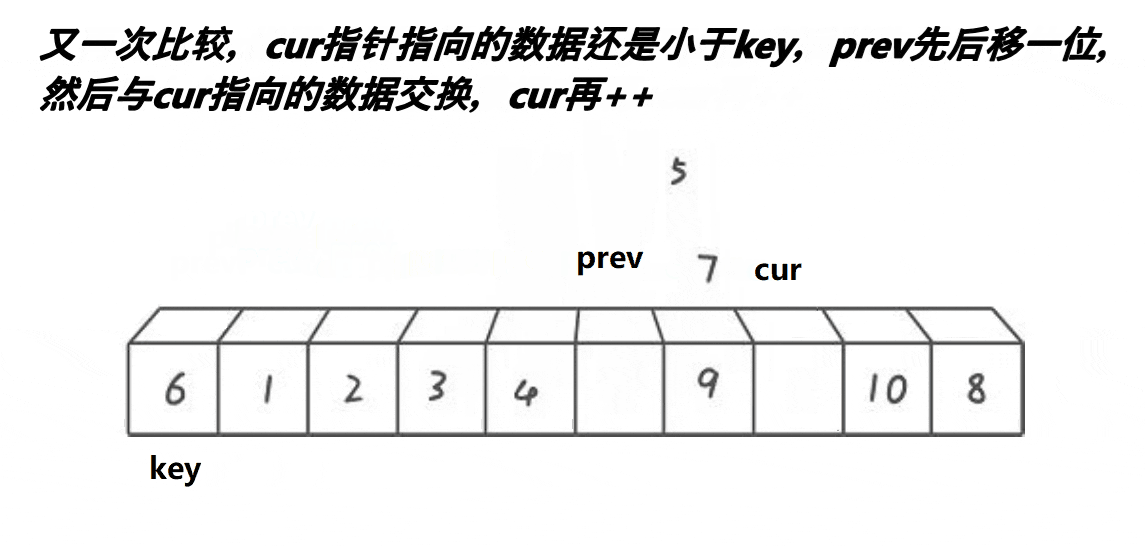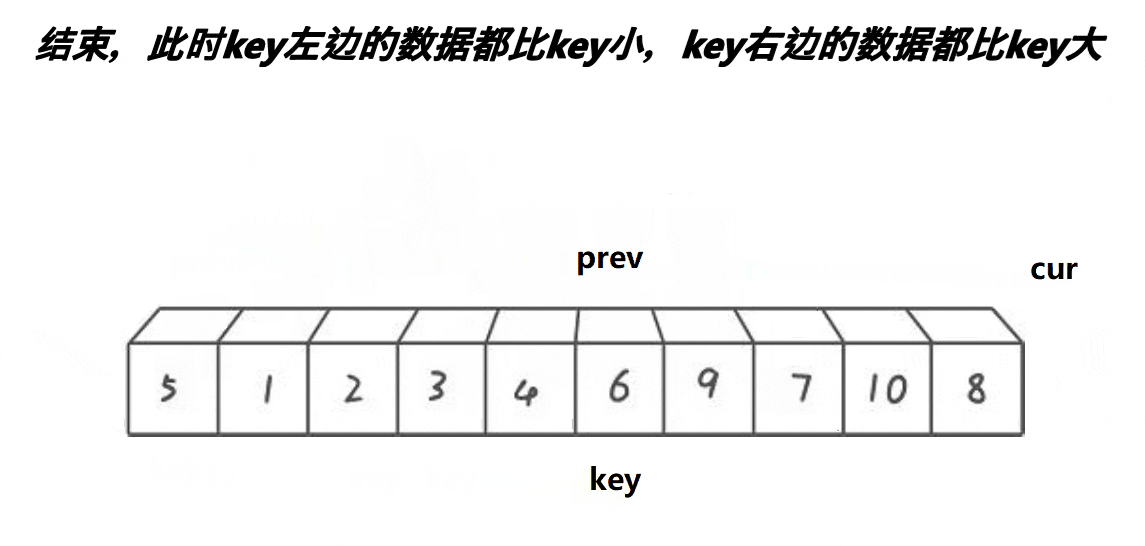

代码实现逻辑如下
int PartSort3(int* a, int left, int right)
{
int cur = left+1;
int prev = left;
int keyi = left;
while (cur <= right)
{
if (a[cur] < a[keyi])
{
++prev;
Swap(&a[prev], &a[cur]);
}
cur++;
}
Swap(&a[prev], &a[keyi]);
return prev;
}
void QuickSort(int* a, int begin, int end)
{
if (begin >= end)
{
return;
}
int keyi = PartSort3(a, begin, end);
QuickSort(a, begin, keyi - 1);
QuickSort(a, keyi + 1, end);
}
实际上是prev找cur,如果cur指针对应的值小于key,那么就++prev再交换,否则cur就继续前进,这样就能使得cur和prev之间的数据全部为比key大的数据
快速排序的递归展开图
了解了快速排序的工作原理,独立画出它的递归展开图有助于了解它的工作原理
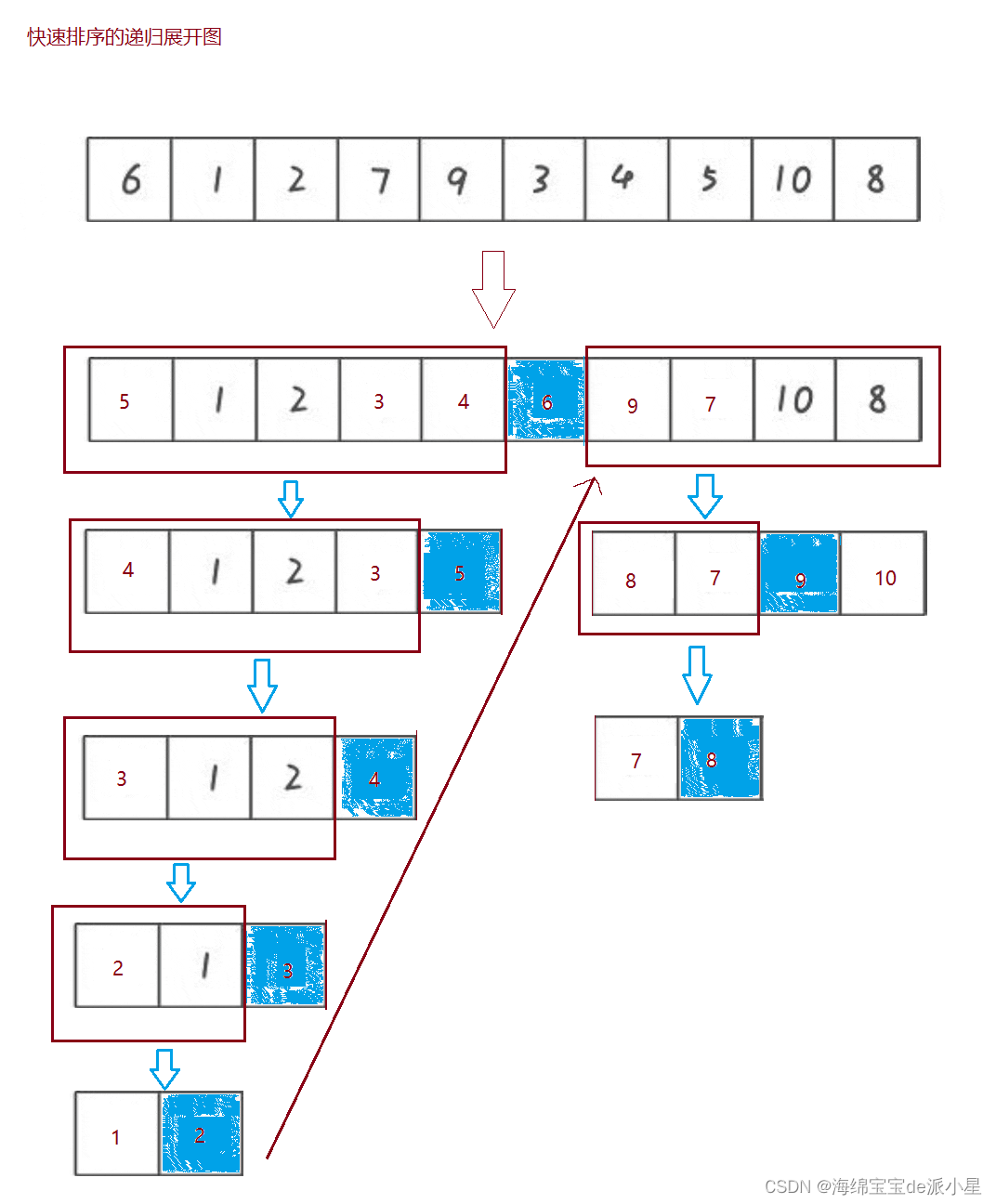
快速排序的优化
快速排序确实是在很多方面都很优秀的排序,但是仅仅用上述的代码并不能完全解决问题,假设现在给的序列是一个按升序排列的序列,那么此时我们选取的key是最小的数据,时间复杂度是O(N^2),但如果每次选取的数据恰好是中位数,那么就是整个数据最高效的方式,时间复杂度是O(NlogN),因此如何优化?
常见的优化有三数取中法和递归到小的子区间选取插入排序法
三数取中法
顾名思义,就是取开头,末尾和中间的三个数,选这三个数中最中间的一个,让这个数作为key
int GetMid(int* a, int left, int right)
{
int midi = (left + right) / 2;
if (a[left] < a[midi])
{
if (a[midi] < a[right])
{
return midi;
}
else if (a[left] > a[right])
{
return left;
}
else
{
return right;
}
}
else // a[left] > a[midi]
{
if (a[midi] > a[right])
{
return midi;
}
else if (a[left] < a[right])
{
return left;
}
else
{
return right;
}
}
}
int PartSort1(int* a, int left, int right)
{
int midi = GetMid(a, left, right);
Swap(&a[midi], &a[left]);
int keyi = left;
while (left < right)
{
while (left < right && a[right] >= a[keyi])
{
right--;
}
while (left < right && a[left] <= a[keyi])
{
left++;
}
Swap(&a[left], &a[right]);
}
Swap(&a[keyi], &a[left]);
return left;
}
int PartSort2(int* a, int left, int right)
{
int midi = GetMid(a, left, right);
Swap(&a[midi], &a[left]);
int key = a[left];
int hole = left;
while (left < right)
{
while (left < right && a[right] >= key)
{
right--;
}
a[hole] = a[right];
hole = right;
while (left < right && a[left] <= key)
{
left++;
}
a[hole] = a[left];
hole = left;
}
a[hole] = key;
return hole;
}
int PartSort3(int* a, int left, int right)
{
int midi = GetMid(a, left, right);
Swap(&a[midi], &a[left]);
int cur = left+1;
int prev = left;
int keyi = left;
while (cur <= right)
{
if (a[cur] < a[keyi])
{
++prev;
Swap(&a[prev], &a[cur]);
}
cur++;
}
Swap(&a[prev], &a[keyi]);
return prev;
}
void QuickSort(int* a, int begin, int end)
{
if (begin >= end)
{
return;
}
int keyi = PartSort1(a, begin, end);
QuickSort(a, begin, keyi - 1);
QuickSort(a, keyi + 1, end);
}
快速排序的非递归实现
快速排序是利用递归实现的,而凡是递归就有可能爆栈的情况出现,因此这里要准备快速排序的非递归实现方法
非递归实现是借助栈实现的,栈是在堆上malloc实现的,栈区一般在几十Mb左右,而堆区有几G左右的空间,在堆上完成操作是没有问题的
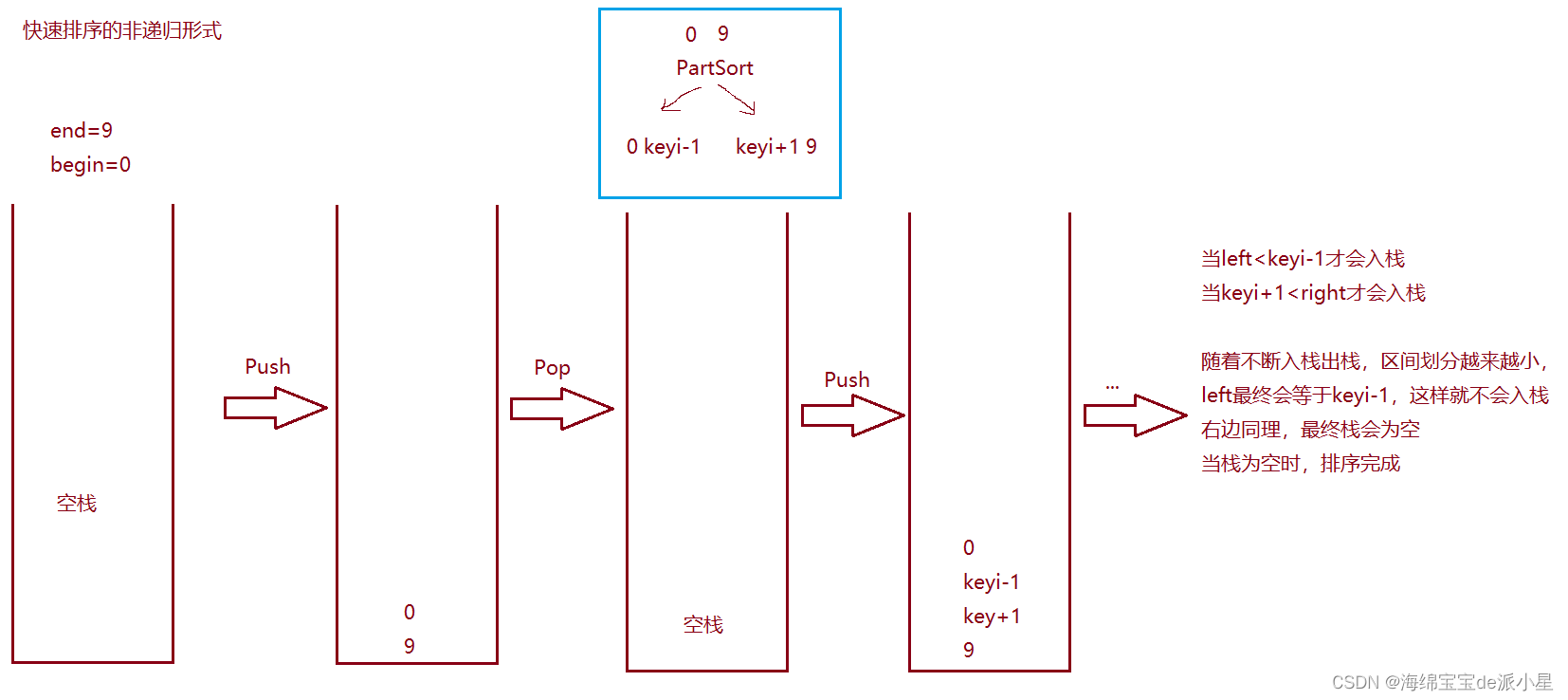
当left<keyi-1才会入栈,当keyi+1<right才会入栈
随着不断入栈出栈,区间划分越来越小,left最终会等于keyi-1,这样就不会入栈,右边同理,不入栈只出栈,最终栈会为空,当栈为空时,排序完成
归并排序
归并排序的排序原理如下:
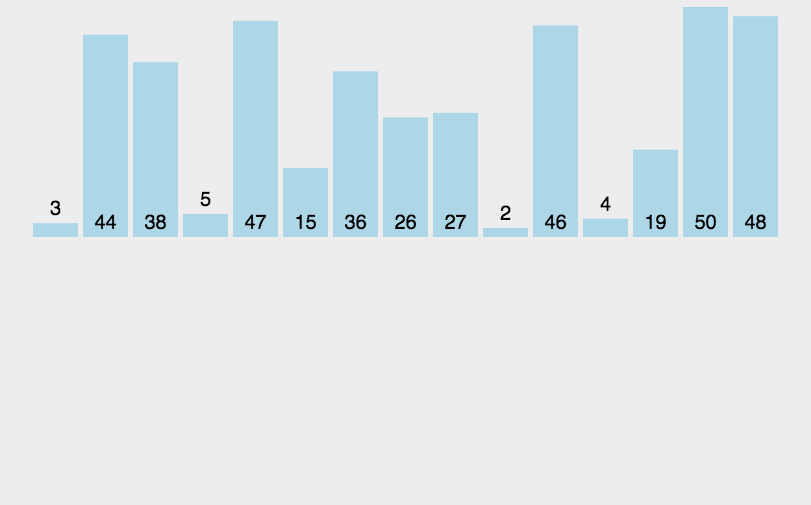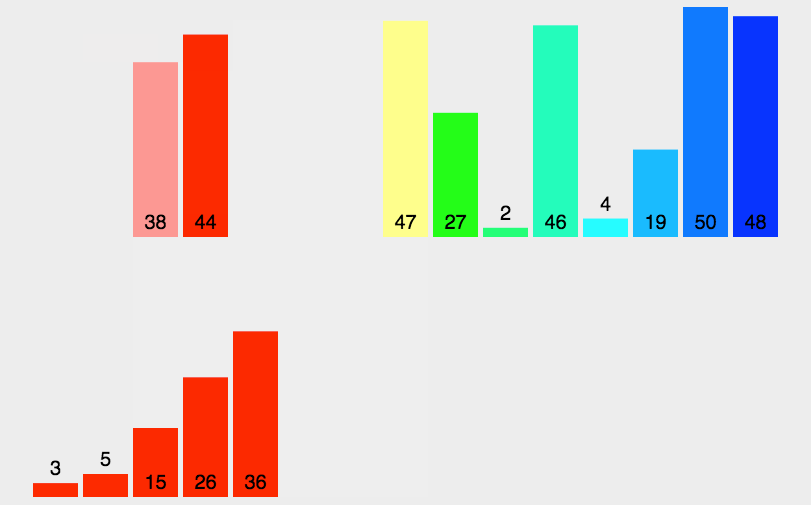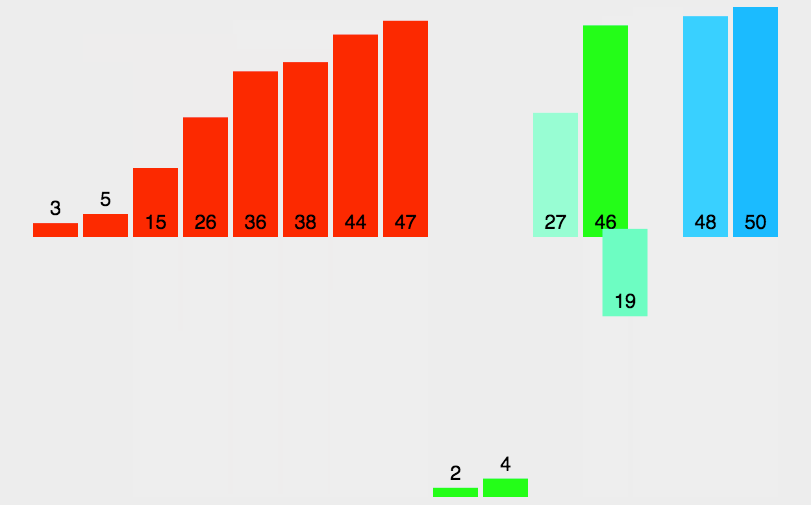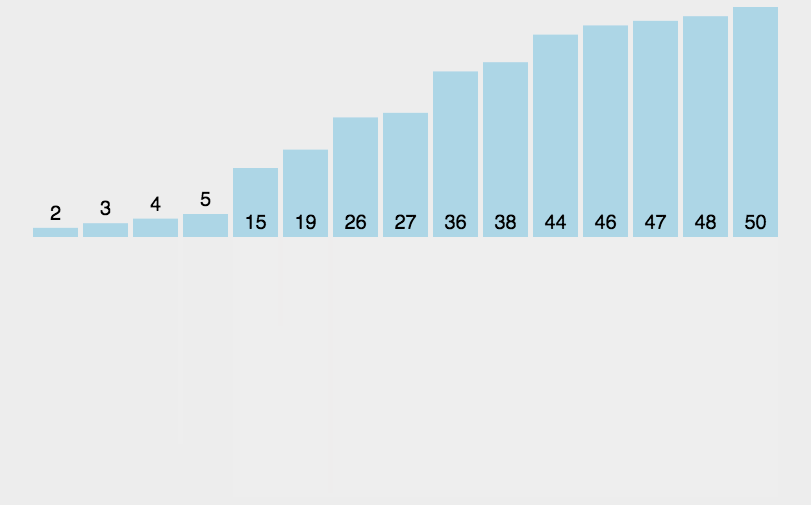
从中可以看出,归并排序的原理就是把一整个大的,无序的数组分解成小数组,直到分到数组中只有一个数,再把数组组装成有序的数组,再把组装成有序的两个数组合并成有序数组,再让这个有序数组和另外一个合并…依次递归,这样就和二叉树一样递归成了一个合适的数组

代码实现如下:
void _MergeSort(int* a, int begin, int end, int* tmp)
{
if (begin == end)
return;
int mid = (begin + end) / 2;
_MergeSort(a, begin, mid, tmp);
_MergeSort(a, mid + 1, end, tmp);
int begin1 = begin, end1 = mid;
int begin2 = mid + 1, end2 = end;
int i = begin;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[i++] = a[begin1++];
}
else
{
tmp[i++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[i++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = a[begin2++];
}
memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));
}
void MergeSort(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
_MergeSort(a, 0, n - 1, tmp);
free(tmp);
}