1.盛水最多的容器(11)

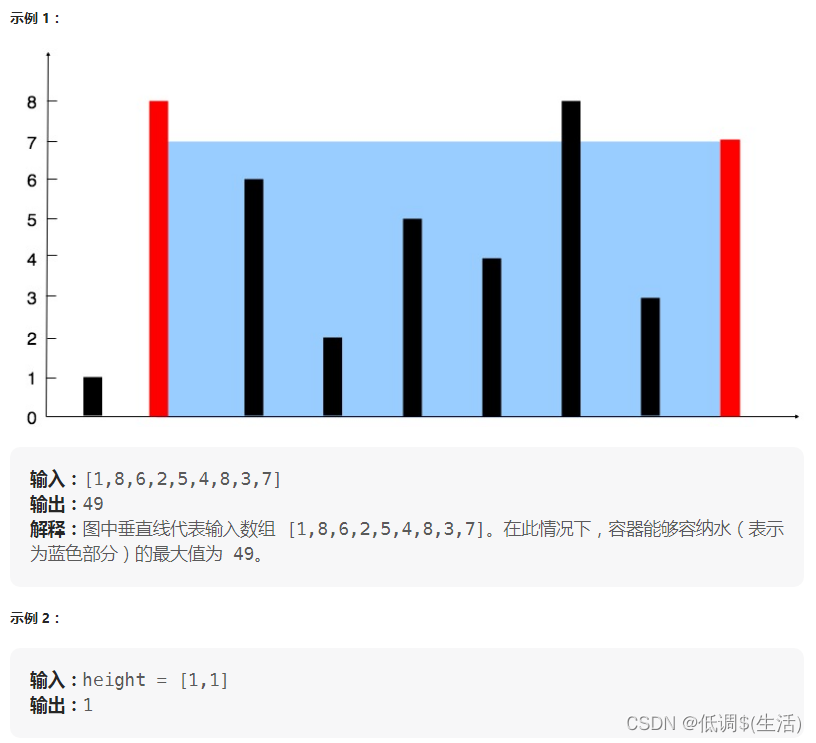
给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

说明：你不能倾斜容器。

 方法一(双端点法)

解题思路:

我刚开始想到的是暴力双端点法,结果发现运行时间超过限制,然后看了力友们的解析,恍然大悟.

首先设置双指针,左指针指最开头,右指针指最右,然后遍历,每次求最小高度和面积.然后判断左右指针谁指的数最小,舍弃小的,指针变化.

原理:一个长方形,宽变小,高度不变的话,则面积变小,若高度改变的话,则面积有可能增加,所以每次舍弃最小边界高度.

class Solution {
    public int maxArea(int[] height) {
        int s=0,left=0,right=height.length-1,minHeight=0,tempS;
        while(left<right){
            minHeight=(height[left]>=height[right]?height[right]:height[left]);
            tempS=(right-left)*minHeight;
            s=(s>=tempS?s:tempS);
            if(height[left]>=height[right]){
               right--;
            }else{
                left++;
            }
        }
        return s;
    }
}

2.整数转罗马数字(12)

罗马数字包含以下七种字符： I， V， X， L，C，D 和 M。

字符          数值
I             1
V             5
X             10
L             50
C             100
D             500
M             1000

例如， 罗马数字 2 写做 II ，即为两个并列的 1。12 写做 XII ，即为 X + II 。 27 写做  XXVII, 即为 XX + V + II 。

通常情况下，罗马数字中小的数字在大的数字的右边。但也存在特例，例如 4 不写做 IIII，而是 IV。数字 1 在数字 5 的左边，所表示的数等于大数 5 减小数 1 得到的数值 4 。同样地，数字 9 表示为 IX。这个特殊的规则只适用于以下六种情况：

• I 可以放在 V (5) 和 X (10) 的左边，来表示 4 和 9。
• X 可以放在 L (50) 和 C (100) 的左边，来表示 40 和 90。 
• C 可以放在 D (500) 和 M (1000) 的左边，来表示 400 和 900。

给你一个整数，将其转为罗马数字。

方法一(贪心算法)

在力扣中看到的这种算法，只能说太妙了，我怎么没想到这样减法，只能说我还有很长的路要走。

思路：尽可能使用最大字符来替换

class Solution {
    public String intToRoman(int num) {
       int[] nums={1000,900,500,400,100,90,50,40,10,9,5,4,1};
       String[] romans={"M","CM","D","CD","C","XC","L","XL","X","IX","V","IV","I"};
       StringBuilder stringBuilder=new StringBuilder();
       int index = 0;
        while (index < nums.length) {
            // 特别注意：这里是等号
            while (num >= nums[index]) {
                stringBuilder.append(romans[index]);
                num -= nums[index];
            }
            index++;
        }
        return stringBuilder.toString();
    }
}