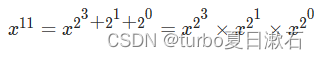目录

剑指 Offer 16. 数值的整数次方

题解：

知识点：

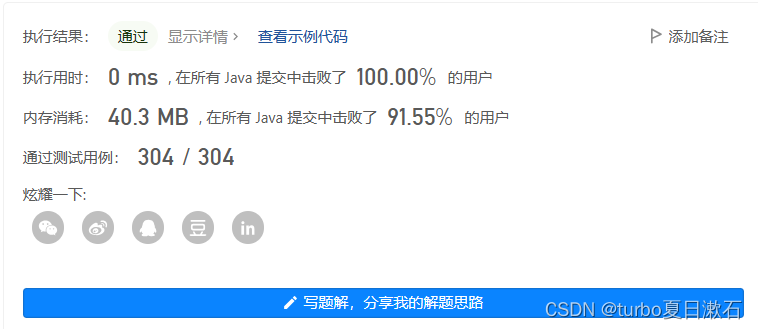
代码：

结果：

---

实现 pow(x, n) ，即计算 x 的 n 次幂函数（即，xn）。不得使用库函数，同时不需要考虑大数问题。

示例 1：

输入：x = 2.00000, n = 10
输出：1024.00000
示例 2：

输入：x = 2.10000, n = 3
输出：9.26100
示例 3：

输入：x = 2.00000, n = -2
输出：0.25000
解释：2-2 = 1/22 = 1/4 = 0.25
 

提示：

-100.0 < x < 100.0
-231 <= n <= 231-1
n 是一个整数
要么 x 不为零，要么 n > 0 。
-104 <= xn <= 104

题解：

快速幂的思想：

将指数11 可以转成二进制数1011，则原来的式子可以转化成

 

此时只运算了3次乘积，时间复杂度降至O(logn)

1. 首先判断底数x是否为0，如果是0则直接返回0
2. 将指数n转化为长整型变量b，避免在处理负数时出现溢出问题
3. 初始化结果res为1.0
4. 如果指数b小于0，说明底数x取倒数，同时将指数b取相反数
5. 进入循环，当指数b大于0时继续执行循环体内的操作
6. 使用位运算判断指数b的最后一位是否为1，如果是1则将结果res乘以底数x
7. 更新底数x为x的平方
8. 将指数b右移一位，相当于将其除以2
9. 循环结束后返回结果res

利用了位运算来判断指数的最后一位是否为1，从而确定是否需要乘以底数x。同时，通过不断平方底数x和右移指数b，实现了快速求幂的效果

知识点：

位运算：

位运算是计算机中对二进制数据进行操作的一种运算方式。它直接在二进制位上进行操作，可以高效地进行一些常见的运算，如与、或、异或和移位等。

以下是一些常用的位运算符：

• 与运算（&）：按位进行与运算，两个位都为1时结果为1，否则为0。
• 或运算（|）：按位进行或运算，两个位中只要有一个为1时结果为1，否则为0。
• 异或运算（^）：按位进行异或运算，两个位相同为0，不同为1。
• 非运算（~）：按位进行非运算，将每个位取反。
• 左移运算（<<）：将二进制数向左移动指定的位数，相当于乘以2的幂。
• 右移运算（>>）：将二进制数向右移动指定的位数，相当于除以2的幂。

位运算在计算机领域的应用非常广泛，包括但不限于以下方面：

• 位掩码：使用位运算来创建、修改和查询特定位的值，用于标记或设置某些状态。
• 压缩算法：利用位运算来压缩数据，减少存储空间。
• 加密和解密：位运算可用于实现加密和解密算法中的位级操作。
• 优化算法：某些算法可以使用位运算进行优化，例如快速求幂、快速排序等。

代码：

class Solution {
    public double myPow(double x, int n) {
        if(x==0) return x;
        long b=n;//将指数n转化为长整型变量b，避免在处理负数时出现溢出问题。
        //负数幂
        if(b<0){
            x=1/x;
            b=-b;
        }
        double res=1.0;
        //快速幂思想（二进制角度）
        while(b>0){
            if((b&1)==1){
                res*=x;
            }
            x*=x;
            b>>=1;
        }
        return res;
    }
}

结果：