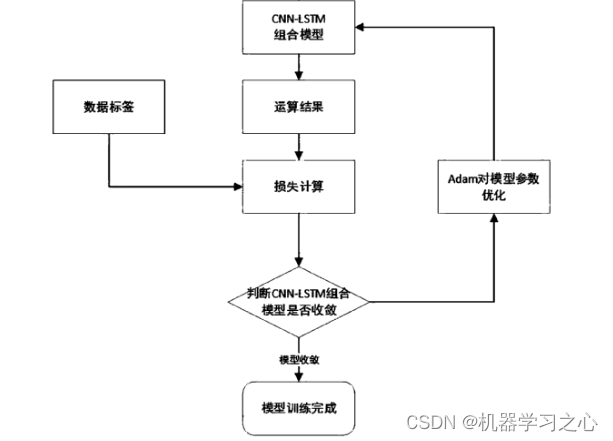
【时间序列预测 2023 ICLR】TimesNet

论文题目：TIMESNET: TEMPORAL 2D-VARIATION MODELING FOR GENERAL TIME SERIES ANALYSIS

中文题目：TimesNet:用于一般时间序列分析的时态二维变异建模

论文链接：https://arxiv.org/abs/2210.02186

论文代码：https://github.com/thuml/TimesNet

论文团队：清华大学

发表时间：2022年10月

DOI:

引用：

引用数：18(截止时间：2023年7月26号)

摘要

时间序列分析在天气预报、异常检测、行为识别等广泛应用中具有重要意义。 本文重点研究了时间变化建模，这是广泛分析任务的共同关键问题。 以往的方法试图直接从一维时间序列中完成这一任务，但由于复杂的时间模式，这是极具挑战性的。 在观测时间序列多周期的基础上，我们将复杂的时间变化分解为多重的周期内和周期间变化。 为了解决一维时间序列在表示能力上的局限性，我们将一维时间序列转化为一组基于多个周期的二维张量，从而将时间变化的分析扩展到二维空间。 该变换可以将周期内和周期间的变化分别嵌入到二维张量的列和行中，使二维变化易于用二维核模型来模拟。 在技术上，我们提出了TimesNet和TimesBlock作为时间序列分析的任务通用主干网。 TimesBlock能够自适应地发现多周期性，并通过参数有效的起始块从变换后的二维张量中提取复杂的时间变化。 我们提出的TimesNet在主流时间序列分析任务中实现了一致的最新技术，包括短期和长期预测、估算、分类和异常检测。

1. 简介

时间序列分析在广泛的现实世界应用中得到了广泛的应用，如用于天气预报的气象因子预测（Wu et al.，2021)、用于数据挖掘的缺失数据归算(Friedman，1962)、用于工业维护的监测数据异常检测（Xu et al.，2021)和用于动作识别的轨迹分类（Franceschi et al.，2019)。 由于其巨大的实用价值，时间序列分析受到了极大的关注(Lim&Zohren，2021)。

不同于其他类型的顺序数据，如语言或视频，时间序列是连续记录的，每个时间点只保存一些标量。 由于单一的时间点往往不能提供丰富的语义信息，许多研究都集中在时间序列的时间变化上，因为时间变化具有更丰富的信息量，能够反映时间序列的连续性、周期性、趋势性等内在特性。然而，现实世界的时间序列的变化往往涉及复杂的时间模式，其中多种变化（如上升、下降、上升等）相互混合和重叠，使得时间变化建模具有极大的挑战性。

特别是在深度学习领域，利用深度模型强大的非线性建模能力，人们提出了许多捕捉真实时间序列中复杂时间变化的方法。 一类方法基于马尔可夫假设采用递归神经网络(RNN)对连续时间点进行建模（Hochreiter&Schmidhuber,1997；Lai et al.，2018；Shen et al.，2020）。 然而，这些方法通常无法捕捉长期依赖关系，并且它们的作用受到顺序计算范式的影响。 另一类方法利用沿时间维的卷积神经网络(TCN)来提取变异信息（Franceschi et al.，2019；He&Zhao,2019）。 此外，由于一维卷积核的局部性，它们只能模拟相邻时间点之间的变化，因而在长期相关性方面仍然失败。 最近，具有注意力机制的变压器被广泛应用于序列建模（Brown et al.，2020；Dosovitskiy et al.，2021；Liu et al.，2021b)。 在时间序列分析中，许多基于Transformer的模型采用注意力机制或其变体来捕捉时间点之间的时间依赖关系（Li et al.，2019；Kitaev et al.，2020；Zhou et al.，2021；2022）。 但是，由于时间依赖关系在复杂的时间模式中会被严重遮蔽，注意力机制很难直接从分散的时间点中找出可靠的依赖关系（Wu et al.，2021)。

本文从多周期这一新的维度对时间序列进行分析，以解决复杂的时间变化问题。 首先，我们观察到现实世界的时间序列通常具有多周期性，例如天气观测的日变化和年变化，电力消费的周变化和季度变化。 这些多个周期相互重叠和相互作用，使得变异建模变得棘手。 其次，对于每一个周期，我们发现每一个时间点的变化不仅受其邻近区域的时间模式的影响，而且与相邻周期的变化密切相关。 为了清楚起见，我们将这两种时间变化分别命名为周期内变化和周期间变化。 前者表示一个时期内的短期时间模式。 后者可以反映连续不同时期的长期趋势。 注意，对于没有明显周期性的时间序列，其变化将主要由周期内变化所控制，并与周期长度为无限长的时间序列等效。

由于不同的周期会导致不同的周期内和周期间的变化，多周期自然可以导出一个模块化的时间变化建模体系结构，在该体系结构中，我们可以在一个模块中捕获由某个周期导出的变化。 此外，该设计使复杂的时态模式得以分离，有利于时态变化建模。 然而值得注意的是，一维时间序列很难同时显式地呈现两种不同类型的变化。 为了解决这一障碍，我们将时间变化的分析扩展到2D空间。 具体地说，如图1所示，我们可以将一维时间序列重塑为一个二维张量，其中每列包含一个周期内的时间点，每行包含不同周期中同一相位的时间点。 因此，通过将一维时间序列转化为一组二维张量，可以突破原来一维空间中表示能力的瓶颈，成功地将周期内变化和周期间变化统一到二维空间中，得到时间上的二维变化。

在技术上，基于上述动机，我们超越了以往的研究框架，提出了TimesNet作为一种新的时间序列分析的任务通用模型。 通过TimesBlock的支持，TimesNet可以发现时间序列的多周期性，并在模块化的体系结构中捕获相应的时间变化。 具体而言，TimesBlock可以根据学习到的周期自适应地将一维时间序列转换为一组二维张量，并通过参数有效的起始块进一步捕获二维空间中的周期内和周期间变化。 通过实验，TimesNet在五个主流分析任务中达到了一致的最先进水平，包括短期和长期预测、估算、分类和异常检测。 我们的贡献概括为三个方面：

• 考虑到时间变化的多周期性以及周期内和周期间的复杂交互作用，我们提出了一种模块化的时间变化建模方法。 通过将一维时间序列转换到二维空间，我们可以同时呈现周期内和周期间的变化。

• 我们提出了带有TimesBlock的TimesNet，通过一个参数有效的起始块来发现多个周期，并从转换后的二维张量中捕获时间上的二维变化。

• 作为一个任务通用的基础模型，TimesNet在五个主流时间序列分析任务中实现了一致的最先进水平。 包括详细和有洞察力的可视化。

2. 相关工作

时间变化模型作为时间序列分析的一个关键问题已经得到了很好的研究。

许多经典方法假设时间变化遵循预定义的模式，如ARIMA (Anderson & Kendall, 1976)， Holt-Winter (Hyndman & Athanasopoulos, 2018)和Prophet (Taylor & Letham, 2018)。然而，现实世界中时间序列的变化通常过于复杂，无法用预定义的模式覆盖，这限制了这些经典方法的实际适用性。

近年来，针对时间建模提出了许多深度模型，如基于MLP、TCN、rnn的模型(Hochreiter & Schmidhuber, 1997;Lai et al.， 2018;Franceschi等，2019)。技术上，基于mlp的方法(Oreshkin等人，2019;查卢等人，2022年;曾等，2023;Zhang et al.， 2022)在时间维度上采用MLP，并将时间依赖性编码为MLP层的固定参数。基于tcn(2019)的方法通过沿着时间维度滑动的卷积核捕获时间变化。基于rnn的方法(Hochreiter & Schmidhuber, 1997;Lai et al.， 2018;Gu等人，2022)利用循环结构，通过时间步间的状态过渡隐式捕捉时间变化。请注意，这些方法都没有考虑由周期性衍生的时间二维变化，这是在本文中提出的。

此外，《Transformer》在时间序列预测方面表现出色(Zhou et al.， 2021;Liu et al.， 2021a;Wu等人，2021年;周等，2022)。利用注意机制，他们可以发现时间点之间的时间依赖性。特别是，Wu等人提出了带有自相关机制的自耦器，以捕捉基于学习周期的时序时序相关性。此外，为了解决复杂的时间模式，Autoformer还提出了一种深度分解体系结构，以获取输入序列的季节性和趋势部分。随后，FEDformer (Zhou et al.， 2022)采用专家混合设计增强季节趋势分解，并在频域内提出稀疏注意。与以往的方法不同，我们通过探索时间序列的多周期来解开复杂的时间模式，并首次通过公认的计算机视觉主干捕获二维空间中的时间二维变化。

值得注意的是，与以往的方法不同，我们不再局限于一个特定的分析任务，尝试提出一个任务通用的时间序列分析基础模型。

3. 方法

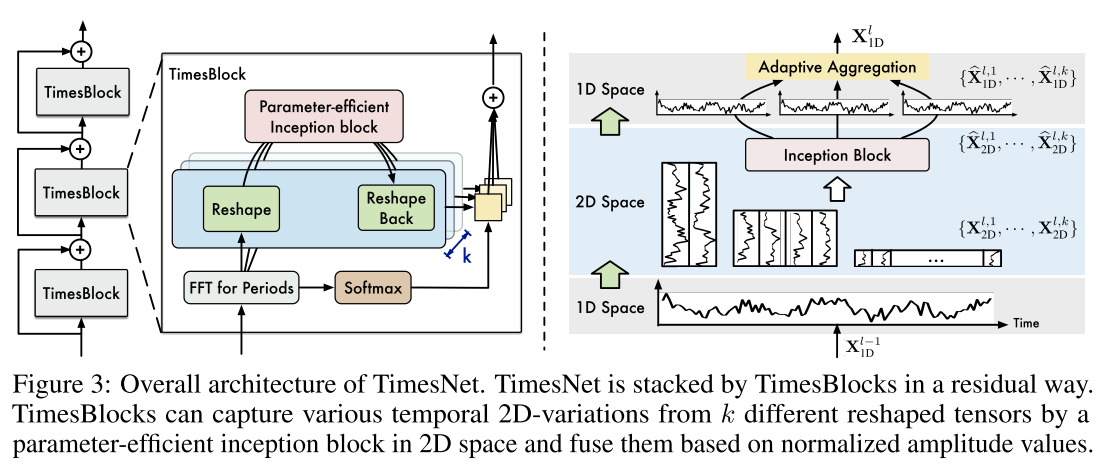
基于时间序列的多周期特性，我们提出了一种模块化的TimesNet来捕获不同周期的时间模式。 对于每一个周期，为了捕捉相应的周期内和周期间变化，我们在时间网中设计了一个时间块，它可以将一维时间序列转换到二维空间，并通过一个参数有效的起始块来同时建模两种类型的变化。

3.1 将一维变化转化为二维变化

如图1所示，每一个时间点同时包含两种与相邻区域和同一相位在不同时期之间的时间变化，即周内变化和周间变化。 然而，这种原始的一维时间序列结构只能反映相邻时间点之间的变化。 为了克服这一缺陷，我们探索了时间变化的二维结构，它可以显式地表达周期内和周期间的变化，从而在表征能力方面具有更大的优势，有利于后续的表征学习。

具体而言，对于具有$C$个记录变量的长度$T$时间序列，原始一维组织为${\mathbf{X}}_{\mathrm{lD}}\in {\mathbb{R}}^{T\times C}$。 为了表现周期间的变化，我们首先需要发现周期。 在技术上，我们用快速傅立叶变换(FFT)对时间序列进行频域分析如下：
A = A v g ( A m p ( F F T ( X I D ) ) ) , { f 1 , ⋯   , f k } = arg ⁡ T o p k ( A ) , p i = ⌈ T f i ⌉ , i ∈ { 1 , ⋯   , k } . \mathbf{A}=\mathrm{Avg}\left(\mathrm{Amp}\left(\mathrm{FFT}(\mathbf{X}_{\mathrm{ID}})\right)\right),\{f_{1},\cdots,f_{k}\}=\arg\mathrm{Topk}(\mathbf{A}),p_{i}=\left\lceil\frac{T}{f_{i}}\right\rceil,i\in\{1,\cdots,k\}. A=Avg(Amp(FFT(XID​))),{f1​,⋯,fk​}=argTopk(A),pi​=⌈fi​T​⌉,i∈{1,⋯,k}.
这里，$\mathrm{FFT}(\cdot )$和$\mathrm{Amp}(\cdot )$表示FFT和幅度值的计算。 $\text{A}\in {\mathbb{R}}^T$表示每个频率的计算振幅，该振幅从C维用AVG(·)平均。 注意，第j个值${\mathbf{A}}_j$表示频率j周期基函数的强度，对应于周期长度$\lceil \frac{T}{j}\rceil$。 考虑到频域的稀疏性和避免无意义的高频带来的噪声（Chatfield,1981；Zhou et al.，2022)，我们只选取顶部的k个振幅值，以非归一化振幅 { A f 1 , ⋯   , A f k } \{\mathbf{A}_{f_{1}},\cdots,\mathbf{A}_{f_{k}}\} {Af1​​,⋯,Afk​​}得到最有意义的频率 { f 1 , ⋯   , f k } \{f_{1},\cdots,f_{k}\} {f1​,⋯,fk​}，其中k为超参数。 这些选择的频率也对应于k个周期长度 { p 1 , ⋯   , p k } \{p_{1},\cdots,p_{k}\} {p1​,⋯,pk​}。 由于频域的共轭性，我们只考虑 { 1 , ⋯   , [ T 2 ] } \{1,\cdots,[\frac{T}{2}]\} {1,⋯,[2T​]}内的频率。 我们将等式1总结如下：
A , { f 1 , ⋯   , f k } , { p 1 , ⋯   , p k } = P e r i o d ( X 1 D ) . \mathbf{A},\{f_{1},\cdots,f_{k}\},\{p_{1},\cdots,p_{k}\}=\mathrm{Period}(\mathbf{X}_{1\mathrm{D}}). A,{f1​,⋯,fk​},{p1​,⋯,pk​}=Period(X1D​).
根据所选择的频率 { f 1 , ⋯   , f k } \{f_{1},\cdots,f_{k}\} {f1​,⋯,fk​}和相应的周期长度 { p 1 , ⋯   , p k } \{p_{1},\cdots,p_{k}\} {p1​,⋯,pk​},我们可以通过以下方程将一维时间序列${\mathbf{X}}_{\mathrm{lD}}\in {\mathbb{R}}^{T\times \bar{C}}$重塑为多个二维张量：
X 2 D i = R e s h a p e p i , f i ( P a d d i n g ( X l D ) ) , i ∈ { 1 , ⋯   , k } , \mathbf{X}_{2\mathbf{D}}^{i}=\mathrm{Reshape}_{p_{i},f_{i}}(\mathrm{Padding}(\mathbf{X}_{\mathrm{lD}})),i\in\{1,\cdots,k\}, X2Di​=Reshapepi​,fi​​(Padding(XlD​)),i∈{1,⋯,k},
其中$Padding(\cdot )$是将时间序列沿时间维扩展零，使其与${\mathrm{Reshape}}_{p_i,f_i}(\cdot )$兼容，其中$p_i$和$f_i$分别表示变换后的二维张量的行数和列数。 注意，${\mathbf{X}}_{2\mathrm{D}}^i\in {\mathbb{R}}^{p_i\times f_i\times C}$表示基于frequency-fi的第i次整形时间序列，其列和行分别表示相应周期长度pi下的周期内变化和周期间变化。 最后，如图2所示，基于所选择的频率和估计的周期，我们得到一组2D张量 { X 2 D 1 , ⋯   , X 2 D k } \{\mathbf{X}_{2\mathrm{D}}^{1},\cdots,\mathbf{X}_{2\mathrm{D}}^{k}\} {X2D1​,⋯,X2Dk​}，它表示由不同周期导出的k个不同的时间2D变化。

值得注意的是，这种变换给变换后的二维张量带来了两种类型的局部，即相邻时间点之间的局部（列，周期内变化）和相邻周期之间的局部（行，周期间变化）。 因此，时间的二维变化可以很容易地被二维核处理。

3.2 Times Block

如图3所示，我们以残差方式组织时间块（He et al.，2016)。 具体而言，对于长度为$t1D$的输入时间序列${\mathbf{X}}_{1D}\in {\mathbb{R}}^{T\times C}$，我们首先通过嵌入层${\mathbf{X}}_{\mathrm{lD}}^0=\mathrm{Embed}({\mathbf{X}}_{\mathrm{lD}})$将原始输入投影到深度特征${\mathbf{X}}_{\mathrm{lD}}^0\in {\mathbb{R}}^{T\times d_{\mathrm{model}}}$中。 对于TimesNet的第L层，输入为${\mathbf{X}}_{\mathrm{lD}}^{l-1}\in {\mathbb{R}}^{T\times d_{\mathrm{model}}}$，过程可以形式化为：
$${\mathbf{X}}_{\mathrm{lD}}^l=\mathrm{TimesBlock}\left({\mathbf{X}}_{\mathrm{lD}}^{l-1}\right)+{\mathbf{X}}_{\mathrm{lD}}^{l-1}.$$
如图3所示，对于第$l$个时间块，整个过程包括两个连续的部分：捕获时间的2D变化和自适应地聚合来自不同时期的表示。

捕捉时间二维变化 与公式 1 类似，我们可以通过$\mathrm{Period}(\cdot )$来估计深度特征${\mathbf{X}}_{\mathrm{lD}}^{l-1}$的周期长度。根据估计的周期长度，我们可以转换一维时间序列 转换到二维空间，得到一组二维张量，我们可以通过参数效率高的截取块方便地从中获取信息表示。具体过程如下
A l − 1 , { f 1 , ⋯   , f k } , { p 1 , ⋯   , p k } = P e r i o d ( X l D l − 1 ) , x 2 D l , i = R e s h a p e p i , f i ( P a d d i n g ( X l D l − 1 ) ) , i ∈ { 1 , ⋯   , k } x ^ 2 D l , i = I n c e p t i o n ( X 2 D l , i ) , i ∈ { 1 , ⋯   , k } X ^ 1 D l , i = T r u n c ( R e s h a p e 1 , ( p i × f i ) ( X ^ 2 D l , i ) ) , i ∈ { 1 , ⋯   , k } , \begin{aligned} \mathbf{A}^{l-1},\{f_{1},\cdots,f_{k}\},\{p_{1},\cdots,p_{k}\}& =\mathrm{Period}\left(\mathbf{X}_{\mathrm{lD}}^{l-1}\right), \\ \mathbf{x}_{2\mathrm{D}}^{l,i}& =\mathrm{Reshape}_{p_{i},f_{i}}\left(\mathrm{Padding}(\mathbf{X}_{\mathrm{lD}}^{l-1})\right),i\in\{1,\cdots,k\} \\ \hat{\mathbf{x}}_{2\mathrm{D}}^{l,i}& =\mathrm{Inception}\left(\mathbf{X}_{2\mathrm{D}}^{l,i}\right),i\in\{1,\cdots,k\} \\ {\hat{\mathbf{X}}}_{\mathrm{1D}}^{l,i}& =\mathrm{Trunc}\left(\mathrm{Reshape}_{1,(p_{i}\times f_{i})}\left(\widehat{\mathbf{X}}_{2\mathrm{D}}^{l,i}\right)\right),i\in\{1,\cdots,k\}, \end{aligned} Al−1,{f1​,⋯,fk​},{p1​,⋯,pk​}x2Dl,i​x^2Dl,i​X^1Dl,i​​=Period(XlDl−1​),=Reshapepi​,fi​​(Padding(XlDl−1​)),i∈{1,⋯,k}=Inception(X2Dl,i​),i∈{1,⋯,k}=Trunc(Reshape1,(pi​×fi​)​(X 2Dl,i​)),i∈{1,⋯,k},​

其中，${\mathbf{X}}_{2\mathrm{D}}^{l,i}\in {\mathbb{R}}^{p_i}\times f_i\times d_{\mathrm{model}}$是第i次变换的二维张量。 转换后的二维张量由参数有效的inception块（Szegedy et al.，2015)作为inception(·)进行处理，该块涉及多尺度的二维核，是公认的视觉主干之一。 然后将学习到的二维表示${\hat{\mathbf{X}}}_{2\mathrm{D}}^{l,i}$变换回一维空间${\hat{\mathbf{X}}}_{\mathrm{lD}}^{l,i}\in {\mathbb{R}}^{T\times d_{\mathrm{model}}}$进行聚合，其中用Trunc(·)将长度为$(p_i\times f_i)$的填充级数截断为原始长度T。

需要注意的是，受益于一维时间序列的转换，起始块中的二维核可以同时聚合多尺度的期内变化（列）和期间变化（行），覆盖相邻的时间点和相邻的时期。此外，为了提高参数效率，我们对不同的重塑二维张量 { X 2 D l , 1 , ⋯   , X 2 D l , k } \{\mathbf{X}_{2\mathrm{D}}^{l,1},\cdots,\mathbf{X}_{2\mathrm{D}}^{l,k}\} {X2Dl,1​,⋯,X2Dl,k​}采用共享起始块，这可以使模型大小不受超参数 k 选择的影响。

自适应聚合最后，我们需要融合k个不同的1D表示 { X ^ l D l , 1 , ⋯   , X ^ l D l , k } \{\widehat{\mathbf{X}}_{\mathrm{lD}}^{l,1},\cdots,\widehat{\mathbf{X}}_{\mathrm{lD}}^{l,k}\} {X lDl,1​,⋯,X lDl,k​}进行下一层。 受自相关（Wu et al.，2021)的启发，振幅A可以反映所选频率和周期的相对重要性，从而对应于每个转换后的2D张量的重要性。 因此，我们聚集了基于振幅的一维表示：
$$\begin{array}{c}{\hat{\mathbf{A}}}_{f_1}^{l-1},\cdots ,{\hat{\mathbf{A}}}_{f_k}^{l-1}=\mathrm{Softmax}\left({\mathbf{A}}_{f_1}^{l-1},\cdots ,{\mathbf{A}}_{f_k}^{l-1}\right)\\ {\mathbf{x}}_{\mathrm{lD}}^l=\sum _{i=1}^k{\hat{\mathbf{A}}}_{f_i}^{l-1}\times {\hat{\mathbf{X}}}_{\mathrm{lD}}^{l,i}.\end{array}$$
由于周期内和周期间的变化已经包含在多个高度结构化的二维张量中，TimesBlock可以同时完全捕捉多尺度的时间二维变化。 因此，TimesNet可以实现比直接从一维时间序列中学习更有效的表示方法。

由于一维时间序列向时间二维变化的转换，我们可以选择各种计算机视觉主干来代替表征学习的起始块，如广泛使用的ResNet（He et al.，2016)和ResNext（Xie et al.，2017)、先进的ConvNext（Liu et al.，2022b)和基于注意力的模型（Liu et al.，2021b)。 因此，我们的时间二维变化设计也将一维时间序列与蓬勃发展的二维视觉主干连接起来，使时间序列分析利用计算机视觉社区的发展。 一般来说，更强大的2D表示学习骨干将带来更好的性能。 考虑到性能和效率（图4右），我们基于参数有效的inception块进行主要实验，如公式5所示。

4. 实验