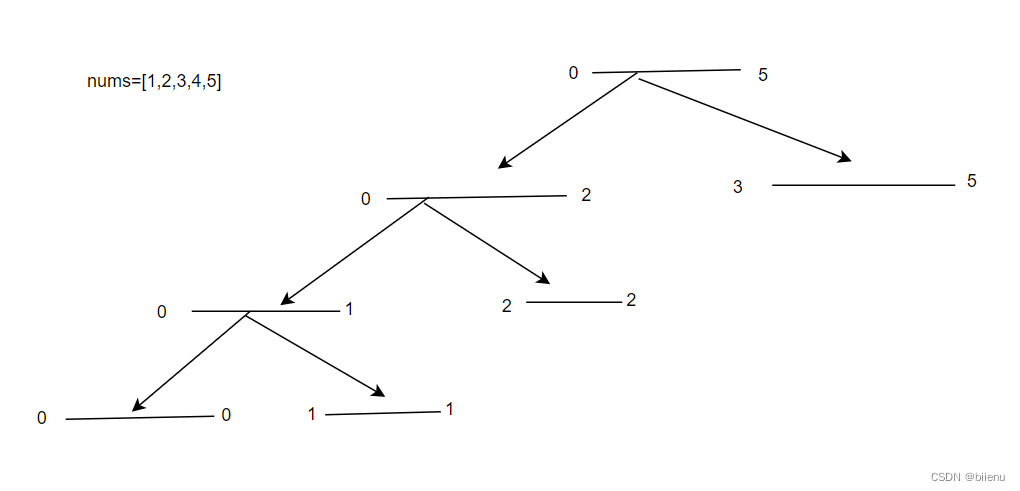
学计算机的对这道题肯定不陌生，我记得是学C语言的时候学递归的时候有这道题，于是我就世界用递归写了如下代码：

class Solution {
    public int fib(int n) {
        if(n==1) return 1;
        if(n==0) return 0;
        return (fib(n-1) + fib(n-2)) % 1000000007;
    }
}

到n=44就算不出了，超时了。就看了一下题解，题解用的是动态规划的方法：

class Solution {
    public int fib(int n) {
        if(n<2){
            return n;
        }
        int p=0,q=1;int r =0;
        for(int i =2;i<=n;i++){
            r = (p+q) % 1000000007;
            p = q;
            q = r;       
        }
        return r;
    }
}

n小于2的话返回自己，然后定义p为n的前两个数，q为n的前一个数，然后r是第n个数的值，所以r就等于p+q，然后把q给p，r给q，最后返回r就可以了。

题解还给出了一种矩阵幂的方法：

 最后只需要求M的n次方就行。

class Solution {
    static final int MOD = 1000000007;

    public int fib(int n) {
        if (n < 2) {
            return n;
        }
        int[][] q = {{1, 1}, {1, 0}};
        int[][] res = pow(q, n - 1);
        return res[0][0];
    }

    public int[][] pow(int[][] a, int n) {
        int[][] ret = {{1, 0}, {0, 1}};
        while (n > 0) {
            if ((n & 1) == 1) {
                ret = multiply(ret, a);
            }
            n >>= 1;
            a = multiply(a, a);
        }
        return ret;
    }

    public int[][] multiply(int[][] a, int[][] b) {
        int[][] c = new int[2][2];
        for (int i = 0; i < 2; i++) {
            for (int j = 0; j < 2; j++) {
                c[i][j] = (int) (((long) a[i][0] * b[0][j] + (long) a[i][1] * b[1][j]) % MOD);
            }
        }
        return c;
    }
}

定义了一个矩阵乘矩阵的multiply方法，求矩阵的n次方的pow方法，通过这两个方法可以求出M的n次方。