leetcode原题链接

题目描述：

给你一个整数数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。

返回 滑动窗口中的最大值 。

示例1:

输入：nums = [1,3,-1,-3,5,3,6,7], k = 3
输出：[3,3,5,5,6,7]
解释：
滑动窗口的位置                最大值
---------------               -----
[1  3  -1] -3  5  3  6  7       3
 1 [3  -1  -3] 5  3  6  7       3
 1  3 [-1  -3  5] 3  6  7       5
 1  3  -1 [-3  5  3] 6  7       5
 1  3  -1  -3 [5  3  6] 7       6
 1  3  -1  -3  5 [3  6  7]      7

示例2：

输入：nums = [1,3,0,2,4]
输出：0
解释：
nums 无论怎么变化总是有 3 分。
所以我们将选择最小的 k，即 0。

提示：

• 1 <= nums.length <= 105
• -104 <= nums[i] <= 104
• 1 <= k <= nums.length

解题思路：

方法一：单调队列

单调队列：队列中的元素是单调递增或单调递减的队列就是单调队列。

---

1. 维护队列中的元素递增：

对于这道题需要维护一个单调递增的队列。

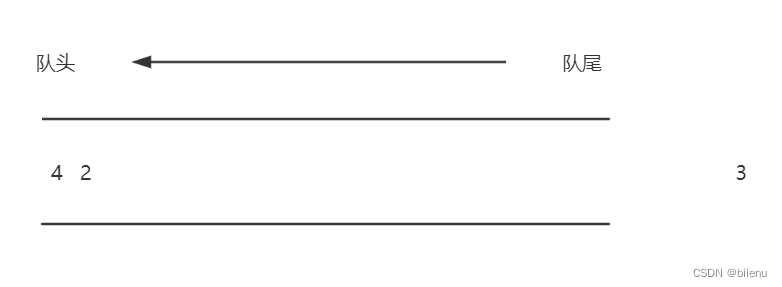
由队尾到队头 元素是单调递增的。如果要入队元素大于队尾元素，则队尾元素出队，这是个循环操作，如下：

while(deque.peekLast() < newElement){
	deque.pollLast();
}
deque.push(newElement); // 新元素入队

---

2. 如何保证队列中的元素是窗口内的，因为窗口一直在向右移动？

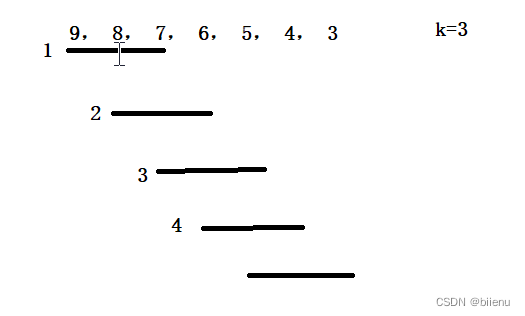
初始时，窗口为1，队列中元素为9, 8, 7。窗口向右移动时(窗口2)发现9已不是窗口中的元素，但9依然在队列中，且9为队列的队头元素，需要将9从队列的队头弹出。所以需要进行如下判断:

if(deque.peekFirst() == v){ // v为上一个窗口最左边的值。
    deque.poolFirst();
}

整体代码如下：

public int[] maxSlidingWindow(int[] nums, int k) {
    int n = nums.length;
    int[] ans = new int[n - k + 1];
    Deque<Integer> deque = new LinkedList<>();
    int idx = 0;
    for(int i = 0; i < nums.length; i++){

        // 保证队列中的元素是窗口内的
        if(!deque.isEmpty() && i - k>= 0 && nums[i - k] == deque.peekFirst()){
            deque.pollFirst();
        }
        // 维护队列中的元素是递增的
        while (!deque.isEmpty() && nums[i] > deque.peekLast()){
            deque.pollLast();
        }
        deque.addLast(nums[i]);
        if(i>= k - 1){
            ans[idx++] = deque.peekFirst();
        }
    }
    return ans;
}

---

方法二：线段树

百度百科：线段树

---

线段树中的每个节点存储的是这个区间的最大值。

整体代码如下：

public int[] maxSlidingWindow(int[] nums, int k) {
    int len = nums.length;
    int[] ans = new int[len - k + 1];
    this.tr = new Node[len * 4+1];
    build(1,1,len);
    for(int i = 0; i<len;i++){
        update(1,i+1,nums[i]);
    }
    for(int i = 0; i< len -k+1;i++){
        ans[i] = query(1,i+1,i+k);
    }
    return ans;
}

class Node {
    int l, r, v;
    Node(int l, int r) {
        this.l = l;
        this.r = r;
        v = Integer.MIN_VALUE;
    }
}

Node[] tr;

void pushup(int u) {
    tr[u].v = Math.max(tr[u << 1].v, tr[u << 1 | 1].v);
}

void build(int u, int l, int r) {
    tr[u] = new Node(l, r);
    if (l != r) {
        int mid = tr[u].l+tr[u].r >> 1;
        build(u << 1, l, mid);
        build(u << 1 | 1, mid + 1, r);
    }
}

void update(int u, int x, int v){
    if(x== tr[u].l&&tr[u].r==x){
        tr[u].v = Math.max(tr[u].v, v);
    } else{
        int mid = tr[u].l+tr[u].r>>1;
        if(x<=mid){
            update(u<<1,x,v);
        } else{
            update(u<<1|1,x,v);
        }
        pushup(u);
    }
}
int query(int u, int l, int r){
    if(l<= tr[u].l&&tr[u].r<=r){
        return tr[u].v;
    } else{
        int mid = tr[u].l+tr[u].r>>1;
        int ans = Integer.MIN_VALUE;
        if(l<=mid){
            ans =query(u<<1,l,r);
        } 
        if(r>mid){
            ans = Math.max(query(u<<1|1,l,r),ans);
        }
        return ans;
    }
}