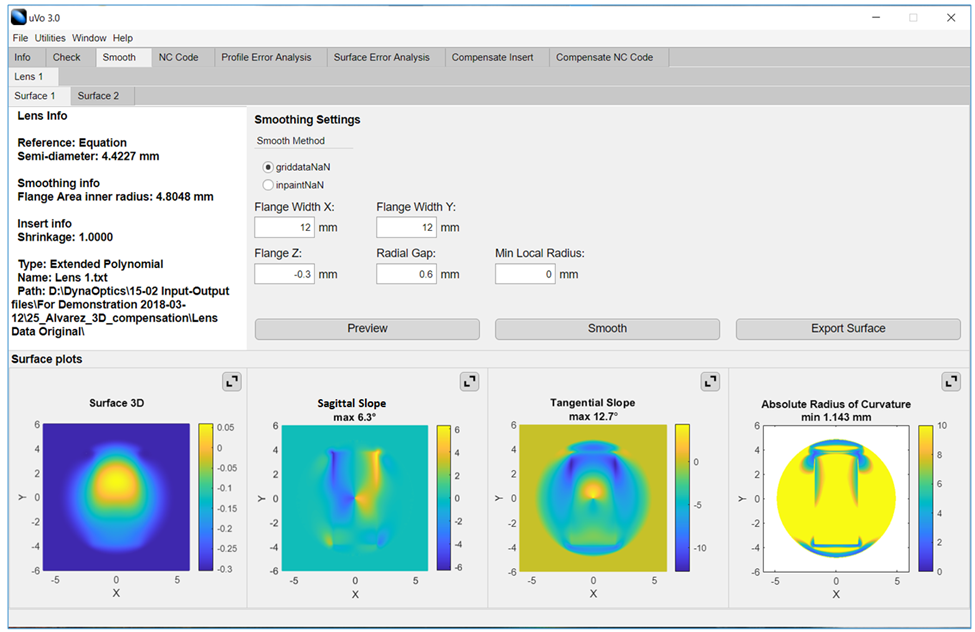
给定一个整型数组arr,代表数值不同的纸牌排成一条线
玩家A和玩家B依次拿走每张纸牌
规定玩家A先拿,玩家B后拿
但是每个玩家每次只能拿走最左或最右的纸牌
玩家A和玩家B都绝顶聪明
请返回最后获胜者的分数
方法一:暴力解法
自然智慧。
package algorithmbasic.class19;
public class CardsInLine {
public static int win2(int[] arr) {
if (arr == null || arr.length < 2) {
return -1;
}
int fresult = f2(arr, 0, arr.length - 1);
int gresult = g2(arr, 0, arr.length - 1);
return Math.max(fresult, gresult);
}
//作为先手函数,要在arr[L......R]范围上返回最好的成绩。
public static int f2(int[] arr, int L, int R) {
//如果现在只剩下一张纸牌了,作为先手直接拿走即可。
if (L == R) {
return arr[L];
}
//不止一张纸牌
//如果我将最左侧的纸牌拿走,那接下来后手会怎么拿呢?然后就把自己当作后手来分析一下后手会如何做。
int p1 = arr[L] + g2(arr, L + 1, R);
//如果我将最右侧的纸牌拿走,那接下来后手会怎么拿呢?然后就把自己当作后手来分析一下后手会如何做。
int p2 = arr[R] + g2(arr, L, R - 1);
return Math.max(p1, p2);
}
private static int g2(int[] arr, int L, int R) {
if (L == R) {
return 0;
}
// 后手拿走最左侧的数,然后判断先手会在剩下的【L + 1, R】范围上的最优解。
int p1 = f2(arr, L + 1, R);
// 后手拿走最右侧的数,然后判断先手会在剩下的【L , R - 1】范围上的最优解。
int p2 = f2(arr, L, R - 1);
// p1 -> 先手在的【L + 1, R】范围上的最优解。
// p2 -> 先手在的【L, R - 1】范围上的最优解。
// 因为先手与后手都绝顶的聪明,所以最优解一定会被先手拿走。后手只能返回两者中最小的结果。
//后手只能返回一个最小的,因为大的那个已经被先手拿走了。
return Math.min(p1, p2);
}
// 给定数组arr之后,绝顶聪明的先手与后手的结果其实早已决定无力回天。 ----> 命运的安排
// 于此同时主动权一直在先手这方。
}
方法二:记忆化搜索优化
暴力函数
public static int win1(int[] arr) {
int f = f1(arr, 0, arr.length - 1);
int l = g1(arr, 0, arr.length - 1);
return Math.max(f, l);
}
//返回先手在arr[L......R]范围上的最优分数。
public static int f1(int[] arr, int L, int R) {
if (L == R) {
return arr[L];
}
int p1 = arr[L] + g1(arr, L + 1, R);
int p2 = arr[R] + g1(arr, L, R - 1);
return Math.max(p1, p2);
}
private static int g1(int[] arr, int L, int R) {
if (L == R) {
return 0;
}
int p1 = f1(arr, L + 1, R);
int p2 = f1(arr, L, R - 1);
return Math.min(p1, p2);
}
1:分析原函数
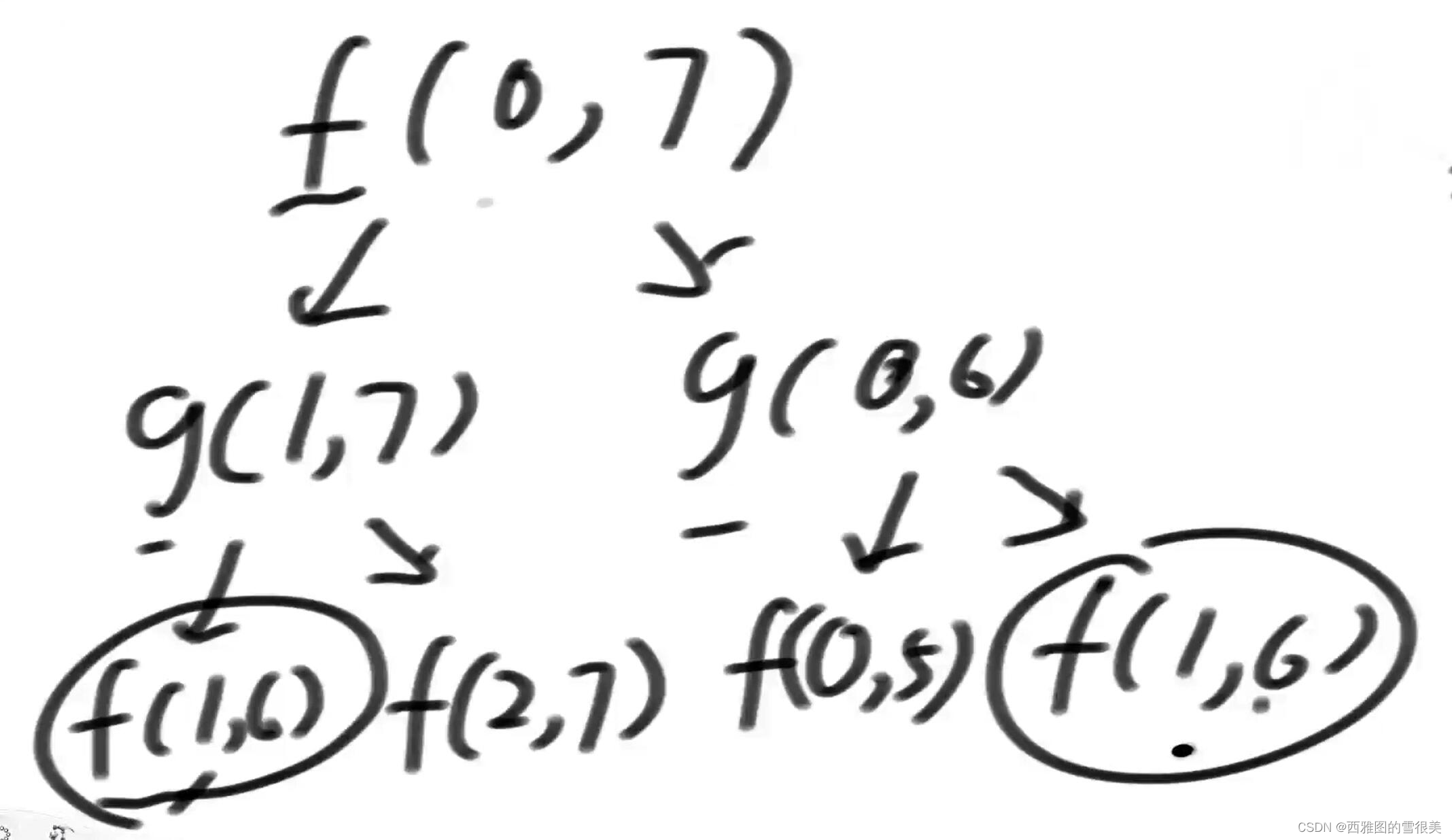
发现加入缓存是合理的,因为真的出现重复计算了。
2:确定建立几张表以及表的范围
因为g方法与f方法都可能存在重复,所以建立两张表,表的范围是 [N] [N]
3:将表加入到原函数中。
// 方法二:记忆化搜索。
private static int win2(int[] arr) {
int N = arr.length;
int[][] fmap = new int[N][N];
int[][] gmap = new int[N][N];
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
fmap[i][j] = -1;
gmap[i][j] = -1;
}
}
int f = f2(arr, 0, arr.length - 1, fmap, gmap);
int l = g2(arr, 0, arr.length - 1, fmap, gmap);
return Math.max(f, l);
}
public static int f2(int[] arr, int L, int R, int[][] fmap, int[][] gmap) {
if (fmap[L][R] != -1) {
return fmap[L][R];
}
int ans = -1;
if (L == R) {
ans = arr[L];
} else {
int p1 = arr[L] + g2(arr, L + 1, R, fmap, gmap);
int p2 = arr[R] + g2(arr, L, R - 1, fmap, gmap);
ans = Math.max(p1, p2);
}
fmap[L][R] = ans;
return ans;
}
private static int g2(int[] arr, int L, int R, int[][] fmap, int[][] gmap) {
if (gmap[L][R] != -1) {
return gmap[L][R];
}
int ans = -1;
if (L == R) {
ans = 0;
} else {
int p1 = f2(arr, L + 1, R, fmap, gmap);
int p2 = f2(arr, L, R - 1, fmap, gmap);
ans = Math.min(p1, p2);
}
gmap[L][R] = ans;
return ans;
}
方法三:依赖版本迭代实现
1:分析依赖关系,确定表的大小
**分析依赖关系:**f 函数依赖g 函数,g 函数还会依赖 f 函数。
–> f 函数与g 函数中可能都存在重复值 --> 建两张表
确定表的大小关系:
public static int f1(int[] arr, int L, int R) {。。。。}
private static int g1(int[] arr, int L, int R) {。。。。}
L的范围与R的范围不会超过数组的长度。
所以两张表的大小可以都是arr[arr.length] [arr.length]
2:根据原函数从上到下开始逐一分析
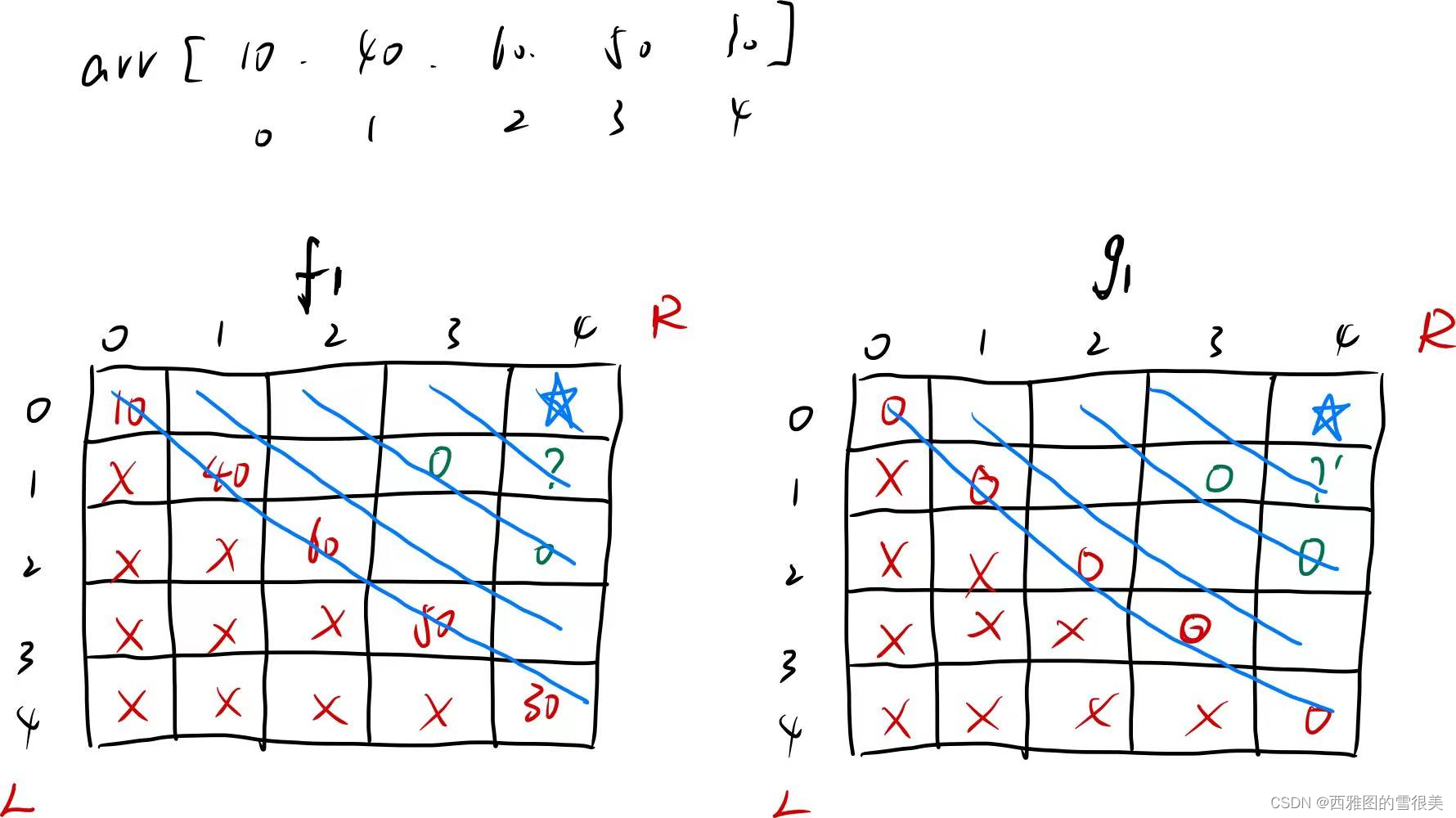
首先分析一下结果想要什么
public static int win1(int[] arr) {
int f = f1(arr, 0, arr.length - 1);
int l = g1(arr, 0, arr.length - 1);
return Math.max(f, l);
}
发现结果想要的是f1图中的 (0, n-1 )位置。
以及g1图中的 (0, n-1 )位置。
分析f1方法
public static int f1(int[] arr, int L, int R) {
if (L == R) {
return arr[L];
}
int p1 = arr[L] + g1(arr, L + 1, R);
int p2 = arr[R] + g1(arr, L, R - 1);
return Math.max(p1, p2);
}
当L == R的时候,返回的是arr [L] - -> 直接在表中写出来。
当L != R时,即L < R时,会依赖 g1 方法。会依赖方法的那个位置呢?依赖的位置是:在f1图中的位置对应到g1图中的位置,
依赖的是在g1图中位置的左侧与下侧位置。与此同时,g1方法的依赖关系与f1一样。
3:根据原函数开始填表
原始函数
public static int win1(int[] arr) {
int f = f1(arr, 0, arr.length - 1);
int l = g1(arr, 0, arr.length - 1);
return Math.max(f, l);
}
//返回先手在arr[L......R]范围上的最优分数。
public static int f1(int[] arr, int L, int R) {
if (L == R) {
return arr[L];
}
int p1 = arr[L] + g1(arr, L + 1, R);
int p2 = arr[R] + g1(arr, L, R - 1);
return Math.max(p1, p2);
}
private static int g1(int[] arr, int L, int R) {
if (L == R) {
return 0;
}
int p1 = f1(arr, L + 1, R);
int p2 = f1(arr, L, R - 1);
return Math.min(p1, p2);
}
填表的最终结果如下:
private static int win3(int[] arr) {
int N = arr.length;
int[][] fmap = new int[N][N];
int[][] gmap = new int[N][N];
//根据f1中if (L == R) {return arr[L]; } 以及g1中的第一句话。
for (int col = 0; col < N; col++) {
fmap[col][col] = arr[col];
gmap[col][col] = 0;
}
for (int start = 1; start < N; start++) {
//斜着填
int row = 0;
int col = start;
while(col < N) {
fmap[row][col] = Math.max(arr[row] + gmap[row][col - 1],
arr[row] + gmap[row + 1][col]);
gmap[row][col] = Math.min(fmap[row][col - 1], fmap[row + 1][col]);
row++;
col++;
}
}
return Math.max(fmap[0][N - 1], gmap[0][N - 1]);
}