【数据结构】实验五：栈

news2024/11/18 23:51:43

实验五  栈

一、实验目的与要求

1）熟悉栈的类型定义和基本操作；

2）灵活应用栈解决具体应用问题。

二、实验内容

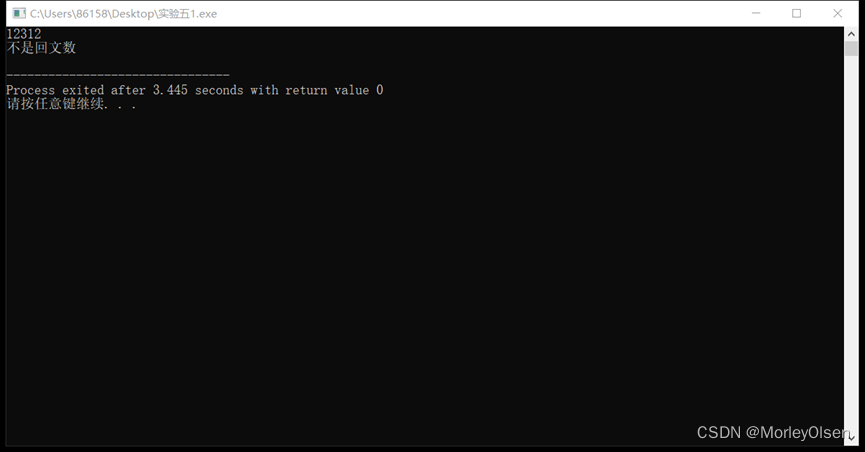
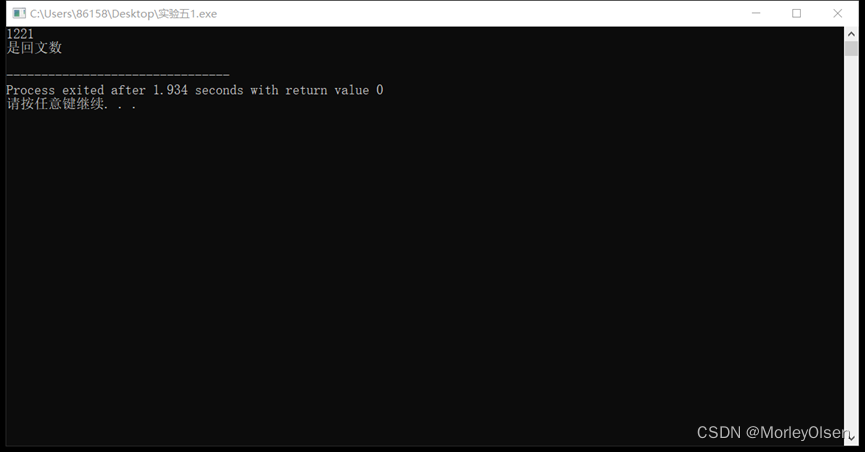
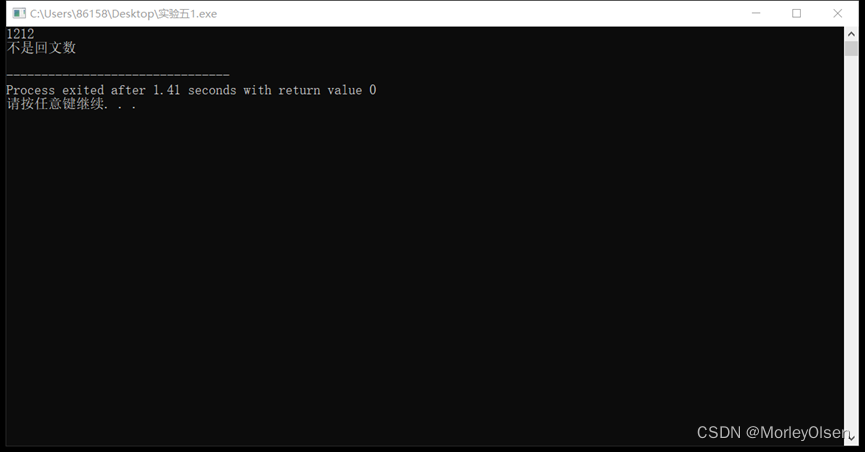
1、判断回文数，回文是指正读反读均相同的字符序列，如“1221”和“12321”均是回文，但“1234”不是回文。请写一个算法判定给定的字符向量是否为回文。(提示：将一半字符入栈)

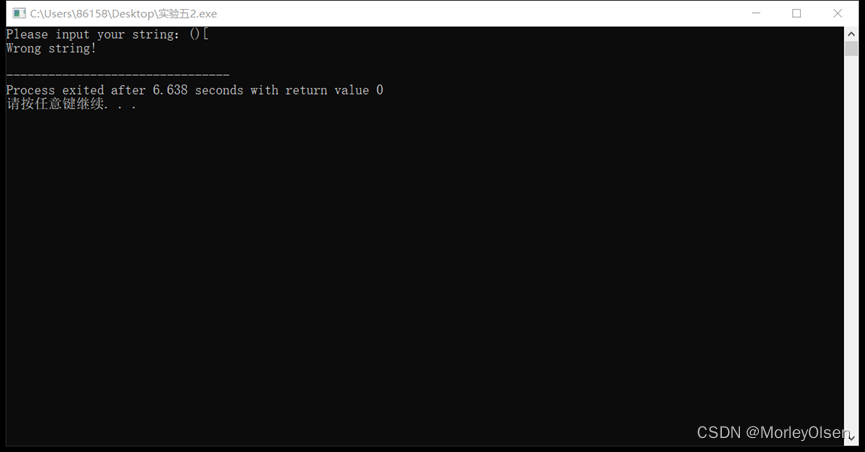
2、给定一个只包括 '('，')'，'{'，'}'，'['，']' 的字符串s ，判断字符串是否有效。有效字符串需满足：

左括号必须用相同类型的右括号闭合。

左括号必须以正确的顺序闭合。

示列："()"和"()[]{}"都是合法的括号序列，但"( ]"和"( [ )]"不合法。

3、在某程序中，有两个栈共享一个一维数组空间SPACE[N]，SPACE[0]、SPACE[N-1] 分别是两个栈的栈底。(扩展选作)

  （1）对栈1、栈2，试分别写出（元素x）入栈的主要语句和出栈的主要语句。

  （2）对栈1、栈2，试分别写出栈满、栈空的条件。

三、实验结果

1）请将调试通过的源代码粘贴在下面。（代码注意书写规范、主要模块要有功能注释）

实验1代码：

#include <iostream>
#include <cstring>
using namespace std;
typedef struct{
	char data[1000];
	int top;
}Stack;

//初始化栈 
void Init_stack(Stack *s){
	s->top=-1;
}

//元素入栈 
void Push_stack(Stack *s,char x){
	s->top=s->top+1;
	s->data[s->top]=x;
}

//元素出栈 
void Pop_stack(Stack *s,char *x){
	*x=s->data[s->top];
	s->top=s->top-1;
}
 
int main(){
	char data[1000],x;
	int i;
	Stack s;
	
	//初始化测试栈 
	Init_stack(&s);
	cin>>data;
	
	//输入的字符串长度 
	int len=strlen(data);
	
	//输入的字符串入栈 
	for(i=0;i<len;i++){
		Push_stack(&s,data[i]);
	}
	
	//首尾对比，判断回文数 
	for(i=0;i<len;i++){
		Pop_stack(&s,&x);
		if(data[i]!=x){
			cout<<"不是回文数"<<endl;
			return 0;
		}
	}
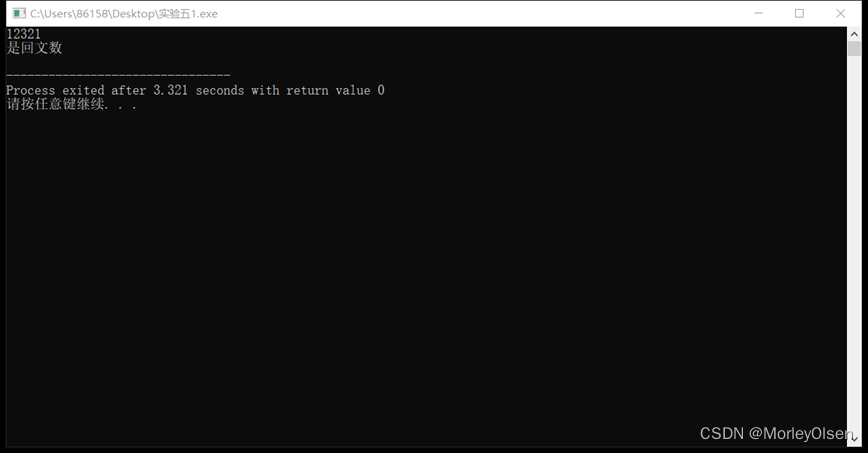
	cout<<"是回文数"<<endl;
	return 0;
}

实验1结果展示：

 

 

 

 实验2代码：

#include <iostream>
#include <cstring>
using namespace std;

typedef struct{
	char data[1000];//元素 
	int top;//顶指针 
}Stack;

//初始化栈 
void Init_stack(Stack *s){
	s->top=-1;
}

//元素入栈 
void Push_stack(Stack *s,char *x){
	s->top=s->top+1;
	s->data[s->top]=*x;
}

//元素出栈 
void Pop_stack(Stack *s,char *x){
	*x=s->data[s->top];
	s->top=s->top-1;
}

int main(){
	char str[1000];
	Stack s;
	Init_stack(&s);
	cout<<"Please input your string：";
	cin>>str;
	int len=strlen(str),i=0;//len为str的长度 
	//cout<<len;
	
	//如果长度为奇数，一定缺少括号 
	if(len%2!=0){
		cout<<"Wrong string!"<<endl;
		return 0;
	}
	
	//长度为偶数，分类讨论 
	for(i=0;i<len;i++){
		//[]情况 
		if(str[i]=='['){
			Push_stack(&s,&str[i]);
			if(str[i+1]==']'){
				Pop_stack(&s,&str[i]);
				continue;
			}
			else{
				cout<<"Wrong string!"<<endl;
				return 0;
			}
		}
		//()情况 
		if(str[i]=='('){
			Push_stack(&s,&str[i]);
			if(str[i+1]==')'){
				Pop_stack(&s,&str[i]);
				continue;
			}
			else{
				cout<<"Wrong string!"<<endl;
				return 0;
			}
		}
		//{}情况 
		if(str[i]=='{'){
			Push_stack(&s,&str[i]);
			if(str[i+1]=='}'){
				Pop_stack(&s,&str[i]);
				continue;
			}
			else{
				cout<<"Wrong string!"<<endl;
				return 0;
			}
		}
	}
	cout<<"Right string!"<<endl; 
	return 0;
}

实验2结果展示：

 

 

 

 

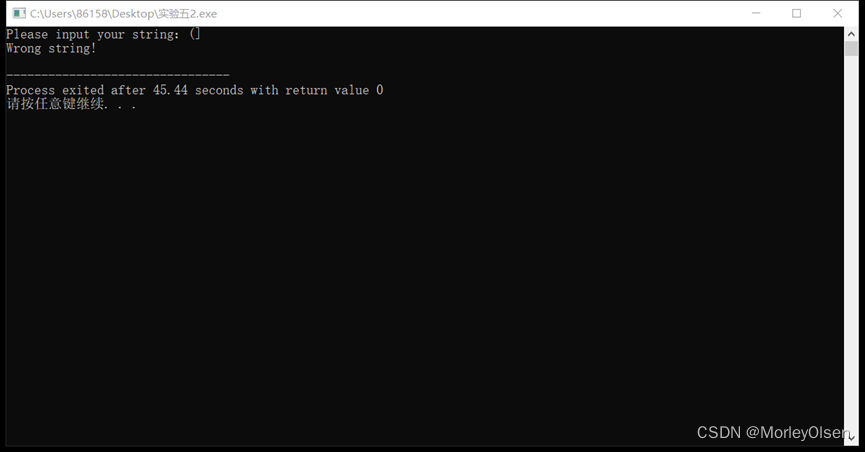
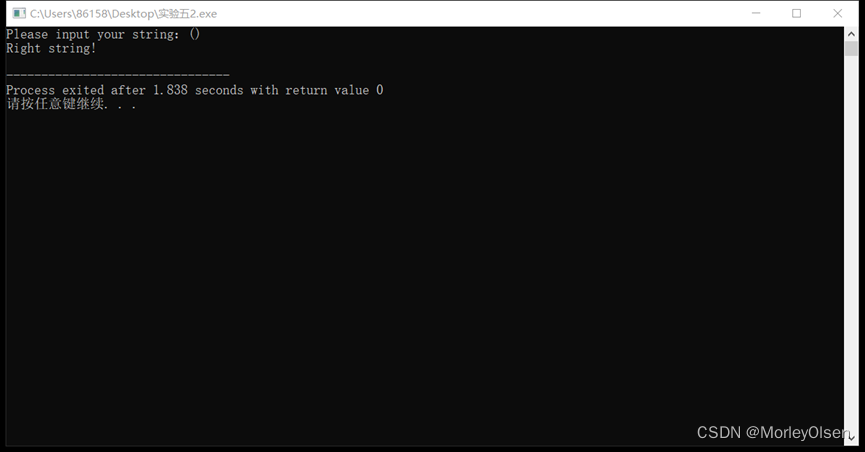
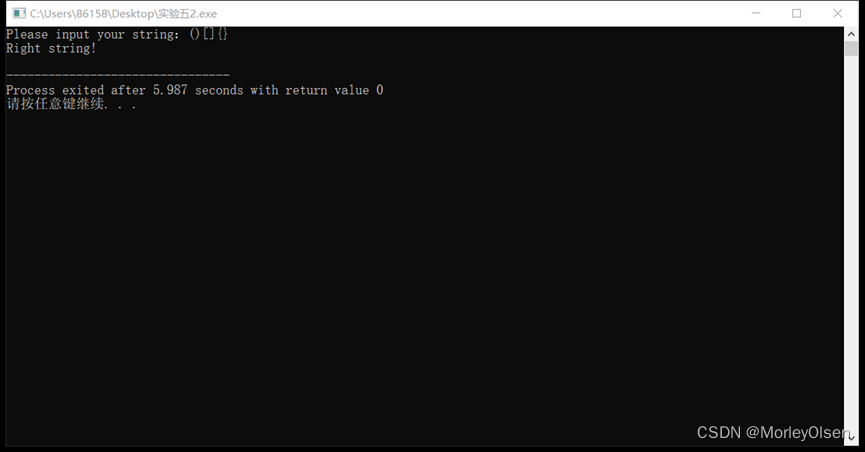
 实验3代码：

#include <cstdio>
#define MaxSize 10 //栈的容量 
#define ElemType int
#include <iostream>
using namespace std;			

typedef struct {
	ElemType data[MaxSize];		
	int top1;//1号栈栈顶指针
	int top2;//2号栈栈顶指针
}ShStack;

//初始化共享栈
void InitShStack(ShStack& S) {
	S.top1 = -1;//初始化1号栈栈顶指针
	S.top2 = MaxSize;//初始化2号栈栈顶指针
}

//1号栈判空
bool Stack1Empty(ShStack S) {
	return (S.top1 == -1);
}

//2号栈判空
bool Stack2Empty(ShStack S) {
	return (S.top2 == MaxSize);
}

//1号栈入栈操作：新元素入栈(先存再加)
bool Push1(ShStack& S, ElemType x) {
	if (S.top1+1 == S.top2){
		return false;//栈满，报错
	}
	S.data[++S.top1] = x;
	return true;
}

//2号栈入栈操作：新元素入栈(先存再加)
bool Push2(ShStack& S, ElemType x) {
	if (S.top1+1 == S.top2){
		return false;//栈满，报错
	}
	S.data[--S.top2] = x;
	return true;
}

//1号栈出栈操作：栈顶元素出栈
bool Pop1(ShStack& S, ElemType& x) {
	if (S.top1 == -1){
		return false;//1号栈栈空，报错
	}
	x = S.data[S.top1--];	
	return true;
}

//2号栈出栈操作：栈顶元素出栈
bool Pop2(ShStack& S, ElemType& x) {
	if (S.top2 == MaxSize){
		return false;//2号栈栈空，报错
	}
	x = S.data[S.top2++];
	return true;
}

//1号栈读取栈顶元素操作
bool GetTop1(ShStack S, ElemType& x) {
	if (S.top1 == -1){
		return false;//1号栈栈空，报错
	}
	x = S.data[S.top1];
	return true;
}

//2号栈读取栈顶元素操作
bool GetTop2(ShStack S, ElemType& x) {
	if (S.top2 == MaxSize){
		return false;//2号栈栈空，报错
	}
	x = S.data[S.top2];
	return true;
}

int main() {
	//声明一个共享栈
	ShStack S;		

	//初始化共享栈
	InitShStack(S);

	//1号栈-判空
	if(Stack1Empty(S)){
		printf("当前1号栈空！\n");
	}
	else{
		printf("当前1号栈非空！\n");
	}
	
	//1号栈-入栈操作
	ElemType e1;
	printf("请输入1号栈入栈元素的值：");
	scanf("%d", &e1);
	if(Push1(S, e1)){
		printf("1号栈新元素入栈成功！\n");
	}
	else{
		printf("共享栈已满,1号栈新元素入栈失败！\n");
	}

	//1号栈-读取栈顶元素
	ElemType e2 = -1;
	if(GetTop1(S, e2)){
		printf("1号栈读取栈顶元素成功，当前栈顶元素值为：%d\n", e2);
	}
	else{
		printf("1号栈已空，读取栈顶元素失败！\n");
	}

	//1号栈-出栈操作
	ElemType e3 = -1;
	if(Pop1(S, e3)){
		printf("1号栈栈顶元素出栈成功，出栈元素值为：%d\n", e3);
	}
	else{
		printf("1号栈已空，栈顶元素出栈失败！\n");
	}

	//1号栈-读取栈顶元素
	ElemType e4 = -1;
	if (GetTop1(S, e4))
		printf("1号栈读取栈顶元素成功，当前栈顶元素值为：%d\n", e4);
	else
		printf("1号栈已空，读取栈顶元素失败！\n");
		
	cout<<endl;

	//2号栈-判空
	if (Stack2Empty(S)){
		printf("当前2号栈空！\n");
	}
	else{
		printf("当前2号栈非空！\n");
	}

	//2号栈-入栈操作
	ElemType e21;
	printf("请输入2号栈入栈元素的值：");
	scanf("%d", &e21);
	if (Push2(S, e21)){
		printf("2号栈新元素入栈成功！\n");
	}
	else{
		printf("共享栈已满,2号栈新元素入栈失败！\n");
	}

	//2号栈-读取栈顶元素
	ElemType e22 = -1;
	if (GetTop2(S, e22)){
		printf("2号栈读取栈顶元素成功，当前栈顶元素值为：%d\n", e22);
	}
	else{
		printf("2号栈已空，读取栈顶元素失败！\n");
	}
	
	//2号栈-出栈操作
	ElemType e23 = -1;
	if (Pop2(S, e23)){
		printf("2号栈栈顶元素出栈成功，出栈元素值为：%d\n", e23);
	}
	else{
		printf("2号栈已空，栈顶元素出栈失败！\n");
	}

	//2号栈-读取栈顶元素
	ElemType e24 = -1;
	if (GetTop2(S, e24)){
		printf("2号栈读取栈顶元素成功，当前栈顶元素值为：%d\n", e24);
	}
	else{
		printf("2号栈已空，读取栈顶元素失败！\n");
	}
		
	return 0;
}

实验3结果展示：

 

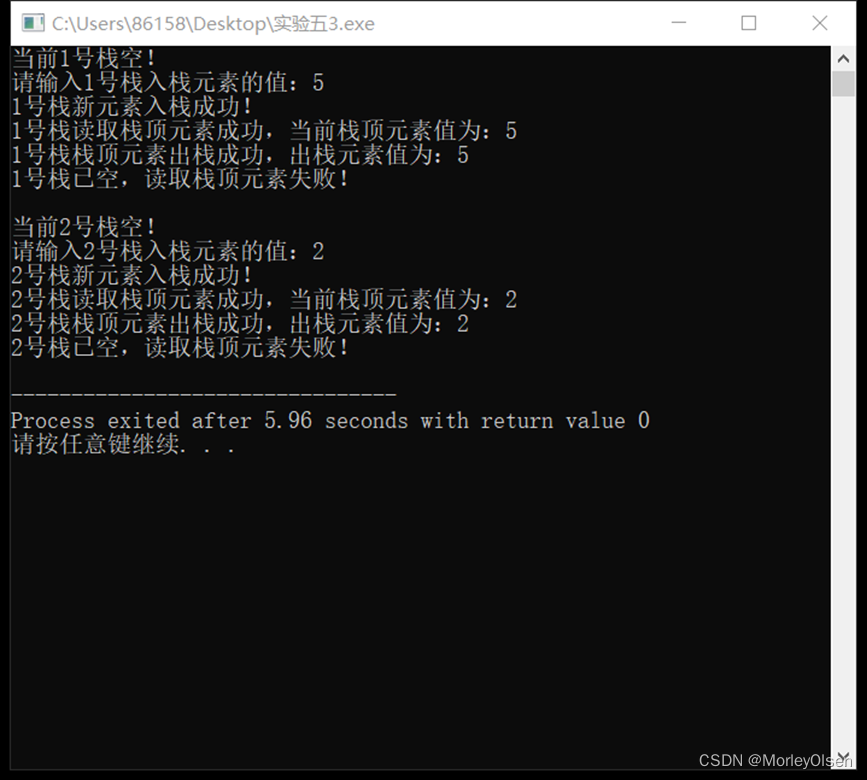
2）请分析你程序中每个功能模块的算法时间复杂度。

实验1：

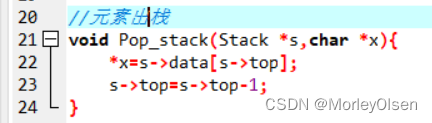
单元素出栈只需要锁定顶层的元素即可。所以，时间复杂度为O(1)。

单元素入栈只需要对顶层进行元素覆盖即可。所以，时间复杂度为O(1)。

假设字符串长度为len，那么多元素入栈需要执行len次。所以，时间复杂度为O(n)。

本段代码通过对入栈后的字符串反向出栈进行判断，即出栈的第一个元素是原来字符串的最后一个元素。我们可以令出栈的第一个元素与原字符串的第一个元素进行对比，来判断该字符串对应的数字是否为回文数。所以，时间复杂度为O(n)。

实验2：

出栈、入栈等操作沿用实验1的结果，这里不再赘述。

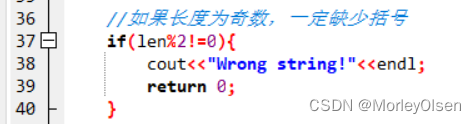
当输入的符号字符串长度为奇数的时候，一定有一个括号落单，即一定不可能为合法的输入。符号字符串的长度为偶数是必要不充分条件，因此直接否定奇数长度可减少算力。所以，时间复杂度为O(1)。

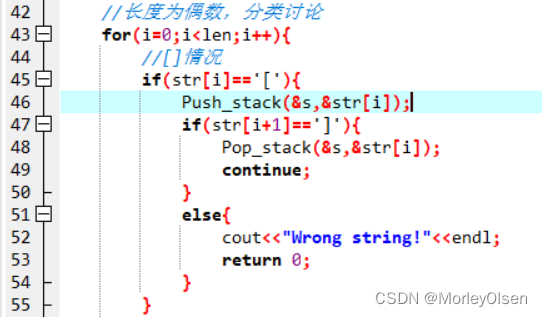
本段算法通过循环先对当前的字符进行判断，再对下一个邻近的字符进行判断，即判断相邻两个括号是否为合法输入。整个过程需要对字符串每一个位置的字符进行判断。所以，时间复杂度为O(n)。

实验3：

判断栈是否为空栈，只需要判断顶指针是否处于-1位置。所以，时间复杂度为O(1)。

新元素入栈的时候，先要判断共享栈是否已满。如果共享栈非满，那么在下一个位置插入一个元素，顶指针同时移动到该位置。所以，时间复杂度为O(1)。

新元素出栈的时候，先要判断共享栈是否已空。如果共享栈非空，那么在当前位置弹出一个元素，顶指针同时移动到前一个位置。所以，时间复杂度为O(1)。

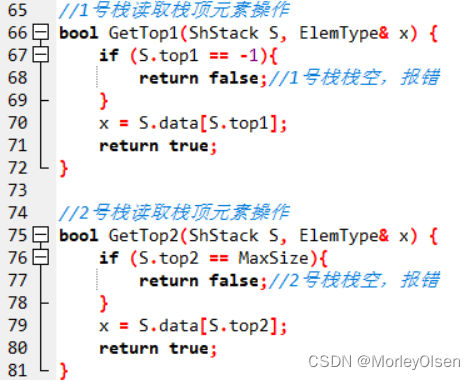
查看共享栈的两个栈顶元素时，只需要在保证两个栈非空的情况下，对顶指针所指向的元素进行查看。所以，时间复杂度为O(1)。

其他：

#include<iostream>
#include<cstring>
#define STACK_INIT_SIZE 100
#define STACK_INCREMENT 10
using namespace std;
 
typedef struct SqStack {
 char *elem;
 int top;
 int stacksize;
}SqStack;
 
//初始化栈，容量是事先定义好的，定义初始的top标号为-1.
void InitStack(SqStack& S)
{
 S.elem = new char[STACK_INIT_SIZE];
 if (!S.elem)
  cout << "Overflow!" << endl;
 S.top = -1;
 S.stacksize = STACK_INIT_SIZE;
}
 
//该函数用来释放栈的空间
void DestroyStack(SqStack& S)
{
 delete[]S.elem;
 S.top = -1;
 S.stacksize = 0;
}
 
//若栈已满，该函数用来增加栈的空间
void increment(SqStack& S)
{
 char *newstack = new char[S.stacksize + STACK_INCREMENT];
 if (!newstack)
  cout << "Overflow!" << endl;
 for (int i = 0; i <= S.top; i++)
 {
  newstack[i] = S.elem[i];
 }
 delete[]S.elem;
 S.elem = newstack;
 S.stacksize += STACK_INCREMENT;
}
 
//该函数用来往栈里面增添元素，因为是入栈，所以栈顶元素的位置数加一，该元素成为新的栈顶元素
void Push(SqStack& S, char e)
{
 if (S.top == S.stacksize - 1)
  increment(S);
 S.elem[++S.top] = e;
}
 
//该元素用来返回栈顶元素的值
char GetTopStack(SqStack& S)
{
 if (S.top == -1)
  cout << "Empty!" << endl;
 return S.elem[S.top];
}
 
//该函数用来将元素出栈
void Pop(SqStack& S)
{
 if (S.top == -1)
  cout << "Empty!" << endl;
 S.top--;
}
 
//主函数：将字符串的长度len对2取模记为mid，将前mid个字符入栈。若该字符串回文：先给标志赋值为0，如果len为偶数，则第mid+1个元素应和栈顶元素相同，如果不同就直接退出循环，将标志的值改为1；相同就将元素出栈，判断下一个字符和栈顶元素是否相等，以此类推。如果len为奇数，则最中间的元素和其它元素都不同，跳过这个元素继续向下判断。最后通过标志的值判断该字符串是否回文：如果标志的值被修改，说明对称的两元素不相同，则字符串不回文。
int main()
{
 SqStack s;
 InitStack(s);
 char str[1000];
 cin >> str;
 int len = strlen(str);
 int mid = len / 2;
 int i, flag = 0;
 for (i = 0; i < mid; i++)
 {
  Push(s, str[i]);
 }
 if (len % 2 == 1)
  i++;
 while (i<len)
 {
  if (GetTopStack(s) != str[i])
  {
   flag = 1;
   break;
  }
  i++;
  Pop(s);
 }
 if (flag)
 {
  cout << "该字符向量不是回文！" << endl;
 }
 else
 {
  cout << "该字符向量是回文！" << endl;
 }
 return 0;
}

#include<iostream>
#include<cstring>
#define STACK_INIT_SIZE 100
#define STACK_INCREMENT 10
using namespace std;
 
typedef struct SqStack {
 char* elem;
 int top;
 int stacksize;
}SqStack;
 
//初始化栈，容量是事先定义好的，定义初始的top标号为-1.
void InitStack(SqStack& S)
{
 S.elem = new char[STACK_INIT_SIZE];
 if (!S.elem)
  cout << "Overflow!" << endl;
 S.top = -1;
 S.stacksize = STACK_INIT_SIZE;
}
 
//该函数用来释放栈的空间
void DestroyStack(SqStack& S)
{
 delete[]S.elem;
 S.top = -1;
 S.stacksize = 0;
}
 
//若栈已满，该函数用来增加栈的空间
void increment(SqStack& S)
{
 char* newstack = new char[S.stacksize + STACK_INCREMENT];
 if (!newstack)
  cout << "Overflow!" << endl;
 for (int i = 0; i <= S.top; i++)
 {
  newstack[i] = S.elem[i];
 }
 delete[]S.elem;
 S.elem = newstack;
 S.stacksize += STACK_INCREMENT;
}
 
//该函数用来往栈里面增添元素，因为是入栈，所以栈顶元素的位置数加一，该元素成为新的栈顶元素
void Push(SqStack& S, char e)
{
 if (S.top == S.stacksize - 1)
  increment(S);
 S.elem[++S.top] = e;
}
 
//该元素用来返回栈顶元素的值
char GetTopStack(SqStack& S)
{
 if (S.top == -1)
  cout << "Empty!" << endl;
 return S.elem[S.top];
}
 
//该函数用来将元素出栈
void Pop(SqStack& S)
{
 if (S.top == -1)
  cout << "Empty!" << endl;
 S.top--;
}
 
//主函数：输入字符串，向后遍历，如果元素是左括号则将左括号入栈，如果元素是右括号，则将左括号弹出栈顶，这样可以继续判断下一个左括号是否和右括号匹配。一旦右括号和左括号匹配不成功，那么修改标志表示括号匹配失败。其中，需要一开始就将‘#’压入栈，如果最后字符串遍历完了（也就是左括号都被消解完了）栈顶元素是‘#’，说明左括号和右括号匹配上不多不少刚刚好。
int main()
{
 SqStack s;
 int flag = 1;
 InitStack(s);
 Push(s, '#');
 char str[1000];
 cin >> str;
 int len = strlen(str);
 for (int i = 0; i < len; i++)
 {
  if (str[i] == '(' || str[i] == '[' || str[i] == '{')
   Push(s, str[i]);
  else
  {
   if (str[i] == ')')
   {
    if (GetTopStack(s) != '(')
    {
     flag = 0;
     break;
    }
    else
     Pop(s);
   }
   else if (str[i] == ']')
   {
    if (GetTopStack(s) != '[')
    {
     flag = 0;
     break;
    }
    else
     Pop(s);
   }
   else if (str[i] == '}')
   {
    if (GetTopStack(s) != '{')
    {
     flag = 0;
     break;
    }
    else
     Pop(s);
   }
  }
 }
 if (GetTopStack(s) != '#')
  flag = 0;
 if (flag)
  cout << "括号匹配成功！" << endl;
 else
  cout << "括号匹配失败！" << endl;
 return 0;
}

设top1和top2分别为栈1和2的栈顶元素的位置。

(1) 入栈主要语句

栈1的入栈语句：

if(top2-top1==1)

{

cout<<“栈满”<<endl;

exit(0);

}

SPACE[++top1]=x; //设x为入栈元素。

栈2的入栈语句：

if(top2-top1==1)

{

cout<<“栈满”<<endl;

exit(0);

}

SPACE[--top2]=x;

出栈主要语句

栈1的出栈语句:

if(top1==-1)

{

cout<<“栈空”<<endl;

exit(0);

}

top1--;

return(SPACE[top1+1]); //返回出栈元素。

栈2的出栈语句:

if(top2==N)

{

cout<<“栈空”<<endl;

exit(0);

}

top2++;

return(SPACE[top2-1]);

  1. 栈满条件:top2-top1=1

栈空条件:top1=-1并且top2=N //top1=-1为左栈空,top2=N为右栈空

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/799653.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

揭秘全球最危险的11大网络间谍组织

揭秘全球最危险的11大网络间谍组织

根据安全研究人员的说法&#xff0c;下述这些都是全球最臭名昭著的&#xff0c;并且由民族国家资助的组织。 几十年前&#xff0c;当黑客入侵刚刚出现的时候&#xff0c;其大多是网络“发烧友”的“杰作”&#xff0c;他们痴迷于学习有关计算机和网络的一切知识。现如今&#x…
阅读更多...
2023年Q2京东黑电行业热门类目数据分析报告（京东大数据）

2023年Q2京东黑电行业热门类目数据分析报告（京东大数据）

随着家电行业的日趋成熟&#xff0c;黑电市场也愈加繁荣&#xff0c;黑色家电包括电视、音响、家庭影院、摄像机、游戏机等等带给人们娱乐的电器。 目前来看电视机在黑电行业的占有份额较大&#xff0c;而前面我们已经分析过电视市场&#xff0c;接下来我们继续一起来分析除电视…
阅读更多...
实现PC端微信扫码native支付功能

实现PC端微信扫码native支付功能

目录 实现PC端微信扫码 简介 实现步骤 1. 获取商户号 2. 生成支付二维码 3. 监听支付结果 4. 发起支付请求 5. 处理支付回调 示例代码 结论 Native支付 Native支付的工作原理 Native支付的优势 Native支付的应用和市场地位 开通使用微信 native 支付流程 步骤一…
阅读更多...
LaTeX Error: File `tabu.sty‘ not found.

LaTeX Error: File `tabu.sty‘ not found.

虽然Miktex可以自动下载和安装没有的库&#xff0c;但有些时候也有可能会直接报错&#xff1a; LaTeX Error: File tabu.sty not found. 解决方法就是打开控制台。然后手动下载&#xff1a;
阅读更多...
Sharding-JDBC分布式事务详解与实战

Sharding-JDBC分布式事务详解与实战

&#x1f680; ShardingSphere &#x1f680; &#x1f332; 算法刷题专栏 | 面试必备算法 | 面试高频算法 &#x1f340; &#x1f332; 越难的东西,越要努力坚持&#xff0c;因为它具有很高的价值&#xff0c;算法就是这样✨ &#x1f332; 作者简介&#xff1a;硕风和炜&…
阅读更多...
最强，Python接口自动化测试-自动化用例编写（超细整理）

最强，Python接口自动化测试-自动化用例编写（超细整理）

目录&#xff1a;导读 前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结&#xff08;尾部小惊喜&#xff09; 前言 我们在百度搜索天…
阅读更多...
从 7 分钟到 10 秒，Mybatis 批处理太强了！

从 7 分钟到 10 秒，Mybatis 批处理太强了！

这篇文章会一步一步带你从一个新手的角度慢慢揭开批处理的神秘面纱&#xff0c;对于初次写Mybatis批处理的同学可能会有很大的帮助&#xff0c;建议收藏点赞~ 处理批处理的方式有很多种&#xff0c;这里不分析各种方式的优劣&#xff0c;只是概述 ExecutorType.BATCH 这种的用…
阅读更多...
打印插件 hiprint 使用、回单打印PDF保存本地、将列表数据打印成pdf文件保存到本地

打印插件 hiprint 使用、回单打印PDF保存本地、将列表数据打印成pdf文件保存到本地

文章底部有个人公众号&#xff1a;热爱技术的小郑。主要分享开发知识、有兴趣的可以关注一手。 前言 最近做了一个回单打印的功能、核心功能是、渲染出来的回单列表&#xff0c;用户可以浏览回单数据。可以同时勾选多个要打印的回单数据。将回单打印成pdf文件、同时下载保存到…
阅读更多...
多线程进阶篇----常用方法

多线程进阶篇----常用方法

文章目录 线程状态线程方法线程礼让线程优先级守护线程 线程同步生产者消费者问题解决方式一&#xff1a;管程法方法二&#xff1a;标志位法 死锁总结 线程状态 线程有5种状态&#xff0c;新生态、就绪态、阻塞态、运行态、死亡态 在该图上&#xff0c;就绪状态和运行状态是一…
阅读更多...
webpack联邦模块介绍及在dumi中使用问题整理

webpack联邦模块介绍及在dumi中使用问题整理

提示&#xff1a;文章写完后&#xff0c;目录可以自动生成&#xff0c;如何生成可参考右边的帮助文档 文章目录 前言一、ModuleFederationPlugin参数含义&#xff1f;二、如何在dumi中使用及问题整理1. 如何在dumi中使用(这个配置是好使的)2.相关问题整理2.1 问题12.2 问题2 总…
阅读更多...
Android 之 动画合集之属性动画 -- 初见

Android 之 动画合集之属性动画 -- 初见

本节引言&#xff1a; 本节给带来的是Android动画中的第三种动画——属性动画(Property Animation)&#xff0c; 记得在上一节Android 之 动画合集之补间动画为Fragment 设置过渡动画的时候&#xff0c;说过&#xff0c;App包和V4包下的Fragment调用setCustomAnimations()对应…
阅读更多...
白皮书精彩案例分享 | 数字孪生：让治水用水有了“智慧大脑”

白皮书精彩案例分享 | 数字孪生：让治水用水有了“智慧大脑”

山有百藏而不言&#xff0c;水润万物而不语。中国属于大河文明&#xff0c;农业历来在经济中占主导地位&#xff0c;其中水利灌溉是保证农业生产和提高农业产量的重要因素。 然而&#xff0c;由于过去水利工程建设缺乏预见性&#xff0c;传统水利工程在作出贡献的同时&#xf…
阅读更多...
JavaScript 简单实现观察者模式和发布订阅模式

JavaScript 简单实现观察者模式和发布订阅模式

JavaScript 简单实现观察者模式和发布订阅模式 1. 观察者模式1.1 如何理解1.2 代码实现 2. 发布订阅模式2.1 如何理解2.2 代码实现 1. 观察者模式 1.1 如何理解 概念&#xff1a;观察者模式定义对象间的一种一对多的依赖关系&#xff0c;当一个对象的状态发生改变时&#xff…
阅读更多...
重生之我要学C++第三天（类和对象）

重生之我要学C++第三天（类和对象）

我重生了&#xff0c;这篇文章就深入的探讨C中的类和对象。 一.类的引入和定义 类的引入&#xff1a;在C语言中&#xff0c;结构体内部只能定义变量或者结构体&#xff0c;C中对结构体进行了升级->类&#xff0c;C的类中既可以定义变量&#xff0c;又可以定义函数。类中的变…
阅读更多...
TSINGSEE青犀视频安防监控视频平台EasyCVR新增密码复杂度提示

TSINGSEE青犀视频安防监控视频平台EasyCVR新增密码复杂度提示

智能视频监控平台TSINGSEE青犀视频EasyCVR可拓展性强、视频能力灵活、部署轻快&#xff0c;可支持的主流标准协议有国标GB28181、RTSP/Onvif、RTMP等&#xff0c;以及支持厂家私有协议与SDK接入&#xff0c;包括海康Ehome、海大宇等设备的SDK等&#xff0c;能对外分发RTSP、RTM…
阅读更多...
BERT模型和Big Bird模型对比

BERT模型和Big Bird模型对比

BERT模型简介 BERT模型是基于Transformers的双向编码器表示&#xff08;BERT&#xff09;&#xff0c;在所有层中调整左右情境&#xff08;学习上下层语义信息&#xff09;。 Transformer是一种深度学习组件&#xff0c;能够处理并行序列、分析更大规模的数据、加快模型训练速…
阅读更多...
sftp和scp协议，哪个传大文件到服务器传输速率快？

sftp和scp协议，哪个传大文件到服务器传输速率快？

环境&#xff1a; 1.Win scp 6.1.1 2.XFTP 7 3.9.6G压缩文件 4.Centos 7 5.联想E14笔记本Win10 6.HW-S1730S-S48T4S-A交换机 问题描述&#xff1a; sftp和scp协议&#xff0c;哪个传大文件到服务器速度快&#xff1f; 1.SFTP 基于SSH加密传输文件&#xff0c;可靠性高&am…
阅读更多...
Profinet转EtherNet/IP网关连接AB PLC的应用案例

Profinet转EtherNet/IP网关连接AB PLC的应用案例

西门子S7-1500 PLC&#xff08;profinet&#xff09;与AB PLC以太网通讯&#xff08;EtherNet/IP&#xff09;。本文主要介绍捷米特JM-EIP-PN的Profinet转EtherNet/IP网关&#xff0c;连接西门子S7-1500 PLC与AB PLC 通讯的配置过程&#xff0c;供大家参考。 1, 新建工程&…
阅读更多...
护网行动：ADSelfService Plus引领企业网络安全新纪元

护网行动：ADSelfService Plus引领企业网络安全新纪元

随着信息技术的飞速发展&#xff0c;企业网络的重要性变得愈发显著。然而&#xff0c;随之而来的网络安全威胁也日益增多&#xff0c;网络黑客和恶意软件不断涌现&#xff0c;给企业的数据和机密信息带来巨大风险。在这个信息安全威胁层出不穷的时代&#xff0c;企业急需一款强…
阅读更多...
API攻击原理，以及如何识别和预防

API攻击原理，以及如何识别和预防

攻击者知道在针对API时如何避开WAF和API网关。以下是一些公司应对API攻击快速增长的示例。 5月初&#xff0c;Pen Test Partners 安全研究员 Jan Masters 发现&#xff0c;他竟然能够在未经身份验证的情况下&#xff0c;向Peloton的官方API提出可获取其它用户私人数据的请求&am…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023