博主:爱码叔
个人博客站点: icodebook.com
公众号:漫话软件设计
微博:程序员涛哥
专注于软件设计与架构、技术管理。擅长用通俗易懂的语言讲解技术。对技术管理工作有自己的一定见解。文章会第一时间首发在个站上,欢迎大家关注访问!
写在前面的话
今天我要开辟一个新的专栏,关于算法。算法的教材和文章相当的多,为什么我还要做这个专栏呢?
首先算法比较复杂,复杂在思想上,复杂在大量数学知识的运用上。因此市面上有些非常优秀的书,讲的很细,内容很全,但是门槛比较高。还有些算法书非常薄,但只讲了部分算法的思想,给出了实现代码而已。甚至连时间复杂度的 “O” 标记都没有解释。又让我觉得过于精简了。于是我萌生了写自己心目中算法应该怎么讲的文章。
再说说本专栏的文章形式。大概一年半前,我第一次尝试用漫画的形式创作了几篇关于安全的文章。
《图文结合彻底理解非对称加密、RSA原理及安全性》
《加密就像玩魔方----图文详解对称加密》
《图文轻松理解计算机网络五层架构》
反响还不错。于是我想尝试挑战用漫画的形式创作算法专栏。
虽然工作中很少使用算法,但却是程序员的必须课。希望看我的算法专栏能让读者更为轻松的学习到算法知识!
专栏的内容会参考《算法导论》、《算法》等经典著作,将里面经典的内容以通俗易懂的形式,并辅以大量插图呈现给大家。
文章中有两位虚拟人物:
- 经验丰富的老司机程序员----熊小猫
- 初入职场激情满满的菜鸟程序员----兔小白
让我们跟随兔小白和熊小猫一起走入算法的世界!
下面开始第一篇正文
边打扑克边学插入排序算法,彻底搞懂时间复杂度
什么是算法、什么是时间复杂度、时间复杂度中的O标记是什么意思、如何分析算法的时间复杂度?咱们跟着兔小白和熊小猫,边打扑克边学!基础知识掌握好,后面学到复杂算法才会更从容!

熊小猫:晚上放松下,来我家打牌怎么样?
兔小白:不去了,我已经计划从今晚开始学习算法
熊小猫:在游戏中学习效果最好!其实抓牌的过程就存在一个算法!
兔小白:哦!?难道有抓到好牌的算法?
熊小猫:想什么呢!你说的是出老千!
兔小白:嘿嘿…
熊小猫:抓牌时候是不是要按顺序排放你手中的牌?这里就用到了插入排序。
兔小白:啊,之前我面试挂了,考的就是插入排序!没想到我打了20年扑克牌,竟然一直都在实践插入排序!?
熊小猫:今晚打完扑克,包你彻底掌握插入排序!
插入排序如何工作
下班后,兔小白来到了熊小猫家里打扑克。
兔小白:来吧!讲讲插入排序,请开始你的表演!
熊小猫:别着急,我先发牌。发完后,你再摸牌。边摸边思考下摸牌的过程。
兔小白:手里的牌需要从小到大排列,每次我摸牌后都会从小的一侧开始比较,直到找到比我抓到的牌大的那一张,然后插在那一张牌的前面

熊小猫:没错!这就是插入排序。我们仔细看看这个过程。

熊小猫:插入排序是不是很简单?你看看能不能用代码实现?
兔小白:等等!我的牌不错,先打完这局!
插入排序代码
熊小猫:你这牌也太好了,我认输了。
兔小白:作为惩罚,再给我讲讲代码实现吧?
熊小猫:没问题!咱先写一种最自然地,符合我们直觉地摸牌算法。首先你从牌堆里抓出一张牌,然后从左向右和手牌进行比较,找到比你抓到的牌大的那一张,你会把这张牌插入到它的前面。如果找到手牌的牌尾还没找到,那么放到牌尾。
兔小白:我想想…没错,确实我抓牌时候非常自然地就是这么做的! 但从你嘴里以这么严谨的逻辑说出来,我还得理解一下,嘿嘿!
熊小猫:那我们就按照这个逻辑写代码。
public static Integer[] sort(Integer[] unsorted) {
//sorted数组可以理解为拿着排好序手牌的"手"
Integer[] sorted = new Integer[unsorted.length];
//第一张牌什么都不用想,放入手中
sorted[0] = unsorted[0];
//从第二张牌开始要逐张找到其顺序的位置放入
for (int i = 1; i < unsorted.length; i++) {
//摸起一张牌,从左侧开始比较,找到插入的位置。最差的情况要找到手牌的牌尾
for (int j = 0; j <= i; j++) {
//如果已经找到手牌牌尾或者中途找到手牌中比当前牌大的那张牌
if (j==i || unsorted[i] < sorted[j]) {
//比当前大的那张牌以及后面的牌向后移一位
for (int k = i-1; k >= j; k--) {
sorted[k + 1] = sorted[k];
}
//将当前牌放入移动后空出来的那个位置。
sorted[j] = unsorted[i];
//本轮结束
break;
}
}
}
return sorted;
}
兔小白:注释都有了!但我还是看不太懂。
熊小猫:其实很好理解,咱们跟着注释一行行的看。
- 函数的输入是一个无序的整型数组 unsorted,可以理解为桌面牌堆
- 第3行初始化的整型数组 sorted,可以理解为你的“手”,用来放排好序的牌。这里记住,手中牌是 sorted 中放的牌,桌面牌堆是 unsorted 中放的牌。
- 第5行代码是你抓出第一张牌时,手里还是空的。所以直接放入你的手里,也就是 sorted 的0号位置。
- 第7行开始进入主要的算法逻辑。从第二张牌开始,逐一找到自己的位置放进来。直到抓完所有的牌,也就是循环完 unsorted。
- 摸起一张牌 unsort[i],然后从左向右,和手中牌比较大小。摸起的是第 i 张牌时,你手中有 i-1 张牌。但最差的情况要比较 i 次,因为如果很不幸,你拿到的牌比手里的 i-1 牌都大,要再比较一次以判断是否走到现有手牌的牌尾。(第9行代码)
- 第 11 行代码,就是在比较摸起的牌和手里的牌,目的是找到比摸起的牌大的牌的位置 j。条件语句中的 j==i 表示找到手牌牌尾也没有找到比摸到的牌更大的牌。
- 13-15 行这个循环体做的事情是,将 sorted 中 j 位置后面的牌往后移一位,空出 j 这个位置,用来放摸到的牌。
- 17 行代码便是将抓的牌 放入手中正确的位置 sorted[j]
- 19 行的 break 表示一轮插入逻辑结束,也就是第 9 行的 for 循环结束。此时已经将这次抓到的牌放入手牌中正确位置。
如此往复 4.1~4.5,直到所有 unsorted 中的元素都有序的放入 sorted。
兔小白:代码逻辑和我抓牌时脑子里想的一模一样!!我脑子只是转了一下,代码表达出来居然写了这么多?
熊小猫:哈哈,别看代码多,但计算机执行起来可比你脑子快的多!
兔小白:我突然想到有时候我会先把牌堆的牌全拿到手中再排顺序。这样排序会不会更快?
熊小猫:这个问题的本质是如何评价算法,解决问题的办法不止一种,如何评价哪种更好呢?通常我们使用算法复杂度来评价算法。
兔小白: 算法复杂度?说来听听?
熊小猫:别急,上面我给出的算法并不是最经典的插入排序。我再送你一份经典的插入排序代码,加量不加价!这个算法就是你说的把牌全部拿到手中再排序,这样就只需一个数组,节省了存储空间。
算法的主要逻辑是,从第二个元素开始,和前面的元素逐一比较,如果自己较小,就和前面的交换位置,然后再继续和前面的比较。直到找到前面比自己还小的那个元素,就停在当前的位置,然后开始下一轮循环。
代码如下,你先自己研究下,看明白后加上注释。
public static Integer[] sortV2(Integer[] unsorted) {
for (int i = 1; i < unsorted.length; i++) {
for (int j = i; j > 0 && unsorted[j] < unsorted[j - 1]; j--) {
Integer toBeSortedNumber = unsorted[j];
unsorted[j] = unsorted[j - 1];
unsorted[j - 1] = toBeSortedNumber;
}
}
return unsorted;
}
兔小白:考我是吧?就这几行代码,五分钟搞定!
五分钟后兔小白给代码加上了注释
public static Integer[] sortV2(Integer[] unsorted) {
//从第二个元素开始,向后逐一执行排序逻辑
for (int i = 1; i < unsorted.length; i++) {
//从待排序元素的位置开始,向前逐一比较。比自己大就交换位置,比自己小停止循环。
for (int j = i; j > 0 && unsorted[j] < unsorted[j - 1]; j--) {
//如果前一个元素比当前元素大,那么交换两个元素的位置
Integer toBeSortedNumber = unsorted[j];
unsorted[j] = unsorted[j - 1];
unsorted[j - 1] = toBeSortedNumber;
}
}
return unsorted;
}
熊小猫:这个代码是不是简洁多了。下面咱们再聊聊算法的复杂度。
如何评价算法?
兔小白:我经常听别人讨论算法复杂度。什么是算法复杂度?是算法代码的行数吗?
熊小猫:代码行数?你别闹。。。通常算法复杂度包括时间复杂度和空间复杂度。下面我慢慢解释。
算法用来解决问题。生活中也有各种各样的问题要解决。比如我从北京开车去北戴河应该怎么走。线路的选择有很多。有的路程虽然远,但是车少、路好走,所以时间短。有的路程虽然近很多,但是车多拥堵,导致时间反而更长。

看完这个例子,如何评判算法优劣,相信我们心里已经有数。
首先是算法的速度,也就是解决问题所消耗的时间。这就是我们常说的“时间复杂度”
然后是算法消耗的资源,例子中是公路,资源是要付出代价的,体现在油费和高速费。对于算法来说,运算中消耗的资源是计算机的存储。计算过程中使用的存储数量,就是 “空间复杂度”。
你一定听说过“以时间换空间”或者“以空间换时间”。算法中的也有这个概念,牺牲更大的存储空间换取更短的运算时间,或是以更长的运算时间换取更小的存储使用。
究竟是时间优先还是空间优先,这取决于你手里的资源。如果你想更快到达北戴河,甚至可以乘坐直升飞机,但是成本飙升。我们永远渴望更快的运算速度,但是又被成本所牵制。不过在这个存储非常廉价的时代,可以更多考虑运算时间。
除了时间复杂度和空间复杂度外,还可以从以下几个方面评价算法的优劣。
- 易读性。代码是否简洁、易读,便于维护。从工程角度看,这一点非常重要。
- 健壮性。对于非法输入是否有足够的包容性。
- 安全性。算法是否有安全漏洞,可以被利用、攻击。尤其是安全相关的算法。
这几点主要在工程实践、非功能性需求等方面对算法提出近一步要求。
我们回归到算法本身,算法的评判标准是时间复杂度和空间复杂度。
时间复杂度
熊小猫:正如汽车的性能不一样,计算机的性能也不一样。对于时间的度量,需要在统一标准的机器上进行。我们假设这台机器基本的指令(算术、移动、控制)都能在常量时间内运行完成。
算法运行的时间一般和输入规模同步增长。10牌排序肯定快于50张牌。因此,一般将运算时间用输入规模的函数表达。
咱们看个很简单的例子。还是打扑克,我现在出 K,你需要出比K大的牌管上我。假设这个扑克牌玩法只能单张出牌,每人手里10张牌(虽然很愚蠢,但能简化理解),并且已经排好序。这里给出一个最直观地出牌算法:从第一张开始逐张进行比较,如果小于等于 K,继续比较下一张,直到找到大于 K 的牌打出此牌。如果找到牌尾没有找到,则告知对方不出牌。
假设你手里有n张牌,那么输入规模就是n。每次比较所消耗的时间是 t1,找到牌后选择出牌或者告知对方不出牌消耗时间t2。我们考虑最差的情况,会比较完手里的所有牌。此时消耗的时间是n*t1,算法的时间函数如下。
T(n) = t1*n + t2
这是一个非常精准的时间计算。但在计算机领域,我们更关心的是运行时间随 n 的增长率或者增长量级。因此可以忽略掉常数项、低阶项、常数系数。我们可以看个例子感受一下。
假设我们有另外一个出牌算法,时间函数为
T’(n) = c1*n^2+c2
即使 t1 比 c1 大很多,t2 也比 c2 大很多,也终究无法改变一个事实:当 n 足够大时,T‘(n) 将永远超越T(n)。通过下面这个示意图可以直观的感受这个结论。

可以看出常数项和常数系数并不重要。因此,我们比较算法的时间复杂度时,通常将常数项以及常数系数忽略掉。但不可以将 T(n) = t1*n + t2 转化为 T(n) = n 。正确的写法是 T(n) = O(n)。
兔小白:我理解函数的最高阶项决定了他的增长量级,低介项和常量系数可以忽略。
熊小猫:没错,理解的很到位!
兔小白:但是这个 “大欧” 是什么符号?我确实见过 T(n) = O(n) 这种写法,不过一直不理解。
熊小猫:别急,接下来我们就看看记号 “大欧”。
O记号
熊小猫:“大欧” 用来标记一个函数的渐进上界。前面讲过算法时间函数的增长量级可以用来比较算法的时间复杂度。那么渐进上界和增长量级是一回事吗?我们先来看看什么是渐进上界。
看下图的两个函数 f(n)=t1*n + t2 及 g(n)=n。

当我们将g(n)乘以一个大于1的系数c,得到一个新的函数cg(n)。

可以看到在相交点 n0 后,对于所有 n ,都有 cg(n)>f(n)。这就是渐进上界的定义。对于给定的函数 g(n), 如果存在正常量 c和n0 使得 对所有 n>n0, 有 0<=f(n)<=cg(n),那么 g(n) 就是 f(n) 的渐进上界。 记作 f(n)=O(g(n))。
单看文字定义,你一定云里雾里。我们来看上面的图,当g(n)乘以一个大于0的系数c后,cg(n)的线会比f(n)更为陡峭,这意味着在某个点n0,cg(n)的线将永远在f(n)的上方。
兔小白:等等,这里我有个问题,根据渐进确界的定义,t1*n + t2=O(n^2) 也是成立的,你看下面我画的图,完全符合定义!

但是 t1 * n^2+ t2 的渐进上界也是 O(n^2) 。那么渐进上界就无法用来比较时间复杂度。
熊小猫:这个问题非常非常好!渐进上界并不能准确描述一个函数的增长量级。其实很多算法书中将O用作标记渐进紧确界(标准的标记应该用Θ)。渐进紧确界除了满足渐进上界的要求之外,还需要存在c‘使得所有 n>n0, 有cg(n)>f(n)>c’g(n)。 文字太抽象,还是看图吧。

函数 cn^2,即使c再小,终究还是会高过 t1n + t2 。所以 g(n)=n^2 不满足对 f(n)= t1*n + t2 的渐进紧确界的定义。但函数 g(n)=n 满足定义,因此 n=O(n) 成立,但 n=O(n^2) 是错误的。
兔小白:明白了,我们通常看的算法书中把O用作标记渐进紧确界而不是渐进上界。
熊小猫:没错,函数的渐进紧确界可以代表它的增长趋势。因为通过调整 g(n) 的系数 c 只能另函数曲线更陡峭或更平缓,但不会改变增长趋势。也就是说不会改变匀速增长、加速增长、减速增张的大趋势。
如果当n无穷大时,f(n)仍不能越界出 cg(n) 和 c‘g(n),而是被死死的夹住了。那么可以认为g(n)代表了f(n)的增长趋势,这就是为什么我们可以用T(n)的渐进紧确界来表示算法的时间复杂度。
兔小白:说实话数学这块把我搞得有点晕。虽然勉强能听懂,但用的时候恐怕又忘了。有没有简单的办法快速得到函数的渐进紧确界。
熊小猫:哈哈,这个其实最开始就说过了,通常来说,你把函数的常数项、低介项、常数系数去掉就可以了。
兔小白:这么简单?你看看我这几个算的对不对?
- an^2 + bn + c=O(n^2)
- nlgn+an+c = O(lgn)
熊小猫:第一个没问题,第二个错啦!应该是 O(nlgn)。n 并不是常数系数,需要保留。
兔小白:大意了!咱们说了半天还没说插入算法的时间复杂度呢。
熊小猫:别急,干任何事情都要打好基础,咱们这就看看插入算法的时间复杂度。
插入排序时间复杂度
熊小猫:基础打好了,我们来看看插入排序的时间复杂度。先问个问题,摸牌这个阶段的时间消耗每次都一样吗?
兔小白:当然不一样,有时候我着急就会摸的快一点!

熊小猫:不是这个意思…我是说每次找到插入位置所需的比较次数是固定的吗?
兔小白:当然不是,如果运气好,每次都比第一张牌小,那么每次都只需要比较一次。但是运气不好摸出一张比手里牌都大的牌,那么就要比较所有手里的牌,最后放到牌尾。
熊小猫:没错!如果牌堆里的牌是逆顺序排好,最大的牌在最上面,那么每次摸牌我都只需要比较一次。反之如果牌堆里的牌是顺序排好,最小的在最上面,那么每次摸牌都要比较手里所有的牌。
兔小白:碰到这种情况,我很快就会发现规律,我会改为从手中牌的右侧开始比。还是非常快!
熊小猫:你这已经改变算法啦!如果给算法加上智能,也不是不行,今天咱们不讨论这个。
我们讨论算法的时间复杂度,一般是看的最坏情况。也就是算法最长的运行时间。这和你评估工作量一样,3-5天的工作量,你肯定报5天。
兔小白:别提了,工作量我就没估准过,每次都是加班才搞定。
熊小猫:我们先计算算法消耗的总时间。算法中每个操作消耗的时间算然不同,但为常量。我们再分析出每个操作步骤执行的次数。两者相乘,得到一个步骤的总时长。再把所有操作步骤的消耗加起来就能得到运行时间的函数。另外由于消耗的时间是常量,根据渐进紧确界的特性,常量和常数系数是可以忽略的,那么我们只需要关心总的执行次数即可。
我们来分析第一版算法代码的运算次数。
public static Integer[] sort(Integer[] unsorted) {
Integer[] sorted = new Integer[unsorted.length];
sorted[0] = unsorted[0];
for (int i = 1; i < unsorted.length; i++) {
for (int j = 0; j <= i; j++) {
if (j==i || unsorted[i] < sorted[j]) {
for (int k = i-1; k >= j; k--) {
sorted[k + 1] = sorted[k];
}
sorted[j] = unsorted[i];
break;
}
}
}
return sorted;
}
2行:1
3行:1
4行:n
5行 :从i=1到n-1,累加ti,
6行: 从i=1到n-1,累加ti
7行:从i=1到n-1,累加 i-ti+1
8行:从i=1到n-1,累加 i-ti+1
10行:n-1
11 行:n-1
2,3,4 行执行次数很好理解。在第 5 行的 for 循环体中,如果找到了 unsorted[i] 的位置,并放置好后会跳出循环,但查找所用的次数是无法确定的,我们用ti表示。由于要从 i=1 执行到 i=n-1,所以第5,6行代码代码执行的次数为从i=1到n-1,累加ti。
再看 7,8 行。这段代码逻辑是将找到 unsorted[i] 插入位置及之后的元素往后移动一个位置。找到unsorted[i] 插入的位置我们用了 ti 次比较。插入位置为 ti-1。此时手中牌最后一张牌的位置为 i-1。那么需要移动的牌的数量为 i-1-(ti-1)+1,即为 i-ti+1。

由于数组下标从0,而不是1开始,所以会出现+1或-1,做成一些理解上的困难。其实你只要理解原理:移动的次数=当前手里牌的数量-(比较的次数-1)。
而且之前也提到过,时间复杂度其实只和高阶项有关系,所以这里只要不出现阶的误差就不会影响大局。
根据分析我们列出时间函数。
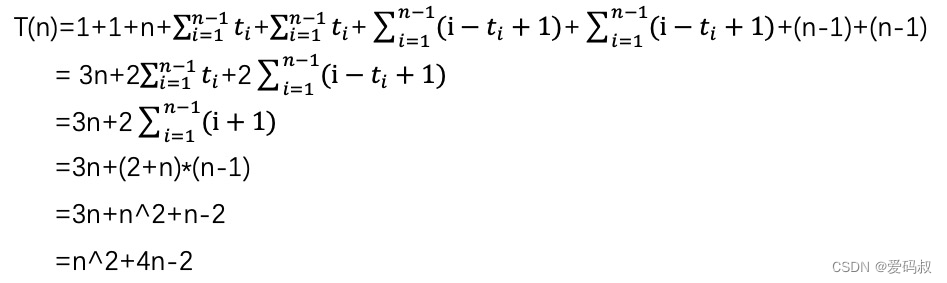
熊小猫:根据我们前面讲的内容,你来给出T(n)的渐进紧确界?
兔小白:这个简单,去掉常数项-2和低阶项4n,T(n)=O(n^2)。
熊小猫:可以啊,今晚扑克没白打!
兔小白:嗨,今晚光学习了,哪打扑克了。不过收获确实非常大!终于可以睡觉了!已经快12点了
熊小猫:别着急睡觉,你忘了还有经典的插入排序算法没有分析呢?
兔小白:让我来!我今天要看看凌晨四点半的北京!
熊小猫:你分析着,我先去睡觉了。明天还得上班呢。
public static Integer[] sortV2(Integer[] unsorted) {
for (int i = 1; i < unsorted.length; i++) {
for (int j = i; j > 0 && unsorted[j] < unsorted[j - 1]; j--) {
Integer toBeSortedNumber = unsorted[j];
unsorted[j] = unsorted[j - 1];
unsorted[j - 1] = toBeSortedNumber;
}
}
return unsorted;
}
兔小白:看着不难,争取半小时后睡觉!
一小时后…
兔小白:时间复杂度搞定了!
2行: n
3行:从 i=1 到 n-1,累加ti,
4,5,6行:均为从 i=1 到 n-1,累加 ti-1,
由于循环体跳出需要多判断一次,所以假如第三行是 ti 次,那么 4,5,6 行 为 ti-1。时间函数如下:
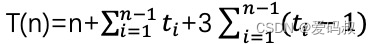
ti 的取值不确定。最好的情况是牌的顺序已经排好,每次只需要比较1次,并且不需要交换元素位置,ti都是1。时间复杂度如下:
T(n) = n + 1*(n-1)=2n-1=O(n)
最差的情况牌为倒序,每一轮都要和排好序的牌全部交换一次才结束。所以交换的次数为i,比较的次数多一次为i+1。我们把 ti=i+1 带入计算。
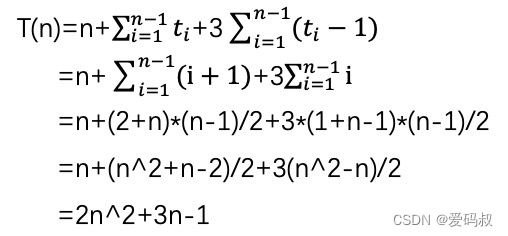
这种写法不但在最好的情况下时间复杂度是线性的,而且代码简洁,还省内存。看来写出正确的算法并不难,难的是写出好算法!终于可以踏实睡觉了!