实验九 二叉树
一、实验目的与要求
1)理解二叉树的类型定义;
2)掌握二叉树的存储方式及基于存储结构的基本操作实现;
二、 实验内容
1. 二叉树的结点定义如下:
struct TreeNode
{
int m_nvalue;
TreeNode* m_pLeft;
TreeNode* m_pRight;
};
输入二叉树中的两个结点,输出这两个结点在树中的最近公共祖先结点。
说明:最近公共祖先定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个结点也可以是它自己的祖先)。
2. 某同学非常喜欢玩二叉树。最喜欢的游戏是用结点中的大写字母构造查找二叉树。这是他构造的二叉树:
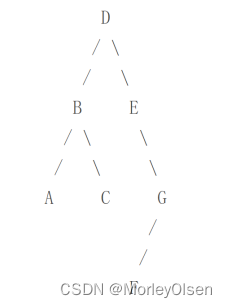
他为每棵树写下先序遍历和中序遍历两个字符串,例如:对于上面构造的树,先序遍历为DBACEGF,中序遍历为ABCDEFG。几年后,他想重新构造这棵树,请你来编写一个程序帮他实现基于上述遍历序列构造树。
题意解析:根据所给的两串序列,分别是前序和中序,求出二叉树的后序。
三、实验结果
1)简述算法步骤:
2)分析算法时间复杂度:
题目1:
0 实验代码及结果
#include <iostream>
#include <cstdio>
#include <vector>
using namespace std;
#define Max 100
vector<int> E[Max];
int parent[Max];
int depth[Max];
//构造递归的树 v->当前结点 p->当前的双亲结点 d->当前结点深度
void BuildTree(int v,int p,int d){
parent[v]=p;
depth[v]=d;
for(int i=0;i<E[v].size();i++){
if(E[v][i]!=p){
BuildTree(E[v][i],v,d+1);
}
}
}
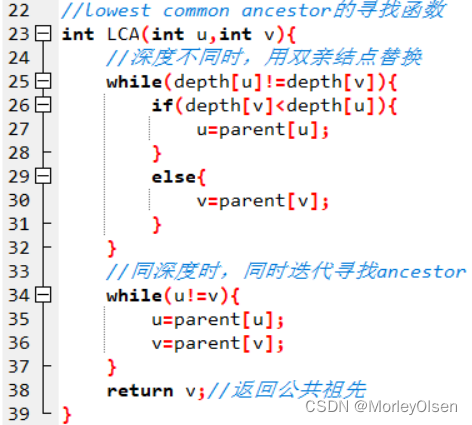
//lowest common ancestor的寻找函数
int LCA(int u,int v){
//深度不同时,用双亲结点替换
while(depth[u]!=depth[v]){
if(depth[v]<depth[u]){
u=parent[u];
}
else{
v=parent[v];
}
}
//同深度时,同时迭代寻找ancestor
while(u!=v){
u=parent[u];
v=parent[v];
}
return v;//返回公共祖先
}
int main(){
int n,root=1;//n->总结点数 root->根结点
//root需要定义!!!!!!!!!!!!!
cout<<"请输入总结点数:"<<endl;
cin>>n;
if(n==1){
cout<<"输入错误!不能只有一个结点!"<<endl;
return 0;
}
//i<n-1 根结点无双亲,所以少输入一次
for(int i=0;i<n-1;i++){
int u,v;
cout<<"请输入双亲结点编号及其孩子结点编号:"<<endl;
cin>>u>>v;
E[u].push_back(v);
E[v].push_back(u);
}
BuildTree(root,-1,0);//根结点双亲为-1,深度为0
int u,v;
cout<<"请输入两个待测结点的编号:" <<endl;
cin>>u>>v;
cout<<"其LCA为:"<<LCA(u,v)<<endl;
return 0;
}
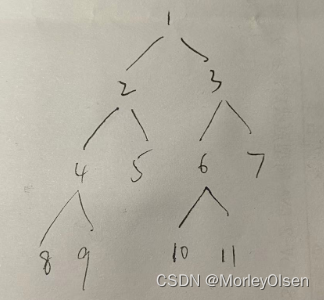
实验报告测试用例的二叉树如下图所示:
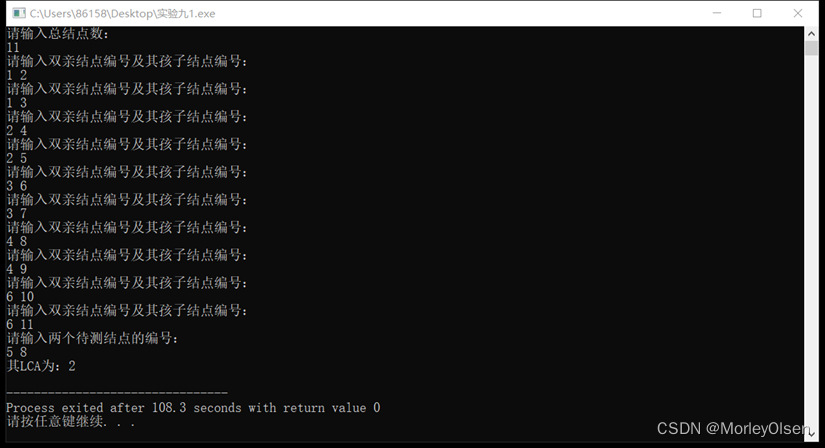
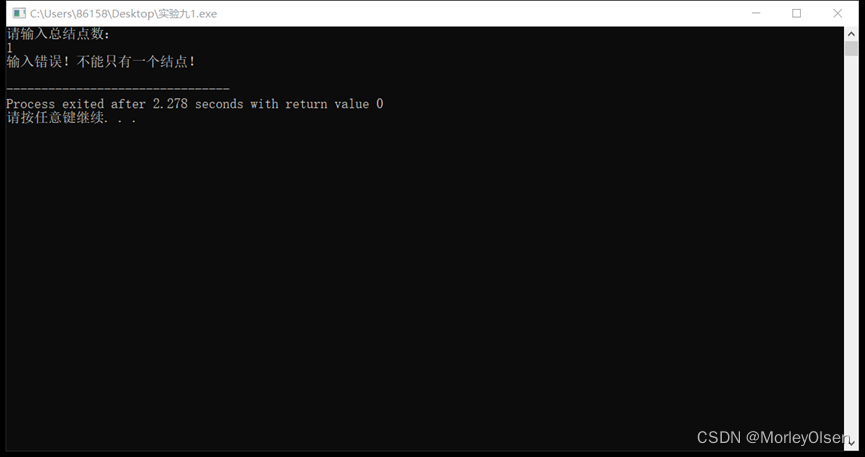
代码测试结果如下图所示:
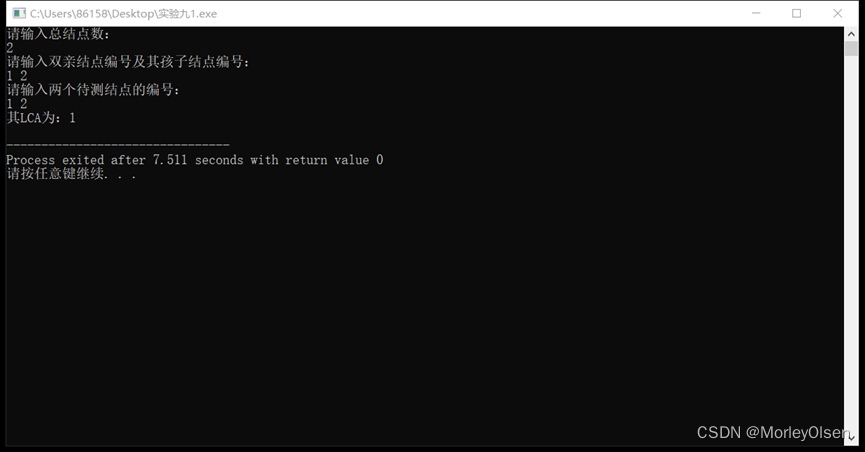
1 简述算法步骤
定义存储当前结点数据、双亲结点、当前结点深度的数组,并规定最大范围为100。

构造递归结构存储的数,存储当前结点的双亲结点和深度,然后通过for循环遍历,利用递归构造子树。在for循环中,如果遍历发现当前结点与双亲结点不同,即当前结点不是叶子结点,那么继续调用BuildTree函数构造子树,并将当前深度加一。

寻找最近公共祖先时,先判断两个结点的深度是否相同。如果深度不同,则先回溯深度较深的结点,寻找其与另外一个结点深度相同时的祖先。回溯完以后,此时u、v深度相同,直接比较u、v结点是否相同。如果结点不同,则分别向上回溯一个祖先,再判断其祖先是否相同。最后两个结点回溯到相同值,返回其中一个结点即可。
最后通过vector自带函数和for循环,将预设的树进行入栈并构造。

2 分析算法时间复杂度
在利用递归创建树时,利用了for循环遍历双亲合集,来判断当前结点的双亲结点是否已经被存入。由此可见,时间复杂度为O(n^2)。

在LCA函数中,通过第一个while循环收缩较远结点的深度进行回溯,通过第二个while循环同时收缩两个结点的深度进行回溯。由此可见,时间复杂度均为O(n)。

在主函数输入预设树的基本信息时,利用了for循环将每一组【双亲结点+孩子结点】存入vector中。由此可见,时间复杂度为O(n)。

题目2:
0 实验代码及结果
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <iostream>
using namespace std;
typedef struct Node{
char data;//数据域
struct Node *lchild,*rchild;//左孩子结点+右孩子结点
}Node,*BiTree;
char PreString[30],InString[30];//先序和中序遍历字符串 maxsize=30
//根据先序+中序,重新构造原来的树,即BiTree T = new Node();
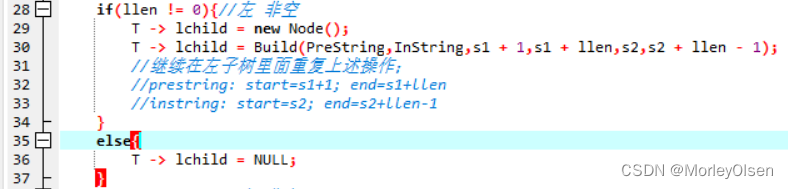
BiTree Build(char *PreString,char *InString,int s1,int e1,int s2,int e2){
//s:start e:end
BiTree T = new Node();
T -> data = PreString[s1];
int rootIdx;//根结点所在序号
for(int i = s2;i <= e2;i++){
if(PreString[s1] == InString[i]){
rootIdx = i;//寻找先序字符串中当前元素在中序字符串中的位置
break;//寻觅结束
}
}
int llen = rootIdx - s2;//左 为 根-初始
int rlen = e2 - rootIdx;//右 为 len(in)-根
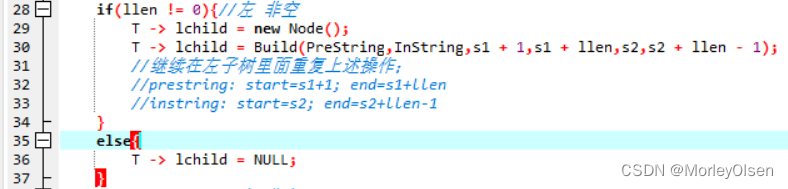
if(llen != 0){//左 非空
T -> lchild = new Node();
T -> lchild = Build(PreString,InString,s1 + 1,s1 + llen,s2,s2 + llen - 1);
//继续在左子树里面重复上述操作;
//prestring: start=s1+1; end=s1+llen
//instring: start=s2; end=s2+llen-1
}
else{
T -> lchild = NULL;
}
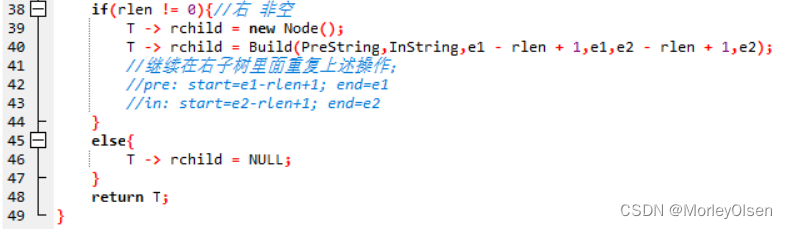
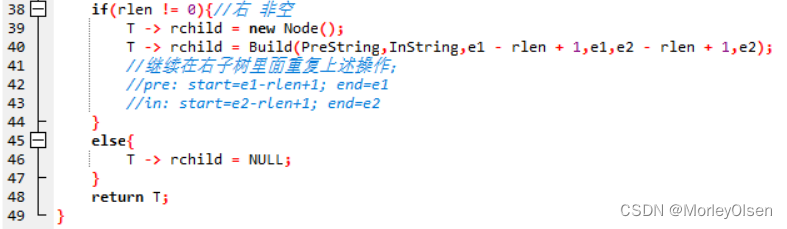
if(rlen != 0){//右 非空
T -> rchild = new Node();
T -> rchild = Build(PreString,InString,e1 - rlen + 1,e1,e2 - rlen + 1,e2);
//继续在右子树里面重复上述操作;
//pre: start=e1-rlen+1; end=e1
//in: start=e2-rlen+1; end=e2
}
else{
T -> rchild = NULL;
}
return T;
}
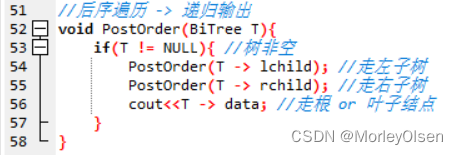
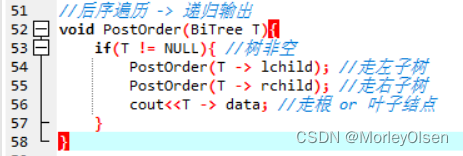
//后序遍历 -> 递归输出
void PostOrder(BiTree T){
if(T != NULL){ //树非空
PostOrder(T -> lchild); //走左子树
PostOrder(T -> rchild); //走右子树
cout<<T -> data; //走根 or 叶子结点
}
}
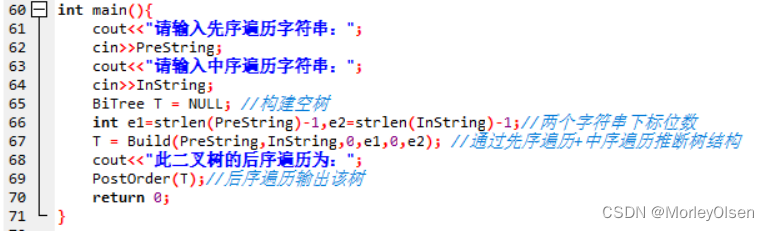
int main(){
cout<<"请输入先序遍历字符串:";
cin>>PreString;
cout<<"请输入中序遍历字符串:";
cin>>InString;
BiTree T = NULL; //构建空树
int e1=strlen(PreString)-1,e2=strlen(InString)-1;//两个字符串下标位数
T = Build(PreString,InString,0,e1,0,e2); //通过先序遍历+中序遍历推断树结构
cout<<"此二叉树的后序遍历为:";
PostOrder(T);//后序遍历输出该树
return 0;
}
题干给的先序遍历+中序遍历构成的二叉树如下图所示:
代码测试结果如下图所示:

1 简述算法步骤
构造一个二叉树,属性携带当前结点数据、当前结点左孩子指针和当前结点右孩子指针。

根据先序遍历【根->左子树->右子树】的特点可知,先序遍历字符串中的第一个结点必然为根,然后通过for循环在中序遍历字符串中寻找与当前结点数据相同的结点,并锁定其在中序遍历字符串中的位置为rootIdx。此时,在中序遍历字符串中,rootIdx左侧的字符串为左子树的内容,rootIdx右侧的字符串为右子树的内容。同时回溯到先序遍历字符串中,可锁定左子树的始末下标和右子树的始末下标。
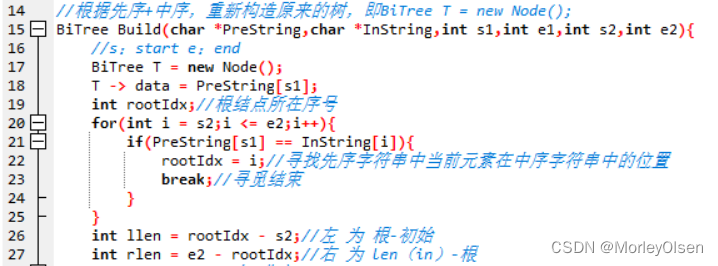
根据树的定义,每一个子树可作为一棵新的树。于是我们将左子树和右子树分别看作新的两个树,确定好新的prestring和instring起始下标之后,重新进行上述操作来确定整个树的空间结构,直至左子树或右子树为空树。最后返回整个树。
在确定整个树的空间结构后,通过递归的后序遍历法【左子树->右子树->根】输出整个树的结点数据。
最后通过主函数依次调用上述算法函数。
2 分析算法时间复杂度
在寻找先序字符串中当前元素在中序字符串中的位置的时候,使用了for循环遍历instring里面的所有结点数据。由此可见,时间复杂度为O(n)。整个递归调用的时间复杂度为O(n logn)。

前俩个递归调用的时候,均通过二分法处理两个遍历字符串,从而进行下一次函数调用。第三个递归调用的时候,也与上述两个递归类似,先通过锁定根结点,分为左子树和右子树继续遍历。由此可见,时间复杂度均为O(n/2)。