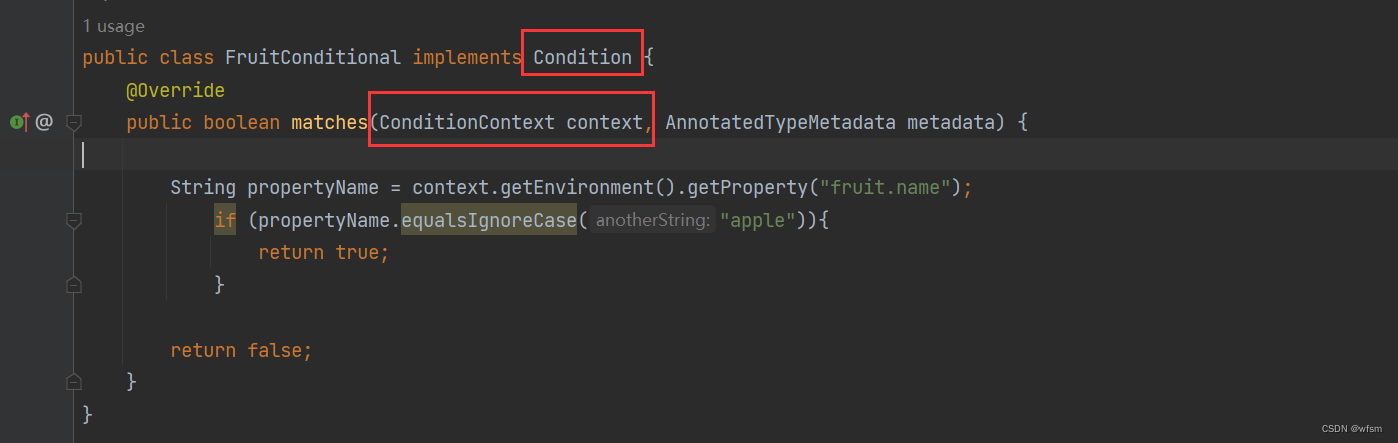
分析一个算法主要看这个算法的执行需要多少机器资源。在各种机器资源中,时间和空间是两个最主要的方面。因此,在进行算法分析时,人们最关心的就是运行算法所要花费的时间和算法中使用的各种数据所占用的空间资源。算法所花费的时间通常称为时间复杂度,使用的空间资源称为空间复杂度。接下来学习如何计算一个算法的时间复杂度和空间复杂度。
1.时间复杂度
在进行算法分析时,语句总的执行次数T(n)是关于问题规模n的函数,然后分析T(n)随n的变化。
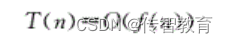
这样用大写的O来标记算法的时间复杂度,称之为大O(Order的简写)标记法。一般随着n的增长,T(n)也会随之增长,其中T(n
)增长最慢者就是时间性能最优的算法。
在计算时间复杂度的时候,根据T(n)与n的最高阶数关系,我们给这些算法的复杂度进行了归类,如表1所示。
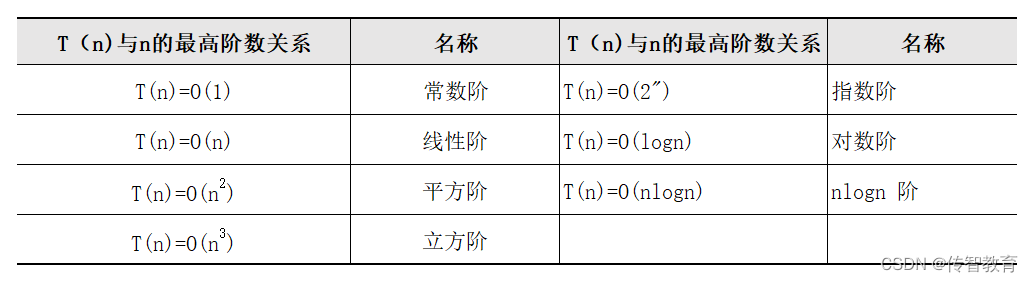
当然还会有一些其他阶数关系,这里只是列出了几种较常见的关系。算法的执行次数可能会与规模n呈现出这些关系,那么这些关系又是如何推导出来的呢?下面给出大O阶的推导方法:
(1)用常数1取代运行中的所有加法常数。
(2)在修改后的运行次数函数中,只保留最高阶项。
(3)如果最高阶项存在,且不是1,则除去其常系数,得到的结果就是大O阶。
接下来通过分析几段程序的执行过程来推导出其时间复杂度,程序段1代码如下所示:
int a=100; //执行一次
int b=200; //执行一次
int sum=a+b; //执行一次
printf("&d\n",sum); //执行一次
上述程序段有4行代码,每一行执行1次,加起来一共执行了4次,f(n)=4,即T(n)=O(4)。根据推导方法中的第一条,将常数项以1代替。在保留其最高阶项时,发现其没有最高阶项,因此该算法的时间复杂度为O(1),为常数阶。程序段2代码如下所示:
void func()
{
int i,sum=0; //执行一次
for (i=0;i<=100;i++)
{
sum +=i; //执行n次
}
printf("sd\n",sum); //执行一次
}
该程序段的执行次数为1+n+1,则f(n)=n+2,即T(n)=O(n+2)。然后将常数项以1替换,且只保留最高阶项,则得出T(n)=O(n),因此该算法的时间复杂度为O(n),为线性阶。
程序段3代码如下所示:
void func()
{
int i=l;
do
{
i*=2;
}
while (i<n);
}
在这个程序段中,当i<n时,循环结束。如果循环了f(n)次,则2(fn)=n,即f(n)=log2n,T(n)=O(log2n)。然后消除常系数,保留最高阶项,最后得出T(n)=O(logn),为对数阶。
用大O阶来推导算法的复杂度并不难,读者在以后的学习中设计算法,就可以用此法来估测算法的优劣。
2.空间复杂度
空间复杂度是对一个算法在运行过程中所占存储空间大小的度量,一般也作为问题规模n的函数,以数量级形式给出,格式如下所示:

一个算法的存储量包括输入数据所占空间、程序本身所占空间和辅助变量所占空间。在对算法进行分析时,只考虑辅助变量所占空间。若所需辅助空间相对于输入数据量来说是常数,则称此算法为原地工作。若所用空间量依赖于特定的输入,则除了有特殊说明外,均按最坏情况考虑。
有时候,在写代码时可以用空间来换取时间,例如,写一个算法来判断某年是否是闰年,这样每输入一个年份都要调用算法去判断一下,在时间上就有点复杂。为了提高效率,可以用空间来换取时间,即建立一个大小合适的数据,编号从0到n,如果是闰年,则存入数据1,否则存入数据0。这样只要通过判断年份编号上存储的是0还是1就知道该年份是否是闰年了。
用空间换取时间可以将运算最小化,但这两种情况哪种更好,要结合具体情况而定。一般情况下,都是用时间复杂度来度量算法,当不加限定地使用“复杂度”这一术语时,都是指时间复杂度。