数据准备

我们首先需要加载波士顿房价数据集。该数据集包含房屋特征信息和对应的房价标签。

import pandas as pd
import numpy as np

data_url = "http://lib.stat.cmu.edu/datasets/boston"
raw_df = pd.read_csv(data_url, sep="\s+", skiprows=22, header=None)
data = np.hstack([raw_df.values[::2, :], raw_df.values[1::2, :2]])
target = raw_df.values[1::2, 2]

print("数据集大小：{}".format(data.shape))
print("标签大小：{}".format(target.shape))

数据划分

接下来，我们将数据集划分为训练集和测试集。

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(data, target, random_state=8)

正规方程方法

正规方程是线性回归问题的闭式解，它直接计算参数的最优解而无需迭代。我们使用 LinearRegression 类来训练模型，并输出训练集和测试集上的得分、参数和截距。

from sklearn.linear_model import LinearRegression

lr = LinearRegression()
lr.fit(X_train, y_train)

print("正规方程训练集得分：{:.3f}".format(lr.score(X_train, y_train)))
print("正规方程测试集得分：{:.3f}".format(lr.score(X_test, y_test)))
print("正规方程参数：{}".format(lr.coef_))
print("正规方程截距：{:.3f}".format(lr.intercept_))

模型评估

我们使用均方误差和均方根误差来评估模型的性能。

from sklearn.metrics import mean_squared_error

y_pred = lr.predict(X_test)

print("正规方程均方误差：{:.3f}".format(mean_squared_error(y_test, y_pred)))
print("正规方程均方根误差：{:.3f}".format(np.sqrt(mean_squared_error(y_test, y_pred))))

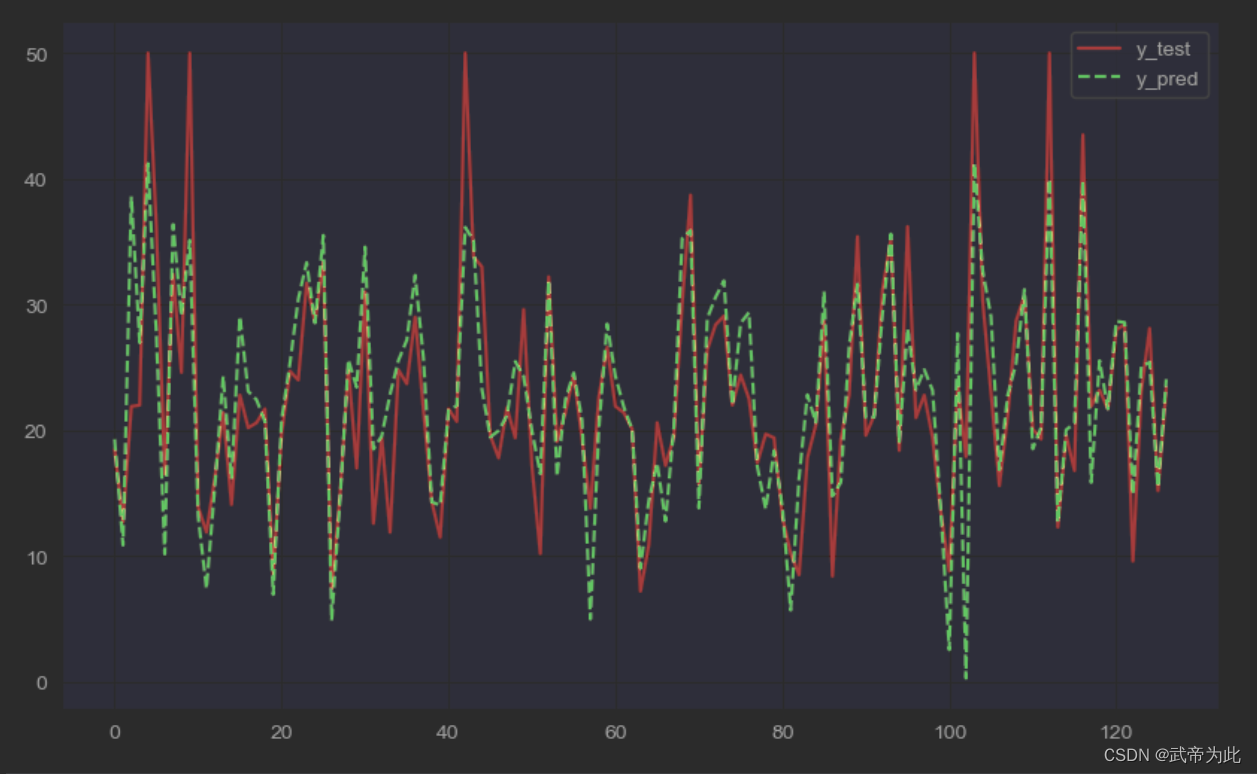
可视化

最后，我们将真实值和预测值进行可视化比较，以便更直观地了解模型的拟合效果。

import matplotlib.pyplot as plt

plt.figure(figsize=(10, 6))
plt.plot(range(len(y_test)), y_test, "r", label="y_test")
plt.plot(range(len(y_pred)), y_pred, "g--", label="y_pred")
plt.legend()
plt.show()