239. 滑动窗口最大值
目录
239. 滑动窗口最大值
347. 前 K 个高频元素
239. 滑动窗口最大值
难度:hard
类型:队列,单调队列,滑动窗口

思路:
构造单调队列,维护大小为k的队列。队列里的元素始终是单调递减的,处于队列出口的元素始终是最大值。使用Deque来维护这个单调队列。
代码:
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
int len = nums.length;
if (len == 1) {
return nums;
}
// 存储答案的数组,有len-k+1个窗口,每个窗口一个最大值
int[] ans = new int[len - k + 1];
// ans数组的计数
int num = 0;
// 声明单调队列
MyQueue queue = new MyQueue();
// 先将第一个窗口的k个元素添加进去
for (int i = 0; i < k; i++) {
queue.push(nums[i]);
}
ans[num++] = queue.getMaxValue();
for (int i = k; i < len; i++) {
// pop出窗口中最左边的元素
queue.pop(nums[i - k]);
queue.push(nums[i]);
ans[num++] = queue.getMaxValue();
}
return ans;
}
}
// 单调队列
class MyQueue {
// 双端队列维护单调队列
public Deque<Integer> deque = new LinkedList<>();
// 添加元素时,如果要添加的元素大于入口处的元素,就将入口元素弹出
// 保证队列元素单调递减
// 比如此时队列元素3,1,2将要入队,比1大,所以1弹出,此时队列:3,2
public void push(int val) {
while (!deque.isEmpty() && deque.peekLast() < val) {
deque.pollLast();
}
deque.offerLast(val);
}
// 判断窗口左端元素是否是队列的左出口元素,若是则pop;反之则说明窗口左端元素已经被pop了
public void pop(int val) {
if (!deque.isEmpty() && val == deque.peekFirst()) {
deque.pollFirst();
}
}
// 队列里的前出口元素即为队列里的最大值
public int getMaxValue() {
return deque.peekFirst();
}
}复杂度分析:
- 时间复杂度: O(n)
- 空间复杂度: O(k)
347. 前 K 个高频元素
难度:medium
类型:堆,优先队列
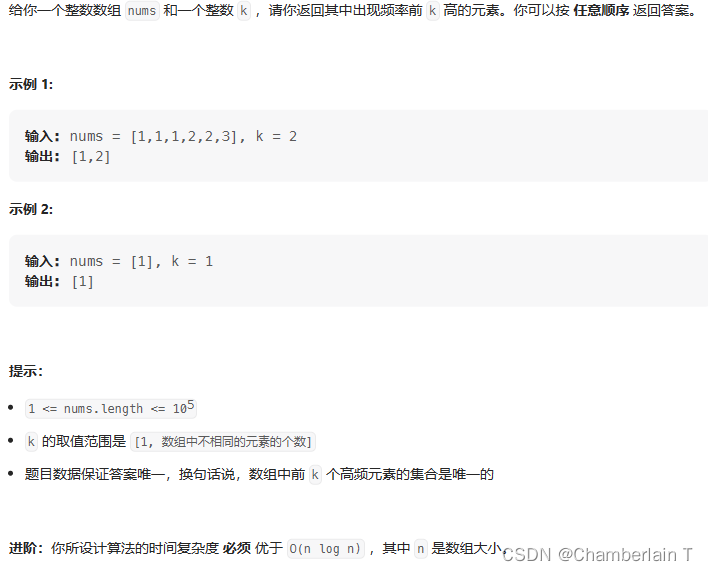
思路:
参考文章:(51条消息) LeetCode.347. 前 K 个高频元素_Chamberlain T的博客-CSDN博客
代码随想录 (programmercarl.com)
需要掌握PriorityQueue优先队列和Map.Entry键值对;
小顶堆的方法是符合时间复杂度优于O(nlogn)的,因为小顶堆方法只需要维持k个最大元素,所以其时间复杂度为O(nlogk).
利用hashmap来记录数组中的元素和对应的出现次数,用优先队列来找出频率最高的k个元素。
代码:
// 基于大顶堆实现
class Solution {
public int[] topKFrequent(int[] nums, int k) {
Map<Integer, Integer> map = new HashMap<>();
for (int num: nums) {
map.put(num, map.getOrDefault(num, 0) + 1);
}
// 构造大顶堆(o2-o1),直接存储Entry键值对
PriorityQueue<Map.Entry<Integer, Integer>> pd = new PriorityQueue<>((o1, o2) -> o2.getValue() - o1.getValue());
// 将map中存储的键值对放入优先队列中
for (Map.Entry<Integer, Integer> entry: map.entrySet()) {
pd.offer(entry);
}
int[] ans = new int[k];
for (int i = 0; i < k; i++) {
ans[i] = pd.poll().getKey();
}
return ans;
}
}
// 基于小顶堆实现
// 时间复杂度O(nlogk),空间复杂度O(n);因为只需要维持大小为k的小顶堆
class Solution {
public int[] topKFrequent(int[] nums, int k) {
Map<Integer, Integer> map = new HashMap<>();
for (int num: nums) {
map.put(num, map.getOrDefault(num, 0) + 1);
}
PriorityQueue<int[]> pd = new PriorityQueue<>((o1, o2) -> o1[1] - o2[1]);
for (Map.Entry<Integer, Integer> entry: map.entrySet()) {
if (pd.size() < k) {
pd.offer(new int[]{entry.getKey(), entry.getValue()});
} else {
// 优先队列元素个数超出k个,把最小的元素弹出:比较新元素的小顶堆堆顶元素
if (entry.getValue() > pd.peek()[1]) {
pd.poll();
pd.offer(new int[]{entry.getKey(), entry.getValue()});
}
}
}
int[] ans = new int[k];
for (int i = 0; i < k; i++) {
ans[i] = pd.poll()[0];
}
return ans;
}
}复杂度分析:
大顶堆方法:时间复杂度O(nlogn),空间复杂度O(n)
小顶堆方法:时间复杂度O(nlogk),空间复杂度O(n);因为只需要维持大小为k的小顶堆