0 知识回顾

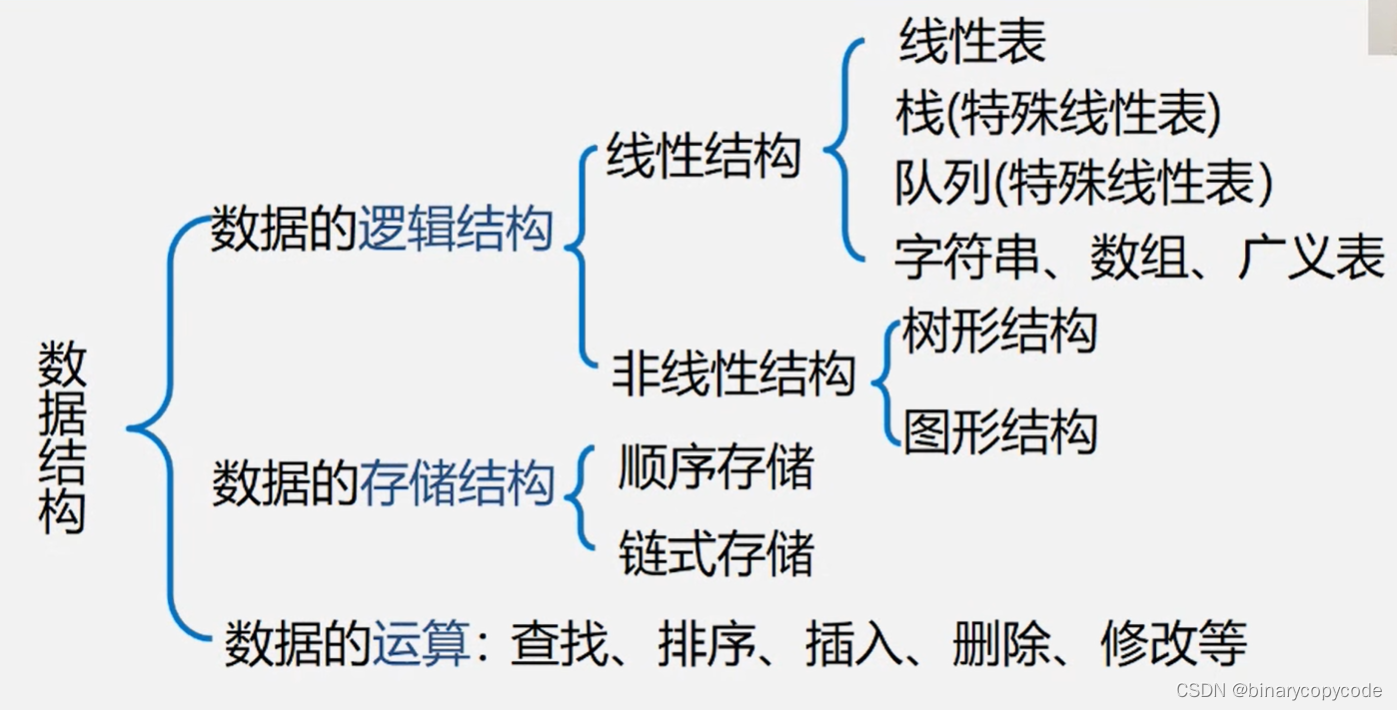
1 查找

1.1 查找的概念

Q: 查找是在哪里找？
A :查找表，查找表没有前驱以及后继的关系。
查找表是由同一类型的数据元素（或记录）构成的集合。由于“集合”中的数据元素之间存在着松散的关系，因此查找表是一种应用灵便的结构。

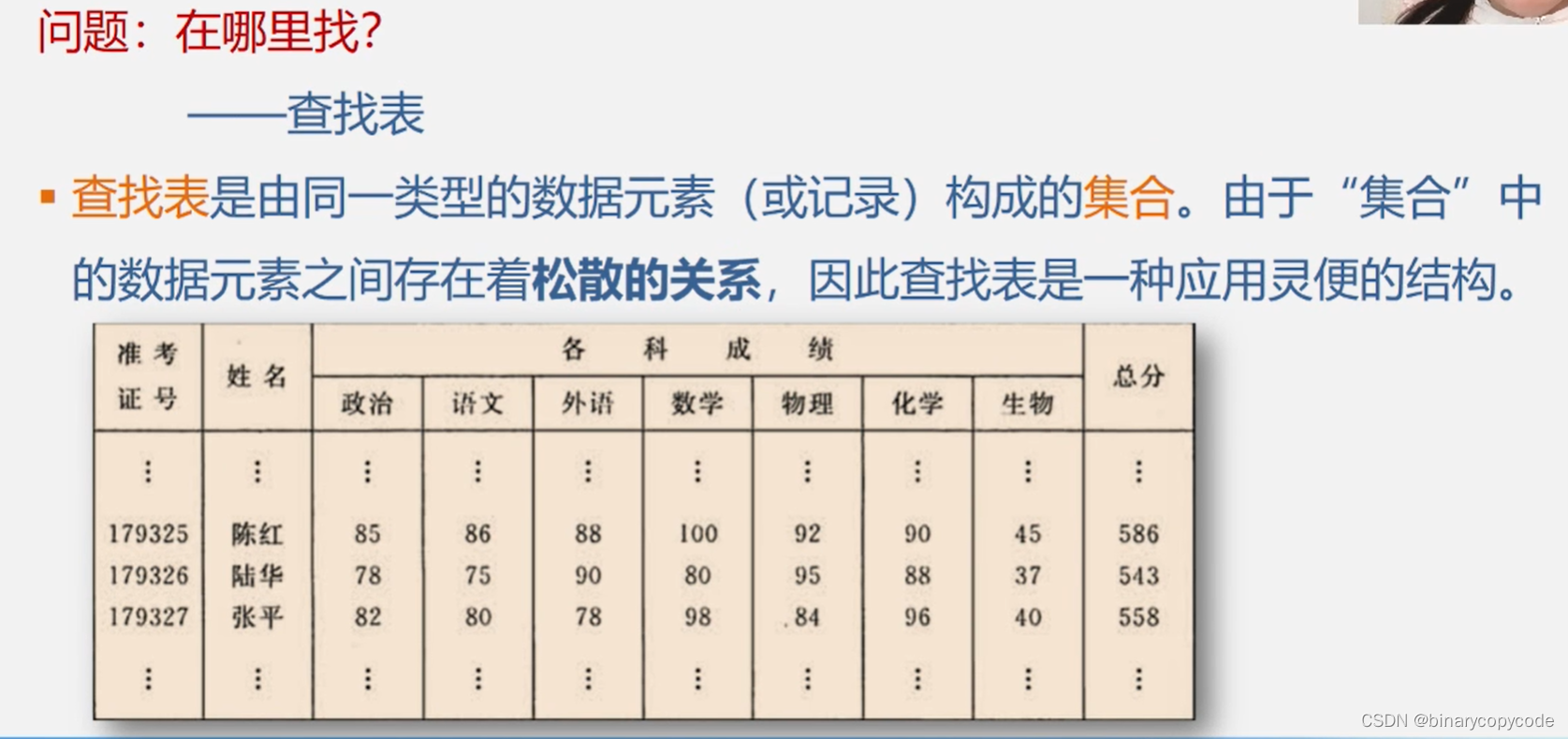
Q:怎么查找？
A:根据给定的某个值，在查找表中确定一个其关键字等于给定值的数据元素或（记录）。

关键字，即用来标识一个数据元素（或记录）的某个数据项的值，有以下几类关键字：

• 主关键字：可唯一地标识一个记录的关键字是主关键字；
• 次关键字：反之，用以识别若干记录的关键字是次关键字。

以下为判断查找是否成功

以下为看查找的目的

以下为查找的分类

以下评价查找算法的性能分析

以下为查找研究的是什么？

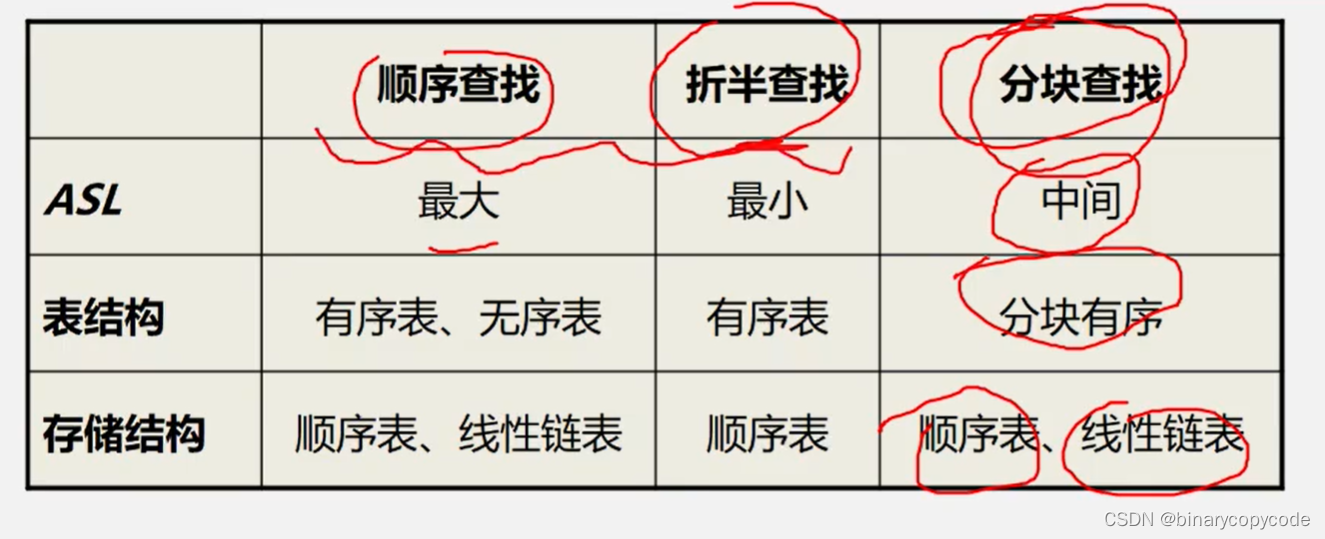
2 线性表的查找

线性表的查找有以下几种方式：

1. 顺序查找
2. 折半查找（二分或者对分查找）
3. 分块查找

2.1 顺序查找

//数据元素类型定义
typedef struct
{
	KeyType key;//关键字域
	......//其他域
}ElemType;
//
typedef struct
{
	ElemType *R; //表基址
	int length; //表长
}SSTable; //Sequential Search Table
SSTable ST;//定义顺序表

2.1.1 顺序查找算法

算法的其他形式：


问题： 每执行一次循环都要进行两次比较是否能改进？
改进： 把待查关键key存入表头（“俏兵”、”监视哨”)，从一后往前逐个比较，可免去查找过程中每一步都变检测是否查我完毕，从而加快速度。

设置监事岗的，就只需要比较1次。

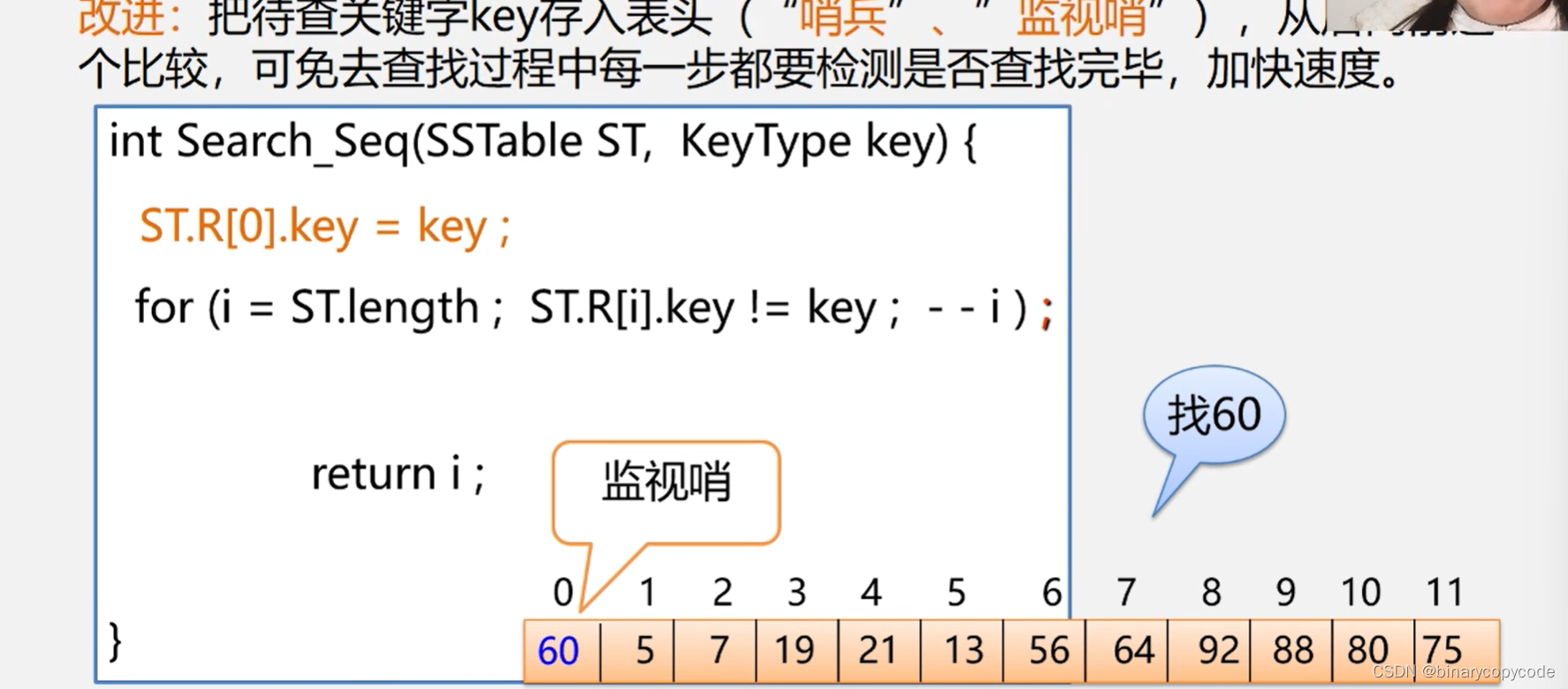
最终算法：

当ST.length()较大时，此改进能使进行一次查找所需的平均时间几乎减少一半。注意此时的for循环是空语句，然后直接返回i的下标就行。

比较次数与key位置有关：

• 查找第个元素，需要比较n-i+1次
• 查找失败，需比较n+1次（开始的时候就把要查找的值存入起始节点当做哨兵，所以查找失败就从最后一个往回退，即查找n+1次）

2.1.2 顺序查找的性能分析

顺序查找的性能：

• 时间复杂度：$O(n)$，查找成功时的平均查找长度，设表中的各记录查找概率相等。
  $AS{L}_s(n)=(1+2+...+n)/n=(n+1)/2$
• 空间复杂度：一个辅助空间（哨兵）—$O(1)$
  

2.1.3 顺序查找的特点

• 优点：算法简单，逻辑次序无要求，且不同存储结构均适用。
• 缺点：ASL太长时间效率太低。

2.2 折半查找（二分）

就是先排序，排序好后先判断，从中间判断，判断所要找的数与中间的数的大小，所要找的数比中间的数大，则low = mid + 1，只找右半边；所要找的数比中间的数小，则high = mid - 1，只找左半边。结束的条件为high < low。关于mid除下来不是整数，可以使用取整的符号。

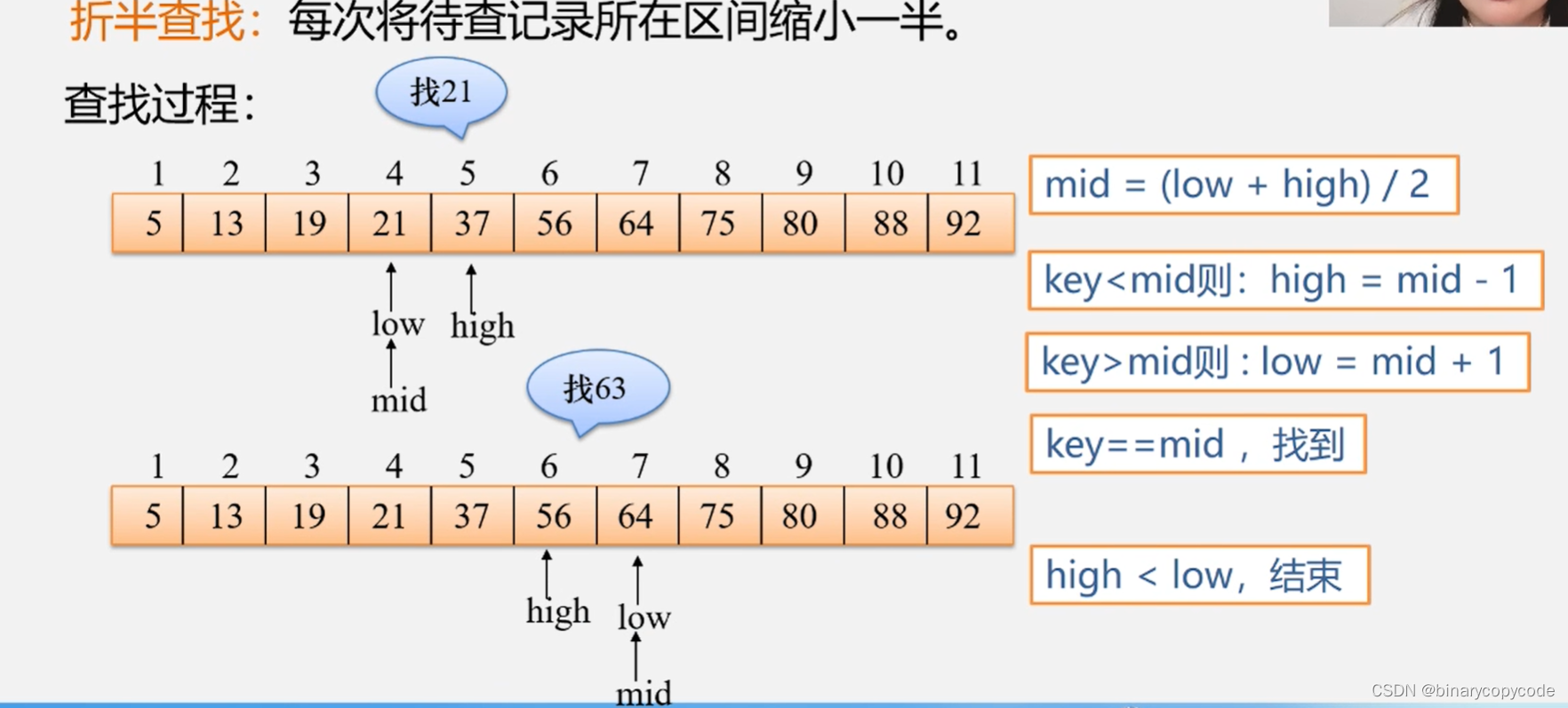
2.2.1 折半查找算法

非递归实现的形式：

int Search_Binary(SSTable ST, KeyType key)
{
	low = 1;
	high = ST.length();//区间初值
	while (low <= high)
	{
		mid = (low + high) / 2;
		if (ST.R[mid].key == key)
		{
			return mid;//找到待查元素
		}
		else if (key < ST.R[mid].key) //缩小查找区间
		{
			high = mid - 1; //继续在前半区间进行查找
		}
		else
		{
			low = mid + 1; //继续在后半区间进行查找
		}
	}
	return 0; //顺序表中不存在待查元素
}

递归实现的形式：

int Search_Binary(SSTable ST, keyType key, int low, int high)
{
	if (low > high)
	{
		return 0;//查找不到返回0
	}
	mid = (low + high) / 2;
	if (key == ST.elem[mid].key)
	{
		return mid;
	}
	else if (key < ST.elem[mid].key)//递归，在前半区间进行查找
	{
		Search_Binary(ST, key, low, mid-1);
	}
	else//递归，在后半区间进行查找
	{
		Search_Binary(ST, key, mid+1, high);
	}
}

2.2.2 折半查找的性能分析

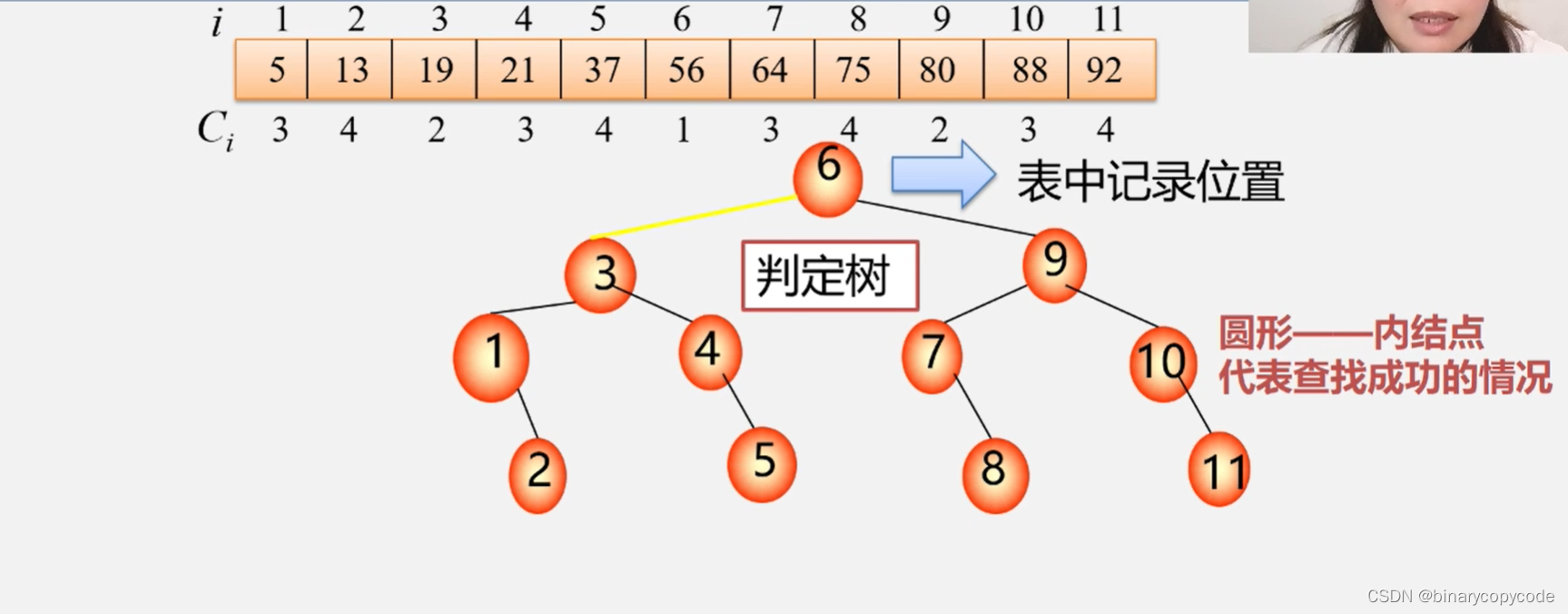
折半查找的时间复杂度为$O(logn)$

2.2.3 折半查找的特点

• 折半查找优点：效率比顺序查找高
• 折半查找缺点：只适用有序表，且限于顺序存储结构（对线性链表无效）

2.3 分块查找

按照索引顺序表进行查找。

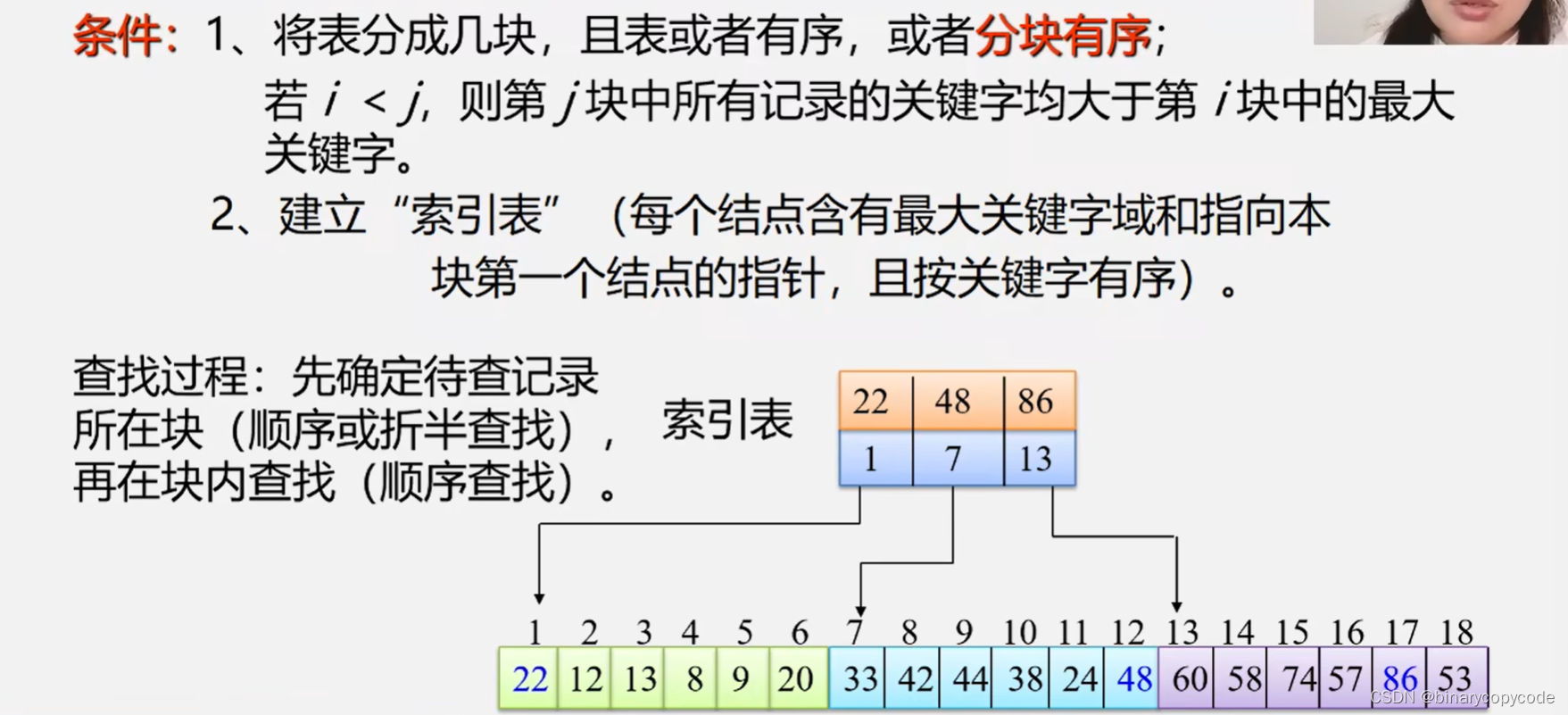
2.3.1 分块查找的性能分析

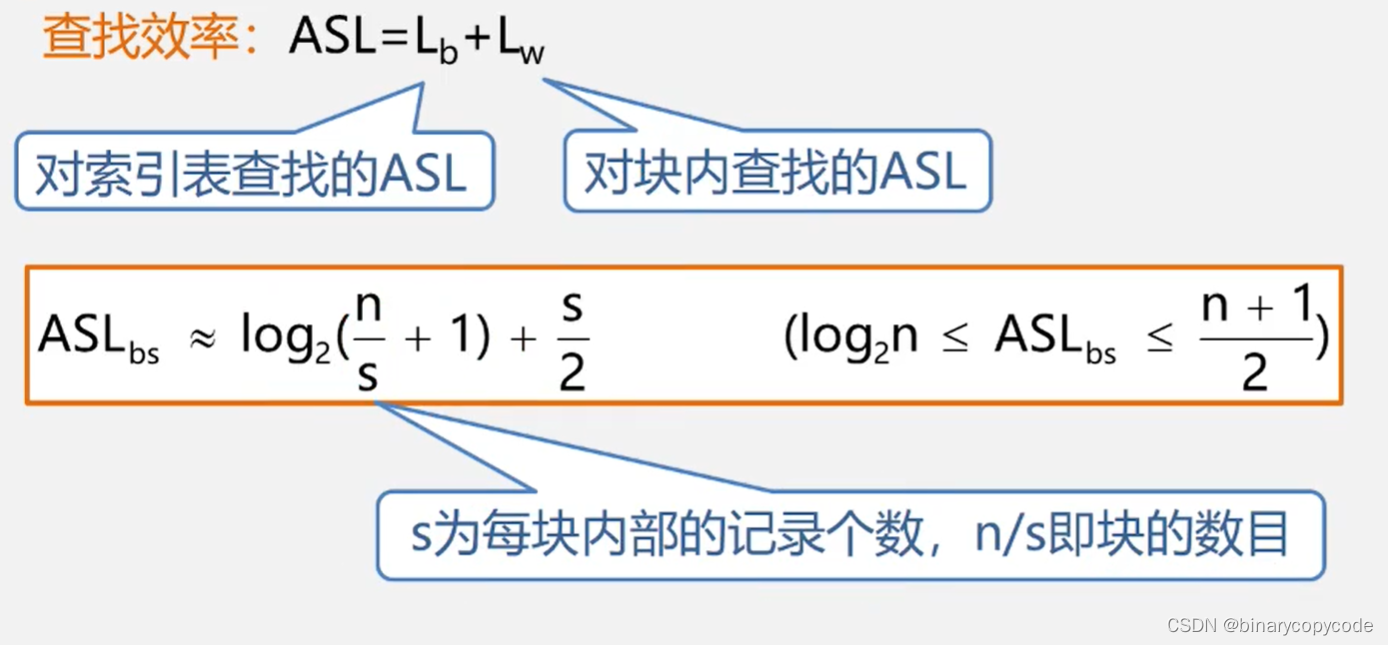
插入删除比较方便。

2.3.2 分块查找的特点

• 优点：插入和删除比较容易，无需进行大量移动。
• 缺点：要增加一个索引表的存储空间并对初始索引表进行排序运算。
• 适用情况：如果线性表既要快速查找又经常动态变化，则可采用分块查找。