12. 背包问题求具体方案 - AcWing题库

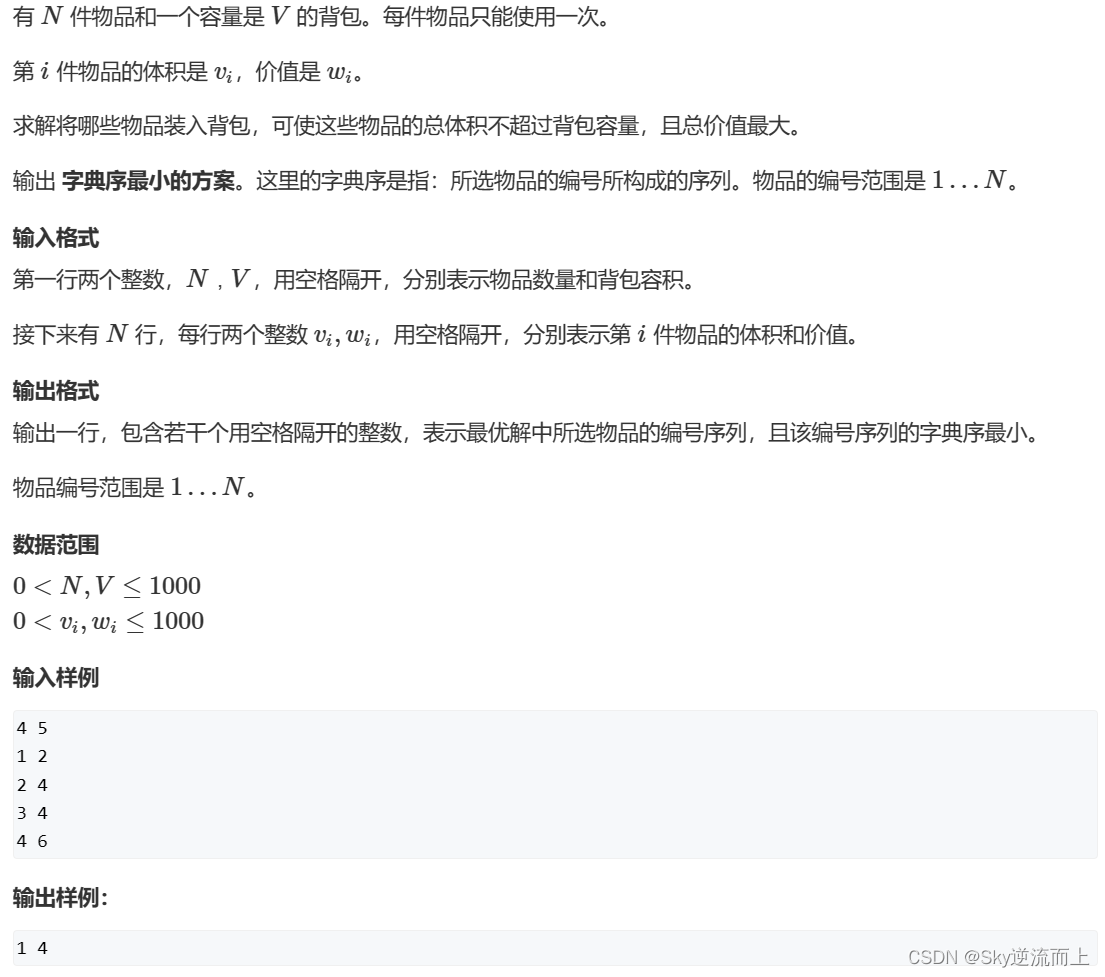
 思路：先将v[i]和w[i]先输入进去，然后我们进行倒叙dp，这个做的目的就是为了后边我们为了匹配确定路径做好准备，如果我们倒叙输入进去，我们再正序的时候就可以用推导式来进行路径输出

 这个题如果简单的看作的背包问题是非常简单的,状态转移方程就是:f[i][j]=max(f[i-1][j],f[i-1][j-v[i]+w[i])，通过刚才的倒叙：f[i][j]=max(f[i+1][j],f[i+1][j-v[i]+w[i])

所以我们到时候判断路径的时候只需要取判断是否为f[i][j]==f[i+1][j-v[i]]+w[i],就可以确定这个路径是否在我们的最短路径之中，输出即可。

#include<bits/stdc++.h>
using namespace std;
const int N=2e5+100;
int v[N];
int w[N];
int f[1010][1010];
int main()
{
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    {
        cin>>v[i]>>w[i];
    }
    for(int i=n;i>=1;i--)
    {
        for(int j=0;j<=m;j++)
        {
            f[i][j]=f[i+1][j];
            if(j>=v[i]) f[i][j]=max(f[i][j],f[i+1][j-v[i]]+w[i]);
        }
    }
    int j=m;
    for(int i=1;i<=n;i++)
    {
        if(j>=v[i]&&f[i][j]==f[i+1][j-v[i]]+w[i])
        {
            cout<<i<<" ";
            j-=v[i];
        }
    }
    return 0;
}