💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
📚2 运行结果
2.1 算例1
2.2 算例2
2.3 算例3
🎉3 参考文献
🌈4 Matlab代码实现
💥1 概述
变分模态分解(VMD)是近年来引入的一种自适应数据分析方法,在各个领域引起了广泛的关注。然而,VMD是基于信号模型窄带特性的假设而制定的。为了分析宽带非线性线性调频信号(NCS),我们提出了一种称为变分非线性线性调频模式分解(VNCMD)的替代方法。VNCMD的开发基于这样一个事实,即宽带NCS可以通过使用解调技术转换为窄带信号。因此,我们的分解问题被表述为最优解调问题,通过乘法的交替方向方法(ADMM)有效地求解。我们的方法可以看作是一个时频(TF)滤波器组,它同时提取所有信号模式。提供了一些模拟和真实的数据示例,展示了VNCMD在分析包含接近甚至交叉模式的NCS方面的有效性。
📚2 运行结果
2.1 算例1

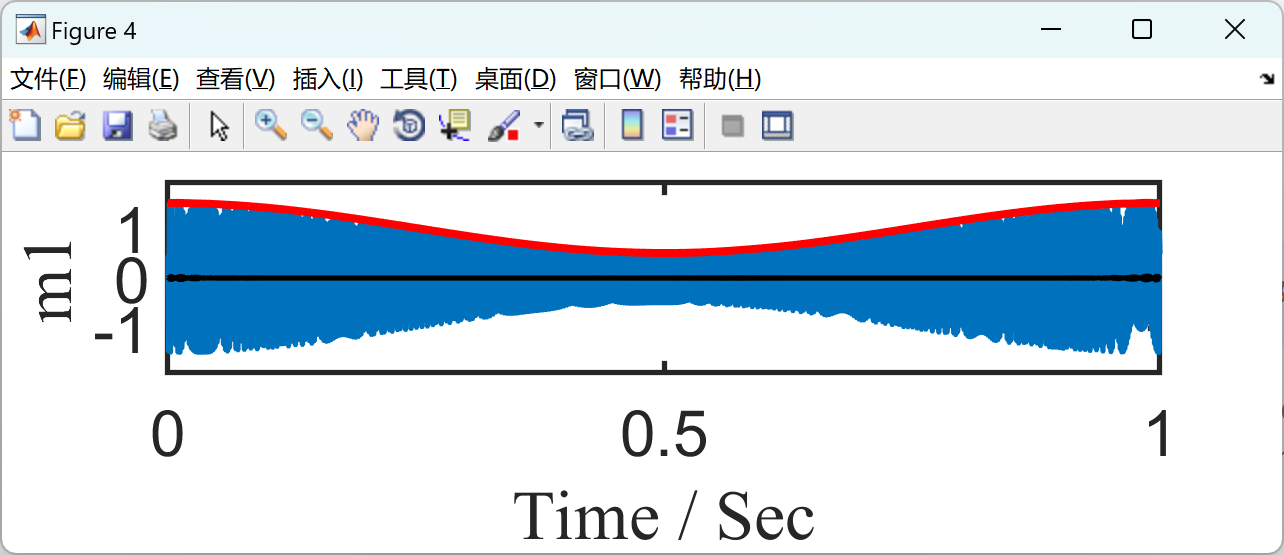
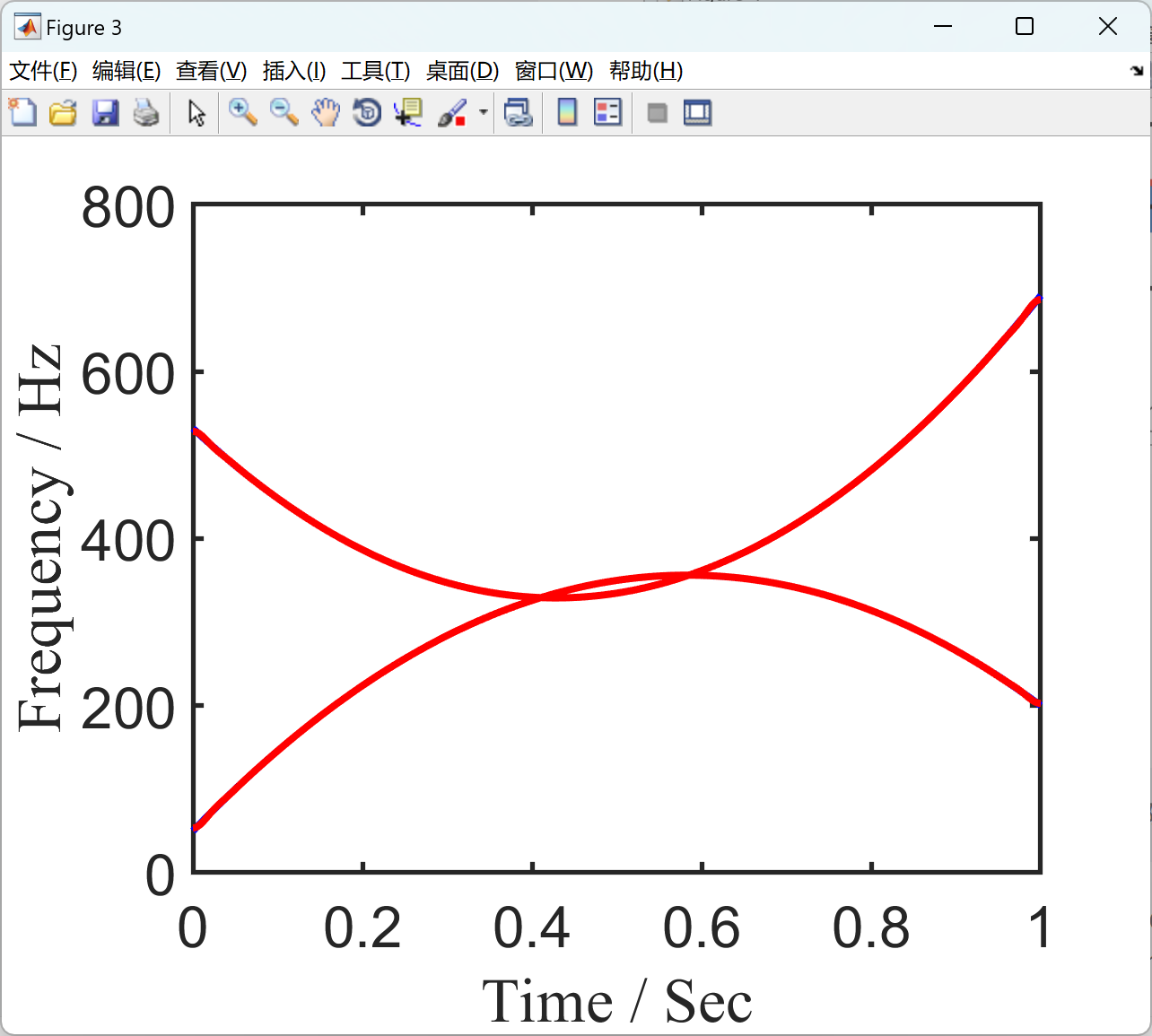
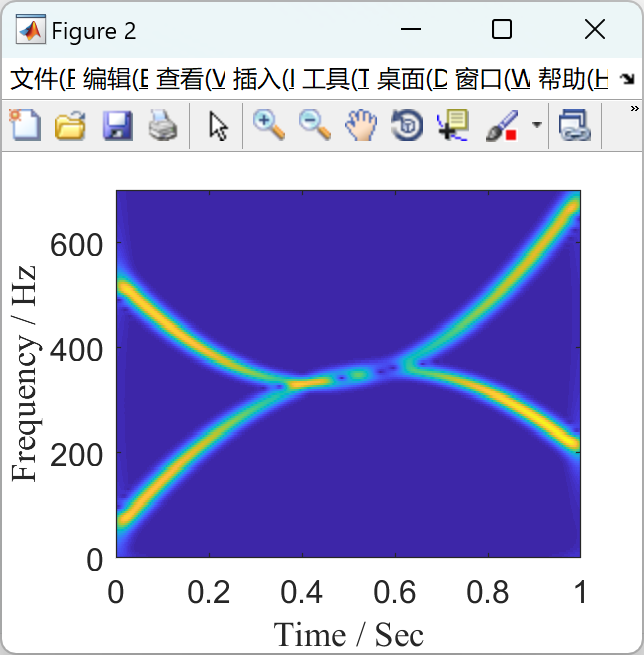
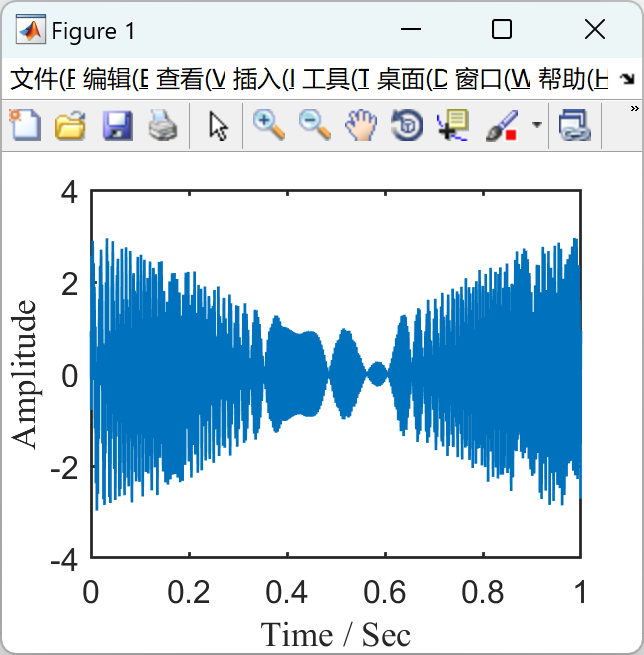
2.2 算例2
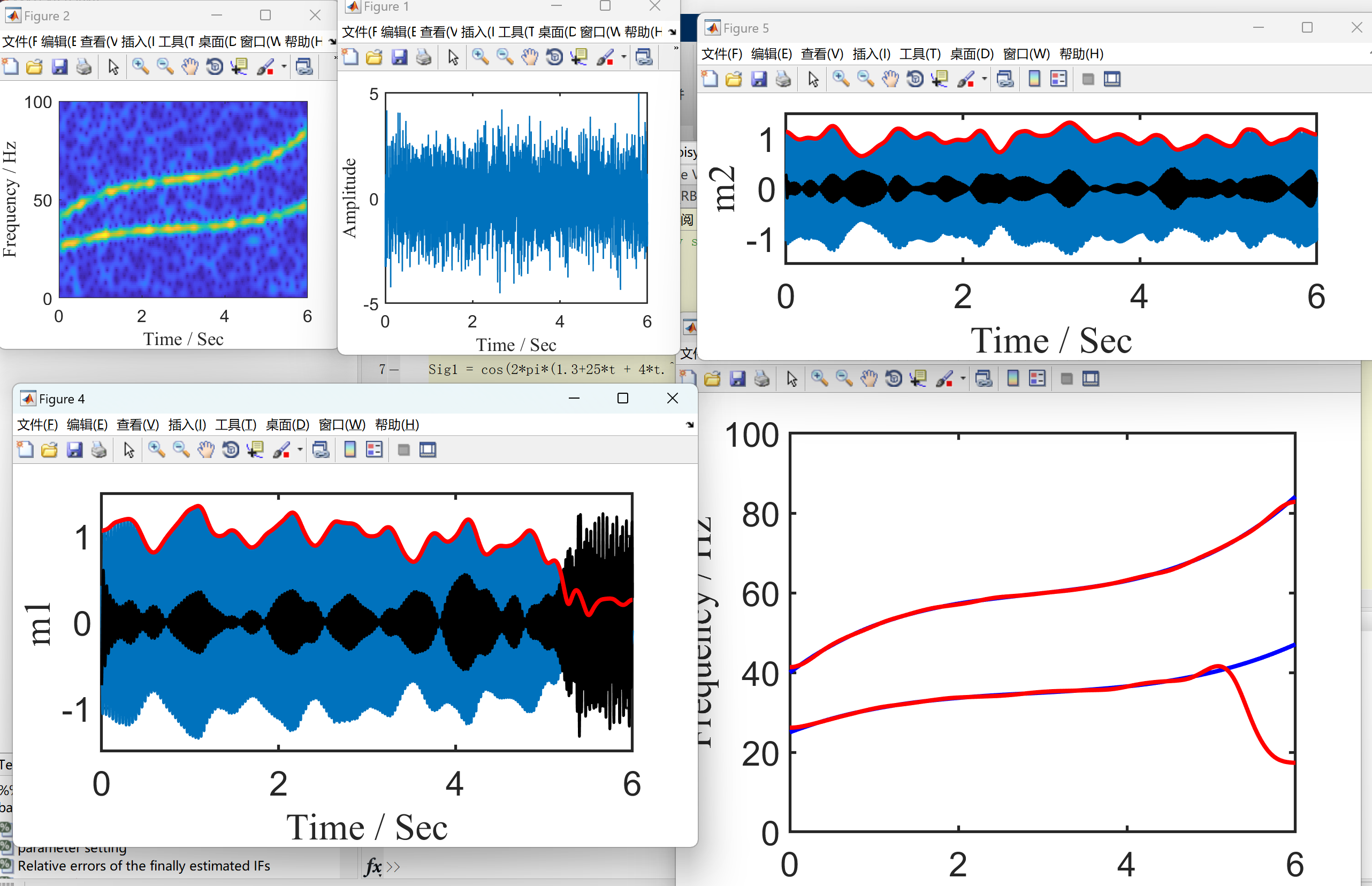
2.3 算例3
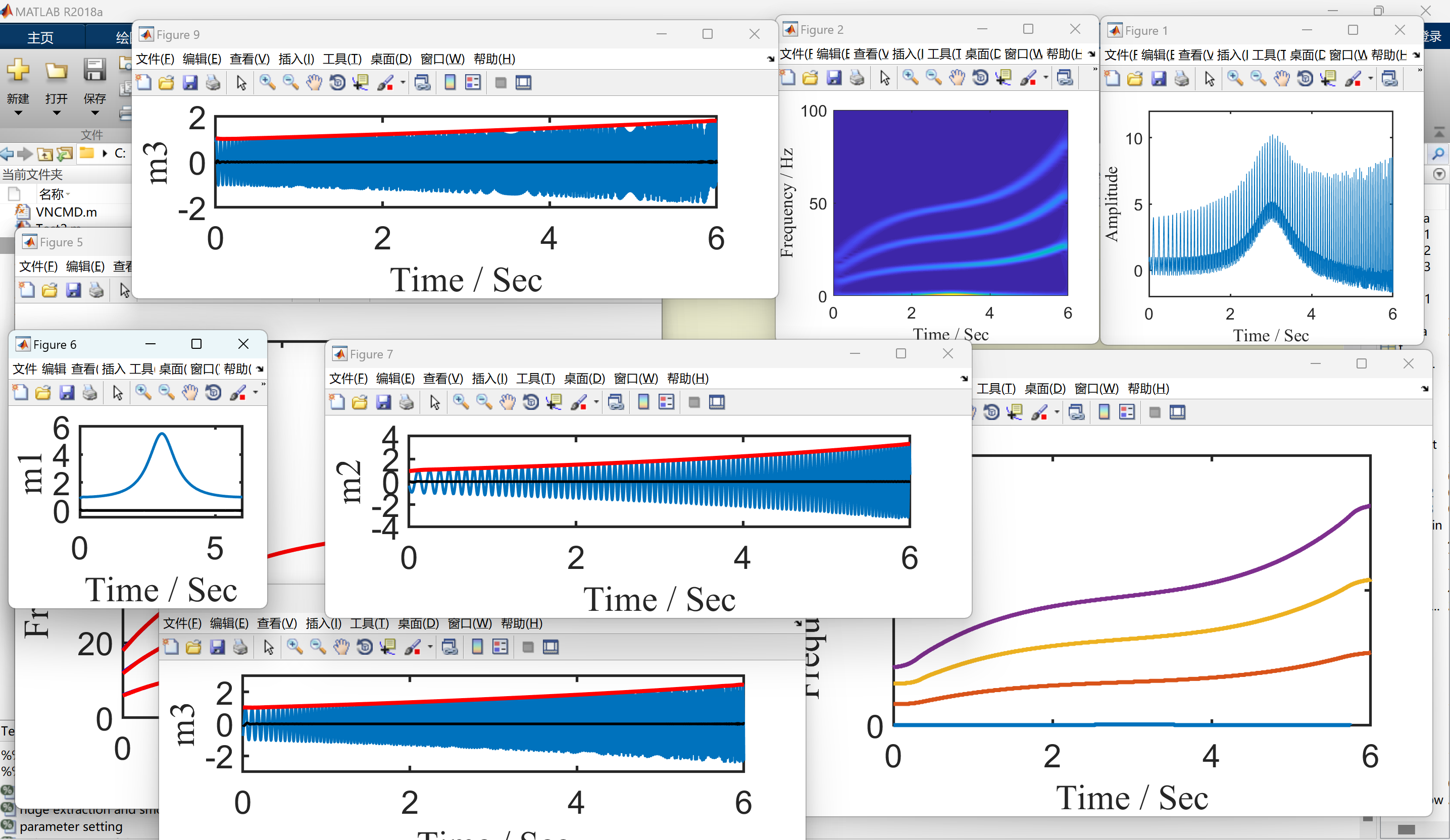
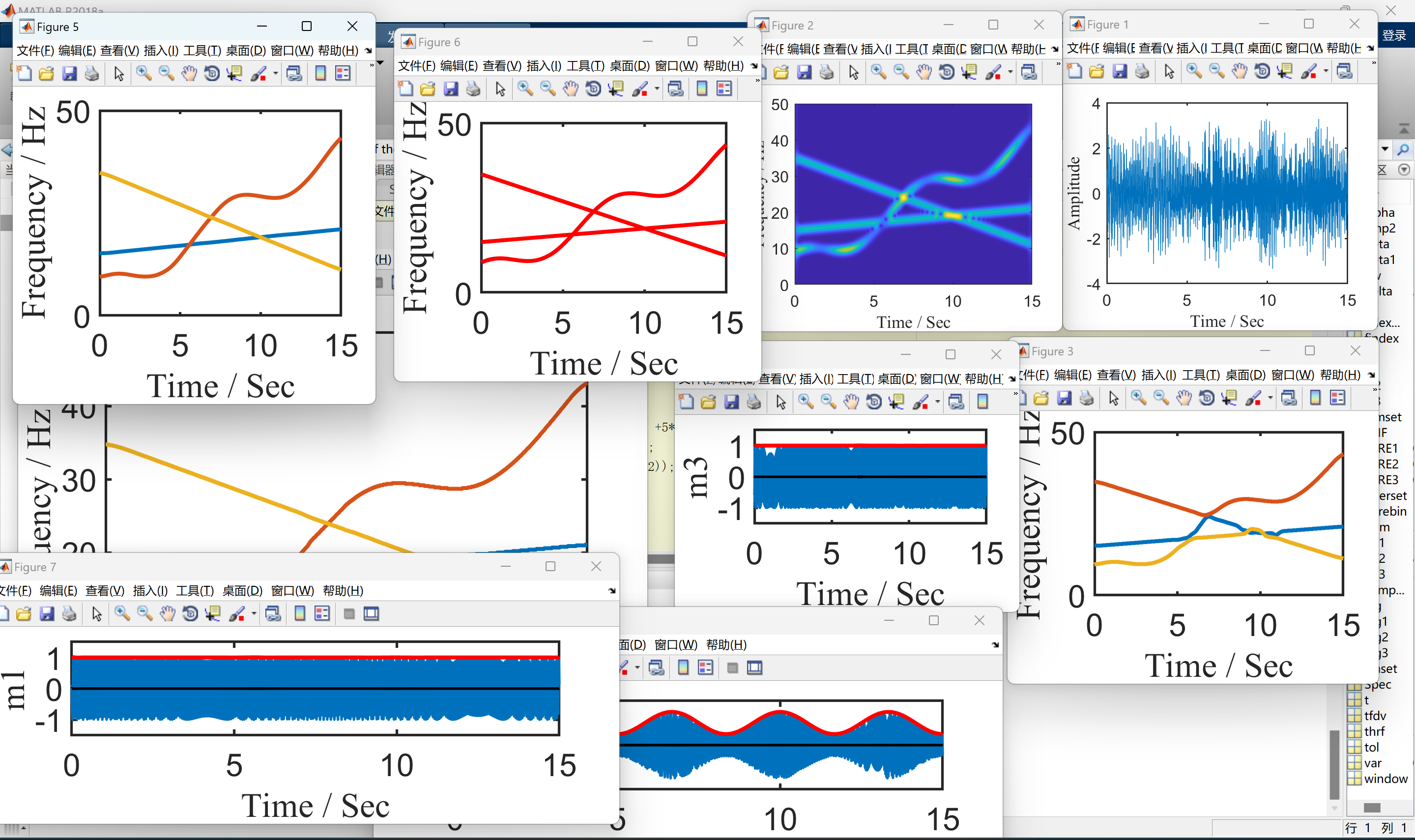
部分代码:
%% initialize
[K,N] = size(eIF);%K is the number of the components,N is thenumber of the samples
t = (0:N-1)/fs;%time
e = ones(N,1);
e2 = -2*e;
% e2(1) = -1;e2(end) = -1;
oper = spdiags([e e2 e], 0:2, N-2, N);% oper = spdiags([e e2 e], -1:1, N, N);%the modified second-order difference matrix
opedoub = oper'*oper;%
sinm = zeros(K,N);cosm = zeros(K,N);%
xm = zeros(K,N);ym = zeros(K,N);%denote the two demodulated quadrature signals
iternum = 300; %the maximum allowable iterations
IFsetiter = zeros(K,N,iternum+1); IFsetiter(:,:,1) = eIF; %the collection of the obtained IF time series of all the signal modes at each iteration
ssetiter = zeros(K,N,iternum+1); %the collection of the obtained signal modes at each iteration
lamuda = zeros(1,N);%Lagrangian multiplier
for i = 1:K
sinm(i,:) = sin(2*pi*(cumtrapz(t,eIF(i,:))));
cosm(i,:) = cos(2*pi*(cumtrapz(t,eIF(i,:))));
Bm = spdiags(sinm(i,:)', 0, N, N);Bdoubm = spdiags((sinm(i,:).^2)', 0, N, N);%Bdoubm = Bm'*Bm
Am = spdiags(cosm(i,:)', 0, N, N);Adoubm = spdiags((cosm(i,:).^2)', 0, N, N);%Adoubm = Am'*Am
xm(i,:) = (2/alpha*opedoub + Adoubm)\(Am'*s(:));
ym(i,:) = (2/alpha*opedoub + Bdoubm)\(Bm'*s(:));
ssetiter(i,:,1) = xm(i,:).*cosm(i,:) + ym(i,:).*sinm(i,:);%
end
%% iterations
iter = 1;% iteration counter
sDif = tol + 1;%
sum_x = sum(xm.*cosm,1);%cumulative sum
sum_y = sum(ym.*sinm,1);%cumulative sum
while ( sDif > tol && iter <= iternum ) %
betathr = 10^(iter/36-10);%gradually increase the parameter beta during the iterations
if betathr>beta
betathr = beta;
end
u = projec(s - sum_x - sum_y - lamuda/alpha,var);%projection operation; u denotes the noise variable; if let var=0, the output u will be zeros.
%%%%%%%%%%%%%%%%%%%%%%%%%%%% update each mode %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
for i = 1:K
% lamuda = zeros(1,N);% if one wants to drop the Lagrangian multiplier, just set it to zeros, i.e., delete the first symbol % in this line.
%%%%%%%%%%%%% update the two matrices A and B %%%%%%%%%%%%%%%%%%%%%%%%%%%
Bm = spdiags(sinm(i,:)', 0, N, N);Bdoubm = spdiags((sinm(i,:).^2)', 0, N, N);
Am = spdiags(cosm(i,:)', 0, N, N);Adoubm = spdiags((cosm(i,:).^2)', 0, N, N);
%%%%%%%%%%%%% x-update %%%%%%%%%%%%%%%%%%%%%%%%%%%
sum_x = sum_x - xm(i,:).*cosm(i,:);% remove the relevant component from the sum
xm(i,:) = (2/alpha*opedoub + Adoubm)\(Am'* (s - sum_x - sum_y - u - lamuda/alpha)');%
interx = xm(i,:).*cosm(i,:);% temp variable
sum_x = sum_x + interx;% update the sum
%%%%%%%%%%%%% y-update %%%%%%%%%%%%%%%%%%%%%%%%%%%
sum_y = sum_y - ym(i,:).*sinm(i,:);% remove the relevant component from the sum
ym(i,:) = (2/alpha*opedoub + Bdoubm)\(Bm'* (s - sum_x - sum_y - u - lamuda/alpha)');
%%%%%%%%%%%%% update the IFs %%%%%%%%%%%%%%%%%%%%%%%%
ybar = Differ(ym(i,:),1/fs); xbar = Differ(xm(i,:),1/fs);%compute the derivative of the functions
deltaIF = (xm(i,:).*ybar - ym(i,:).*xbar)./(xm(i,:).^2 + ym(i,:).^2)/2/pi;% obtain the frequency increment by arctangent demodulation
deltaIF = (2/betathr*opedoub + speye(N))\deltaIF';% smooth the frequency increment by low pass filtering
eIF(i,:) = eIF(i,:) - 0.5*deltaIF';% update the IF
%%%%%%%%%%%%% update cos and sin functions %%%%%%%%%%%%%%%%%%%%%%%%
sinm(i,:) = sin(2*pi*(cumtrapz(t,eIF(i,:))));
cosm(i,:) = cos(2*pi*(cumtrapz(t,eIF(i,:))));
%%%%%%%%%%%%% update sums %%%%%%%%%%%%%%%%%
sum_x = sum_x - interx + xm(i,:).*cosm(i,:); %
sum_y = sum_y + ym(i,:).*sinm(i,:);%
ssetiter(i,:,iter+1) = xm(i,:).*cosm(i,:) + ym(i,:).*sinm(i,:);%
end
IFsetiter(:,:,iter+1) = eIF;
%%%%%%%%%%%%% update Lagrangian multiplier %%%%%%%%%%%%%%%%%
lamuda = lamuda + alpha*(u + sum_x + sum_y -s);
%%%%%%%%%%%%%%%%%%%%%%%%%%% restart scheme %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
if norm(u + sum_x + sum_y -s)>norm(s) %
lamuda = zeros(1,length(t));
for i = 1:K
Bm = spdiags(sinm(i,:)', 0, N, N);Bdoubm = spdiags((sinm(i,:).^2)', 0, N, N);%
Am = spdiags(cosm(i,:)', 0, N, N);Adoubm = spdiags((cosm(i,:).^2)', 0, N, N);%
xm(i,:) = (2/alpha*opedoub + Adoubm)\(Am'*s(:));
ym(i,:) = (2/alpha*opedoub + Bdoubm)\(Bm'*s(:));
ssetiter(i,:,iter+1) = xm(i,:).*cosm(i,:) + ym(i,:).*sinm(i,:);
end
sum_x = sum(xm.*cosm,1);%
sum_y = sum(ym.*sinm,1);%
end
%%%%%%%%%%%%% compute the convergence index %%%%%%%%%%%%%%%%%%
sDif = 0;
for i = 1:K
sDif = sDif + (norm(ssetiter(i,:,iter+1) - ssetiter(i,:,iter))/norm(ssetiter(i,:,iter))).^2;
end
iter = iter + 1;
end
IFmset = IFsetiter(:,:,1:iter);
smset = ssetiter(:,:,1:iter);
IA = sqrt(xm.^2 + ym.^2);
end
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
[1]Chen S, Dong X, Peng Z, et al, Nonlinear Chirp Mode Decomposition: A Variational Method, IEEE Transactions on Signal Processing, 2017.
[2]Chen S, Dong X, Xing G, et al, Separation of Overlapped Non-Stationary Signals by Ridge Path Regrouping and Intrinsic Chirp Component Decomposition, IEEE Sensors Journal, 2017.
[3]S. Chen, Z. Peng, Y. Yang, et al, Intrinsic chirp component decomposition by using Fourier Series representation, Signal Processing, 2017, 137: 319-327.