机器学习02-再识K邻近算法（自定义数据集训练及测试）

定义：

如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别，则该样本也属于这个类别。简单的说就是根据你的“邻居”来推断出你的类别。

用个成语就是物以类聚

思想：

如果一个样本在特征空间中的K个最相邻的样本中的大多数属于某一个类别，则该样本也属于这个类别，并具有这个类别上样本的特性。该方法在确定分类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。KNN方法在类别决策时，只与极少量的相邻样本有关。由于KNN方法主要靠周围有限的邻近的样本，而不是靠判别类域的方法来确定所属类别的，因此对于类域的交叉或重叠较多的待分样本集来说，KNN方法较其他方法更为适合。

流程：

KNN算法的详细步骤如下：

数据准备：

收集训练数据集：包含已知类别（或目标值）的样本及其对应的特征。这些样本将用于训练模型。
收集测试数据集：包含待预测的新样本，同样也有相应的特征，但没有类别（或目标值）信息。这些样本将用于测试模型的性能。

距离度量：

选择一个适当的距离度量方法，例如欧氏距离、曼哈顿距离、余弦距离等。欧氏距离是最常用的度量方法。

选择K值：

选择一个合适的K值，它决定了在预测时要考虑多少个最近邻。K值的选择对算法的性能至关重要。

预测过程：

对于每个测试样本，在训练集中计算其与所有训练样本的距离。
选择与测试样本距离最近的K个训练样本。
对于分类任务，通过投票机制（majority voting）确定测试样本的类别：将K个最近邻的类别进行统计，选择出现次数最多的类别作为测试样本的预测类别。
对于回归任务，对K个最近邻的目标值进行平均，得到测试样本的预测值。

KNN 算法简单使用

from sklearn.neighbors import KNeighborsClassifier

'''
1.获取数据集
2.数据基本处理（该案例中省略）
3.特征工程（该案例中省略）
4.机器学习
5.模型评估（该案例中省略）
'''

# 构造数据集
x = [[0], [1], [2], [3]]
y = [0, 0, 1, 1]

# 机器学习 -- 模型训练
# 实例化API
estimator = KNeighborsClassifier(n_neighbors=2)
# 使用fit方法进行训练
estimator.fit(x, y)
# predict 方法进行预测
print(estimator.predict([[6]]))

结果：

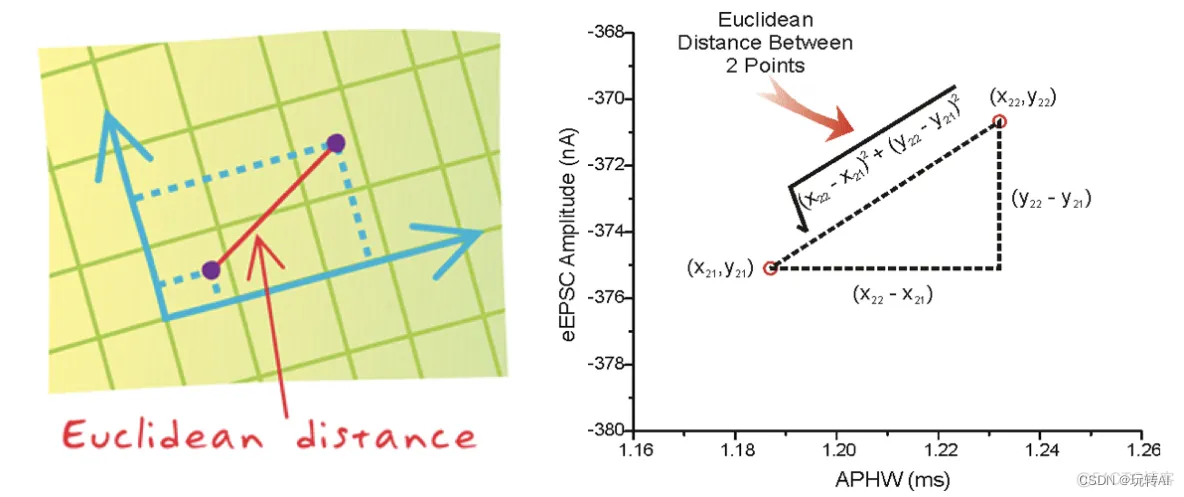
距离度量：

两个样本之间的距离可以公式计算，又叫欧式距离。
在这里插入图片描述

举例:电影类型预测

假设我们有几步电影，类别如下：

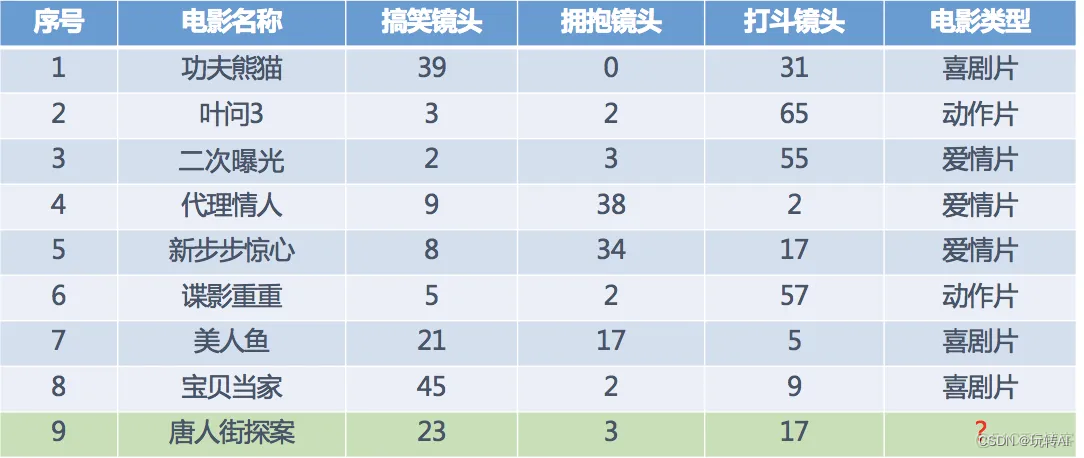
在这里插入图片描述
其中？号电影不知道类别，如何去预测？

我们可以利用K近邻算法的思想:

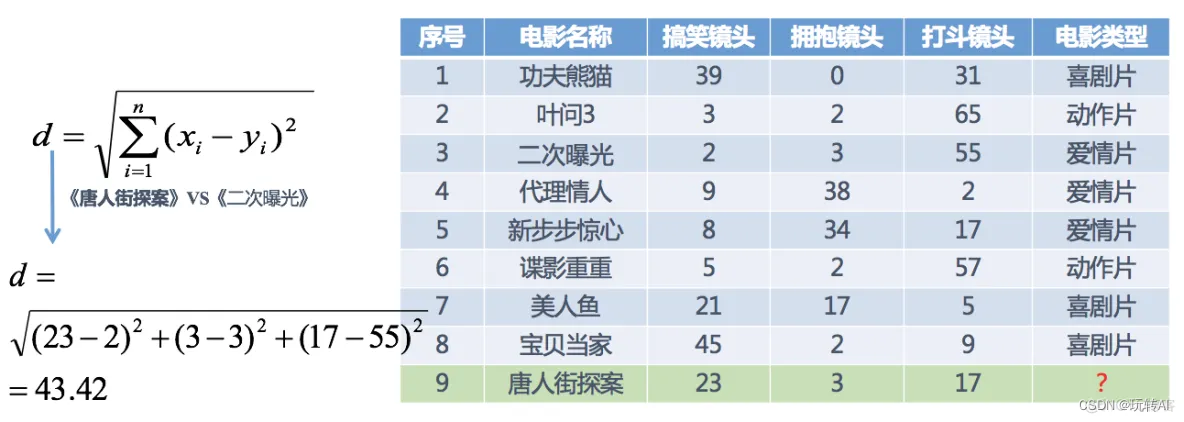
在这里插入图片描述
分别计算每个电影和被预测电影的距离，然后求解:

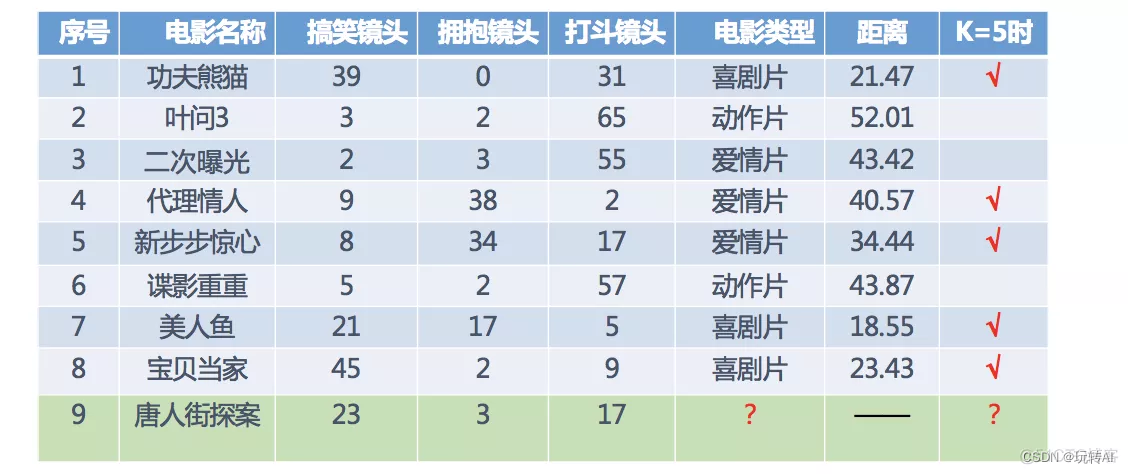
k一般选择奇数，避免出现偶数结果均分的情况。k=5，选择距离最小的五个，然后看电影类型是三个喜剧、2个爱情片，因此我们猜测唐人街探案是喜剧片。

总结流程：

1）计算已知类别数据集中的点与当前点之间的距离

2）按距离递增次序排序

3）选取与当前点距离最小的k个点

4）统计前k个点所在的类别出现的频率

5）返回前k个点出现频率最高的类别作为当前点的预测分类

实验

基于numpy然后实现，如下：
(1). numpy 有linalg 模块用于科学计算

import numpy as np 
#模拟计算唐人街探案和工夫熊猫距离
testData=[23, 3, 17]
dist = np.linalg.norm(np.array([39, 0, 31]) - np.array(testData))
print(dist)
print(round(dist, 2))

运行结果

21.470910553583888
21.47

实验2 将上面电影数据集改成代码验证

import numpy as np


def createDataset():
    '''
    创建训练集,特征值分别为搞笑镜头、拥抱镜头、打斗镜头的数量
    '''
    learning_dataset = {"功夫熊猫": [39, 0, 31, "喜剧片"],
                        "叶问3": [3, 2, 65, "动作片"],
                        "二次曝光": [2, 3, 55, "爱情片"],
                        "代理情人": [9, 38, 2, "爱情片"],
                        "新步步惊心": [8, 34, 17, "爱情片"],
                        "谍影重重": [5, 2, 57, "动作片"],
                        "美人鱼": [21, 17, 5, "喜剧片"],
                        "当家报备": [45, 2, 9, "喜剧片"]}
    return learning_dataset


def kNN(learning_dataset, dataPoint, k):
    '''
    kNN算法,返回k个邻居的类别和得到的测试数据的类别
    '''
    # s1:计算一个新样本与数据集中所有数据的距离
    disList = []
    for key, v in learning_dataset.items():
        # 对距离进行平方和开根号
        d = np.linalg.norm(np.array(v[:3]) - np.array(dataPoint))
        # round四舍五入保留两位小数，并添加到集合中
        disList.append([key, round(d, 2)])

    # s2:按照距离大小进行递增排序
    disList.sort(key=lambda dis: dis[1])  # 常规排序方法，熟悉key的作用
    print(disList)
    # s3:选取距离最小的k个样本
    disList = disList[:k]
    # s4:确定前k个样本所在类别出现的频率，并输出出现频率最高的类别
    labels = {"喜剧片": 0, "动作片": 0, "爱情片": 0}
    # 从k个中进行统计哪个类别标签最多
    for s in disList:
        # 取出对应标签
        label = learning_dataset[s[0]]
        labels[label[len(label) - 1]] += 1
    labels = sorted(labels.items(), key=lambda asd: asd[1], reverse=True)

    return labels, labels[0][0]


if __name__ == '__main__':
    learning_dataset = createDataset()
    testData = {"唐人街探案": [23, 3, 17, "？片"]}
    dataPoint = list(testData.values())[0][0:3]

    k = 5
    labels, result = kNN(learning_dataset, dataPoint, k)
    print(labels, result, sep='\n')

运行结果：

[['美人鱼', 18.55], ['功夫熊猫', 21.47], ['当家报备', 23.43], ['新步步惊心', 34.44], ['代理情人', 40.57], ['二次曝光', 43.42], ['谍影重重', 43.87], ['叶问3', 52.01]]
[('喜剧片', 3), ('爱情片', 2), ('动作片', 0)]
喜剧片

KD 树 (选择K值)

上面K最近邻算法存在一个问题就是，如果要预测一个值，需要计算该值与每一个训练集的距离，计算并存储好以后，再查看K近邻。当训练集很大时，计算非常耗时。为了提高KNN搜索的效率，考虑用特殊的数据结构存储训练数据，以减小计算距离的次数，因此引入了kd树

1. 什么是kd树

为了避免每次都重新计算一遍距离，算法会把距离信息保存在一颗树里，在计算之前从树里查询距离信息，这样避免重新计算。其基本原理是

如果A和B距离都很远，B和C距离很近，那么A和C的距离也很远。

类比“二分查找”：给出一组数据：[9 1 4 7 2 5 0 3 8]，要查找8。如果挨个查找（线性扫描），那么将会把数据集都遍历一遍。而如果排一下序那数据集就变成了：[0 1 2 3 4 5 6 7 8 9]，按前一种方式我们进行了很多没有必要的查找，现在如果我们以5为分界点，那么数据集就被划分为了左右两个“簇” [0 1 2 3 4]和[6 7 8 9]。因此，根本就没有必要进入第一个簇，可以直接进入第二个簇进行查找。把二分查找中的数据点换成k维数据点，这样的划分就变成了用超平面对k维空间的划分。空间划分就是对数据点进行分类，“挨得近”的数据点就在一个空间里面。

还有另一种变种是Ball Tree，在kd树上进行了进一步的优化。

构造kd树时需要解决2个问题：

选择向量的哪一维度进行划分？
可以选择随机或者顺序按维度选择，更好的办法应该是在数据比较分散的维度进行划分(根据方差衡量)

如何划分数据？
可以每次选择中位数来进行划分。

简单的例子

树的建立

给定一个二维空间数据集：T={(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)}，构造一个平衡kd树。

在这里插入图片描述
(1)确定先划分的维度：

import numpy as np

x = np.array([(2, 3), (5, 4), (9, 6), (4, 7), (8, 1), (7, 2)])
print(np.var(x, axis=0))

运行结果：

[5.80555556 4.47222222]

可以看到x轴的方差较大，数据分散，因此选择x轴先划分；

(2)确定根节点：

import numpy as np

x = np.array([(2, 3), (5, 4), (9, 6), (4, 7), (8, 1), (7, 2)])
print(np.median(x, axis=0))

运行结果

[6.  3.5]

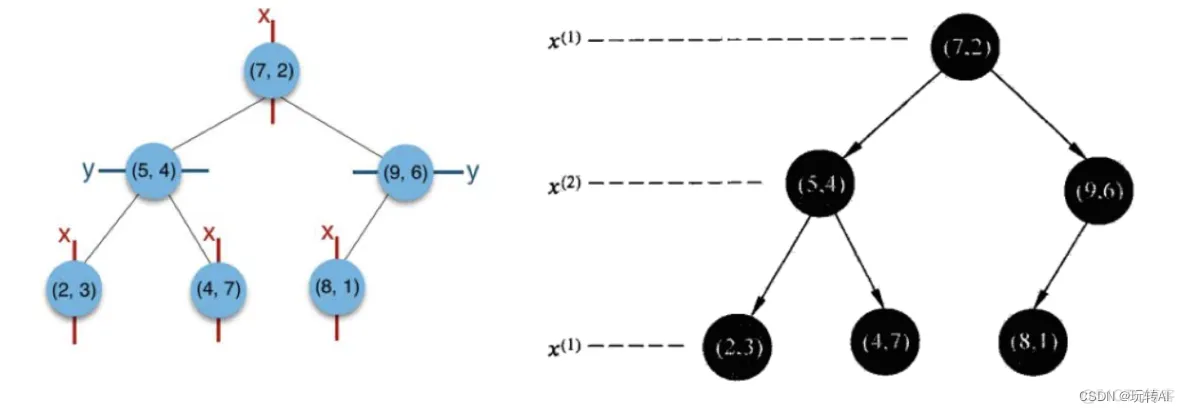
可以看到x轴的中位数是6，我们选择7 作为根节点。通过（7,2）并垂直于x轴的直线x = 7 将空间分为左右两个子矩形。

x<=7为左子空间，包含三个点[(5, 4), (2, 3), (4, 7)]

x>7包含两个节点，[(9, 6), (8, 1)]

(3)接着对左子空间和右子空间进行递归划分，直到子空间剩余一个点。

左子空间和右子空间选择中位数，然后垂直于y轴进行划分

1》左子空间选择y轴中位数4对应的点(5, 4)，垂直y轴进行划分，分为上下两个区域，每个包含一个点

2》右子空间选择y轴为9的(9, 6) 点垂直y轴划分，分为上下两个区域(因为右边就两个点，中位数为8.5, 我们选择9)

(4)接下来继续对(3)划分后的区域进行划分，垂直x轴进行划分。

经过这次划分后，区域就被完全的划分开。

最终生成的结果如下：

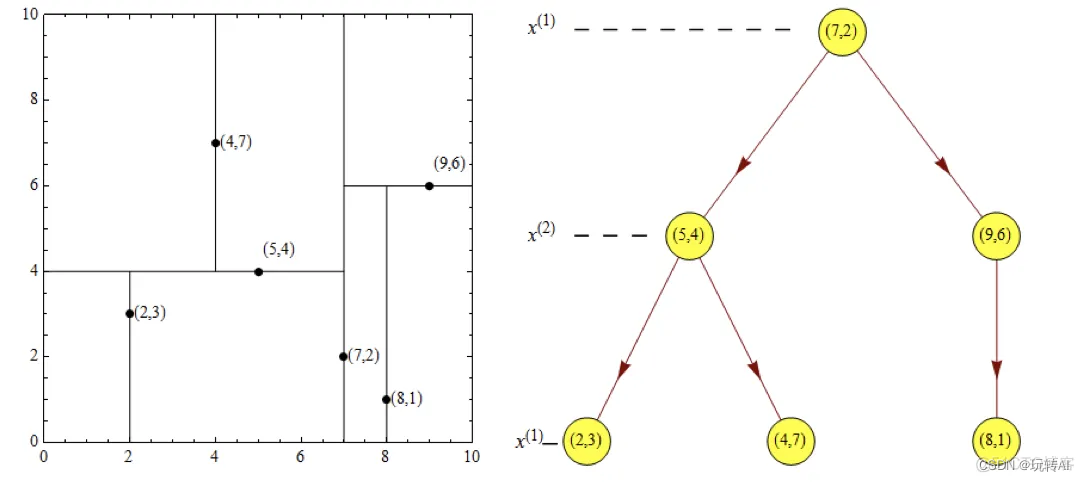
在这里插入图片描述
2. 树搜索

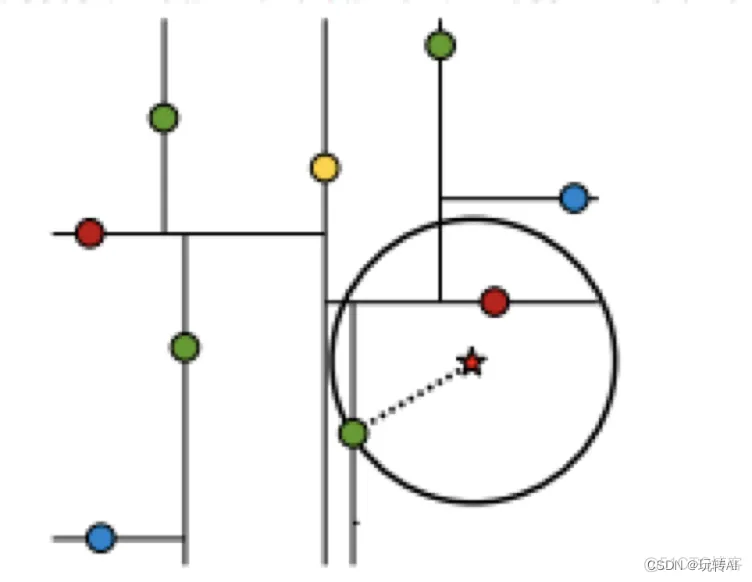
最近领域搜索

假设标记位（7,2 ）星星的点是 test point，绿色的点是找到的近似点。

在回溯过程中，需要用到一个队列，存储需要回溯的点，在判断其他子节点空间中是否有可能有距离查询点更近的数据点时，做法是以查询点为圆心，以当前的最近距离为半径画圆，这个圆称为候选超球，如果圆与回溯点的轴相交，则需要将轴另一边的节点都放到回溯队列里面来。

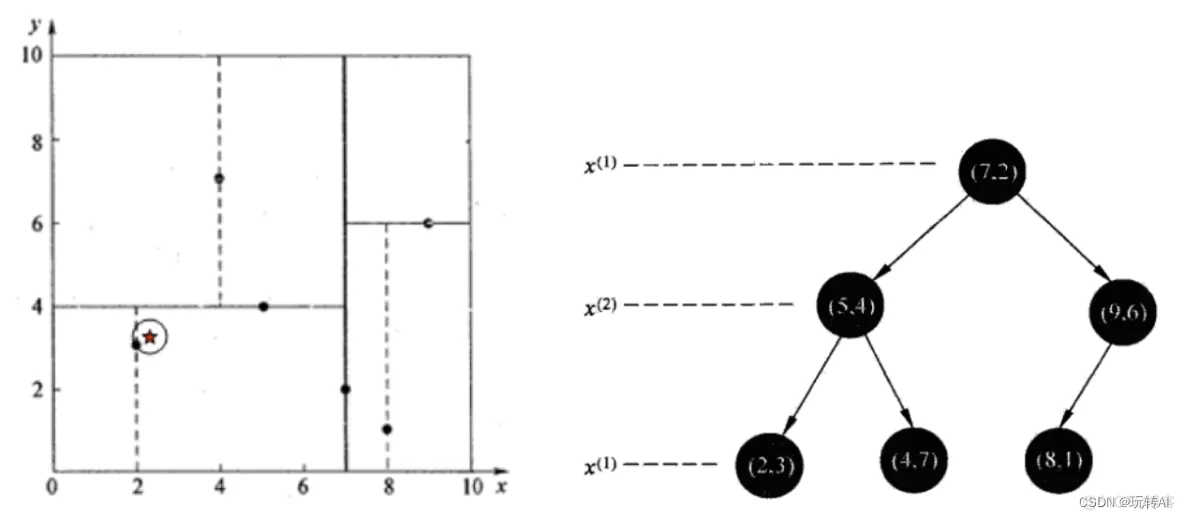
在这里插入图片描述

查找点 (2.1, 3.1)

在这里插入图片描述

通过二叉搜索，顺着搜索路径很快就能找到最邻近的叶子节点(2, 3)。而叶子节点并不一定就是最邻近的。为了找到真正的最近，还需要进行回溯操作：沿着搜索路径泛型查找是否有距离更近的点。

上面搜索路径为[(7, 2), (5, 4), (2, 3)]。搜索过程如下：

以(2,3)作为最邻近点，计算(2.1, 3.1) 到(2, 3) 的距离为：

import numpy as np

x = np.array([(2, 3)])
x1 = np.array([(2.1, 3.1)])
print(np.linalg.norm(x1 - x))

0.14142135623730964

回溯到父节点(5, 4)，判断在该区域是否有距离更近的点

以(2.1, 3.1)为圆心，0.1414 为半径画圆，发现圆并不和超平面y=4 相交，因此不用进入(5, 4) 节点的右子空间搜索

回溯到父节点(7, 2)
同样以0.1414 为半径画圆，发现不会与x=7的超平面相交，因此不用进入(7, 2)右子空间查找。

至此确定了最近的距离是(2, 3)，距离为0.1414

查找点(2, 4.5)

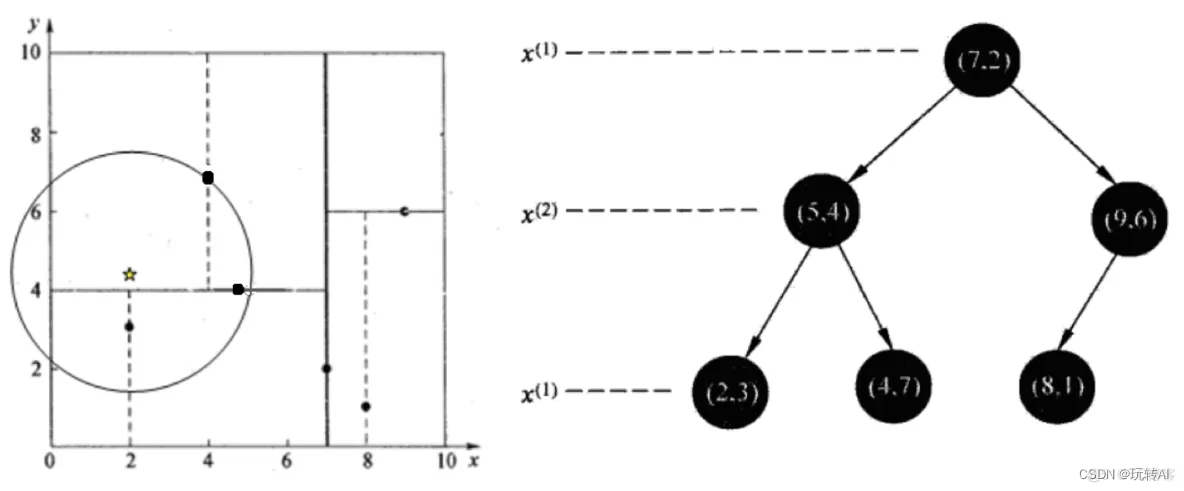
在这里插入图片描述
在(7,2)处测试到达(5,4)，在(5,4)处测试到达(4,7)，然后search_path中的结点为[(7,2),(5,4), (4,7)]，从search_path中取出(4,7)作为当前最佳结点nearest, dist为3.202。

回溯到5, 4, 以半径3.2 画圆，发现与超平面7=4 相交，所以需要跳到(5, 4)的左子空间搜索，所以将(2, 3) 加入search_path, search_path 为 [(7, 2), (2, 3)];
(5, 4) 到(2, 4.5)的距离为3.202, 因此将(5,4)赋给nearest，并且dist=3.04

回溯至(2, 3) 节点。 (2, 3) 是叶子节点，直接判断(2, 3)是否离(2, 4.5)更近，计算得到距离为1.5。所以nearest更新为(2,3)，dist更新为1.5
回溯至(7, 2)，以(2,4.5)为圆心、1.5 为半径画圆，发现与x=7的超平面没有相交，因此不用到右子空间去查找。
至此找到nearest(2,3)作为(2,4.5)的最近邻点，最近距离为1.5

预测过程

交叉验证
交叉验证：将拿到的训练数据，分为训练和验证集。以下图为例：将数据分成4份，其中一份作为验证集。然后经过4次(组)的测试，每次都更换不同的验证集。即得到4组模型的结果，取平均值作为最终结果。又称4折交叉验证。

数据分为训练集和测试集，但是为了让从训练得到模型结果更加准确。做以下处理

训练集：训练集+验证集
测试集：测试集

在这里插入图片描述
2. 网格搜索
通常情况下，有很多参数是需要手动指定的（如k-近邻算法中的K值），这种叫超参数。但是手动过程繁杂，所以需要对模型预设几种超参数组合。每组超参数都采用交叉验证来进行评估。最后选出最优参数组合建立模型。

在这里插入图片描述
3. api
sklearn.model_selection.GridSearchCV(estimator, param_grid=None,cv=None)
对估计器的指定参数值进行详尽搜索
estimator：估计器对象
param_grid：估计器参数(dict){“n_neighbors”:[1,3,5]}
cv：指定几折交叉验证

fit：输入训练数据
score：准确率
结果分析：
bestscore__:在交叉验证中验证的最好结果
bestestimator：最好的参数模型
cvresults:每次交叉验证后的验证集准确率结果和训练集准确率结果

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier

# 1、获取数据集
iris = load_iris()

# 2、数据基本处理 -- 划分数据集
x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, random_state=22)

# 3、特征工程：标准化
# 实例化一个转换器类
transfer = StandardScaler()
# 调用fit_transform
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)

# 4、KNN预估器流程
#  4.1 实例化预估器类
estimator = KNeighborsClassifier()
# 4.2 模型选择与调优——网格搜索和交叉验证
# 准备要调的超参数
param_dict = {"n_neighbors": [1, 3, 5]}
estimator = GridSearchCV(estimator, param_grid=param_dict, cv=3)
# 4.3 fit数据进行训练
estimator.fit(x_train, y_train)

# 5、评估模型效果
# 方法a：比对预测结果和真实值
y_predict = estimator.predict(x_test)
print("比对预测结果和真实值：\n", y_predict == y_test)
# 方法b：直接计算准确率
score = estimator.score(x_test, y_test)
print("直接计算准确率：\n", score)

# 评估查看最终选择的结果和交叉验证的结果
print("在交叉验证中验证的最好结果：\n", estimator.best_score_)
print("最好的参数模型：\n", estimator.best_params_)
print("每次交叉验证后的准确率结果：\n", estimator.cv_results_)

运行结果:

比对预测结果和真实值：
 [ True  True  True  True  True  True  True False  True  True  True  True
  True  True  True  True  True  True False  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True]
直接计算准确率：
 0.9473684210526315
在交叉验证中验证的最好结果：
 0.9732100521574205
最好的参数模型：
 {'n_neighbors': 5}
每次交叉验证后的准确率结果：
 {'mean_fit_time': array([0.0003287 , 0.00033251, 0.00033236]), 'std_fit_time': array([0.00046485, 0.00047025, 0.00047002]), 'mean_score_time': array([0.00198126, 0.00167513, 0.00099699]), 'std_score_time': array([3.81012484e-05, 4.79384769e-04, 2.24783192e-07]), 'param_n_neighbors': masked_array(data=[1, 3, 5],
             mask=[False, False, False],
       fill_value='?',
            dtype=object), 'params': [{'n_neighbors': 1}, {'n_neighbors': 3}, {'n_neighbors': 5}], 'split0_test_score': array([0.97368421, 0.97368421, 0.97368421]), 'split1_test_score': array([0.97297297, 0.97297297, 0.97297297]), 'split2_test_score': array([0.94594595, 0.89189189, 0.97297297]), 'mean_test_score': array([0.96420104, 0.94618303, 0.97321005]), 'std_test_score': array([0.01291157, 0.03839073, 0.00033528]), 'rank_test_score': array([2, 3, 1])}