这里先贴题目：

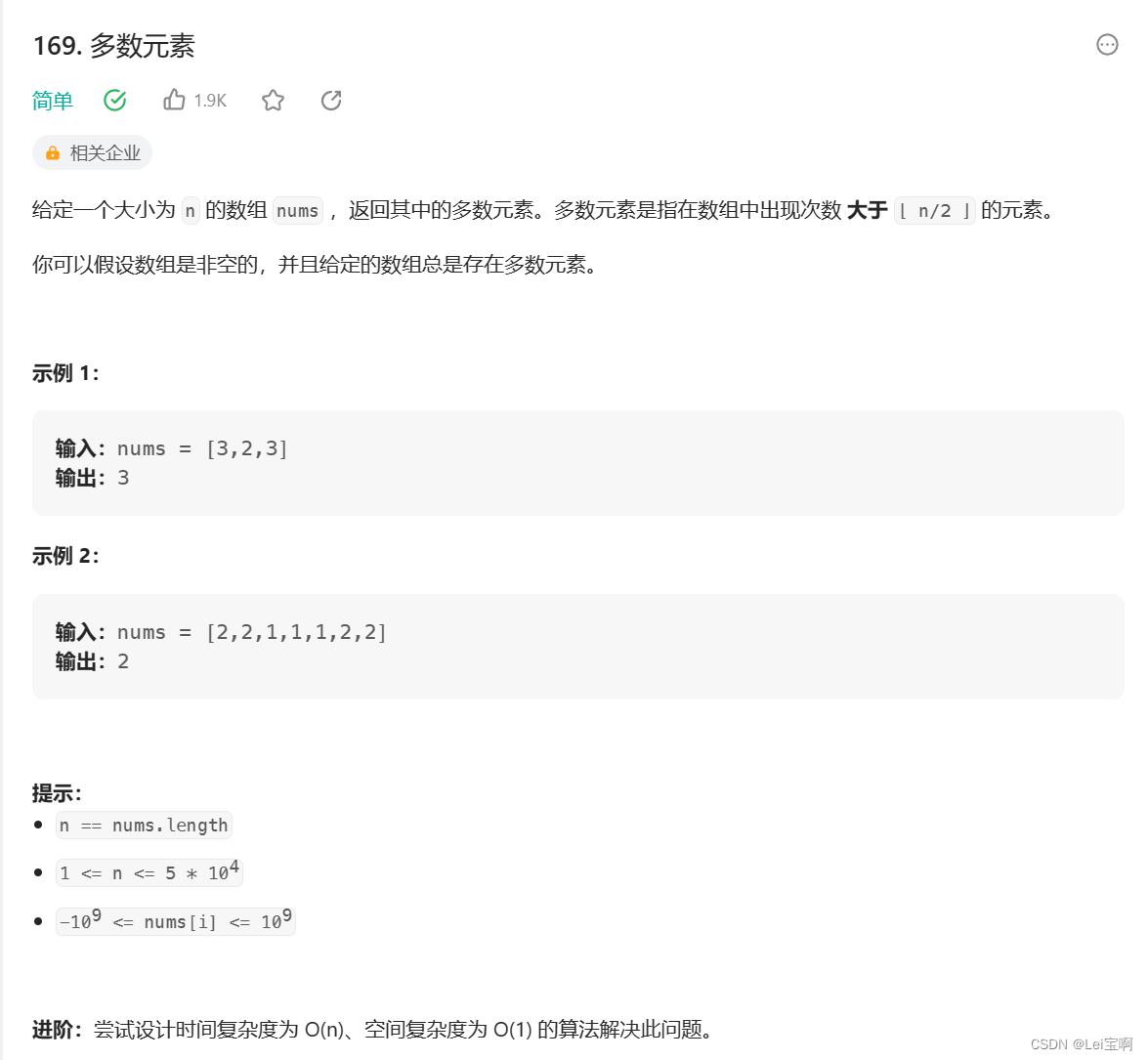
Boyer-Moore 投票算法：

通俗点来讲，就是占领据点，像攻城那样，对消。

当你的据点有人时对消，无人时就占领。

 这道题使用该算法可实现时间复杂度为O(n),空间复杂度为O(1)，接下来看代码：

int majorityElement(int* nums, int numsSize) {

    int amzing = nums[0];

    int count = 0;
    for (int i = 0; i < numsSize; i++)
    {
        if (amzing == nums[i])
            count++;
        else if (count == 0)
        {
            amzing = nums[i];
            count++;
        }
        else
            count--;
    }
    return amzing;
}

 我们定义一个amzing先记录数组第一个数字，并且数量为0，然后遍历整个数组，当count不为0时，数字不同时相消，数字相同时增加，当count为0时，amzing换其他数字，再增加数量。

通俗点讲：定义一个士兵，数量为0，遍历所有人，当count不为0，如果数字不同，就是遇到敌人，同归于尽，数字相同，遇到友军就加入。当count等于0，据点无人，哪个数字也可以占领。但是有一个阵营的人数占了大半，无论怎么对拼相消，剩下的一定是那个阵营的，也就是那个大半的数字。 

排序：

int cmp(void* p1,void* p2)
{
    return *(int*)p1 - *(int*)p2;
}

int majorityElement(int* nums, int numsSize){

    qsort(nums,numsSize,4,cmp);
    return nums[numsSize/2];
}