题目

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

• 节点的左子树只包含 小于 当前节点的数。
• 节点的右子树只包含 大于 当前节点的数。
• 所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

输入：root = [2,1,3]
输出：true

示例 2：

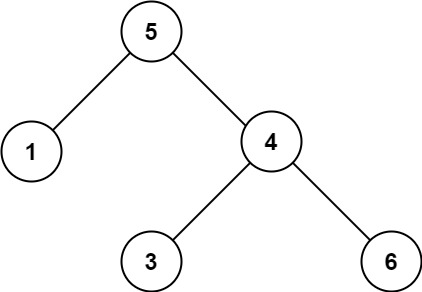
输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

提示：

• 树中节点数目范围在[1, 104] 内
• -231 <= Node.val <= 231 - 1

解答

源代码

class Solution {
    public boolean isValidBST(TreeNode root) {
        return isValidBST(root, Long.MIN_VALUE, Long.MAX_VALUE);
    }

    public boolean isValidBST(TreeNode node, long low, long high) {
        if (node == null) {
            return true;
        }

        if (node.val <= low || node.val >= high) {
            return false;
        }

        return isValidBST(node.left, low, node.val) && isValidBST(node.right, node.val, high);
    }
}

总结

我一开始的想法是遍历过程中比较左右子节点的值和当前节点的值，如果有问题就返回false，全部遍历完之后没问题就返回true，但是我没有注意到是需要左子树的所有节点都小于当前节点，右子树所有节点大于当前节点，所以学习了题解的思路，在每次遍历时，记录上当前节点的合法范围。

当递归进入当前节点的左子节点时，因为左子树的节点都小于当前节点，所以节点合法范围的最大值应设为当前节点，右子节点同理。