数据结构笔记

1.  绪论

随着计算机深入到各个领域，它的作用已不再局限于科学计算，而更多的用于控制，管理及数据处理等非数值计算的处理工作。而它加工出理的对象也由纯粹的数值发展到字符，表格和图像等各种具有一定结构的数据。一个“好”的程序，必须分析待处理的对象的特性以及各处理对象之间存在的关系。这就是数据结构这门学科产生的背景。

1.1  什么是数据结构？

数据结构是一门研究非数值计算的程序设计问题中计算机的操作对象以及它们之间的关系和操作等等的学科。

数据结构是计算机存储、组织数据的方式，是数据之间表现关系和处理关系的一种形式

作用（好处）：可以带来更高的运行效率或者存储效率

1.2  数据结构的划分

1、线性结构：在数据元素的非空有限集合中，存在唯一一个被称做“第一个”的元素，存在唯一一个被称做“最后一个”的元素，除        第一个之外，集合中的每个数据元素均只有一个前驱，除最后一个以外，每一个元素都只有一个直接后继。

2、非线性结构：一个数据元素可能有多个直接前趋和多个直接后继

1.3  数据结构的术语

逻辑（数据）结构：数据元素之间的逻辑关系

存储（物理）结构：数据结构在计算机中的表示

算法的设计取决于逻辑结构而算法的实现依赖于采用的存储结构

时间复杂度：定量描述了该算法的运行时间        n：元素的个数

时间复杂度的大小排序： O(1) 、O(log n)、O(n)、O(nlog n) 、O(n^2) 、O(n^3)、 O(2^n)

                                       O(1)：字典取值 、list.pop()

                                       O(log n)：二分查找

                                       O(n)：遍历、list.get（index）

                                       O(nlog n)：快速排序、归并排序

                                       O(n^2)：冒泡、选择排序                             

空间复杂度：空间复杂度是指执行这个算法所需要的内存空间

2、线性表

2.1  线性表的逻辑结构

n个数据元素的有限序列  最常用  最简单

2.2  线性表的顺序存储

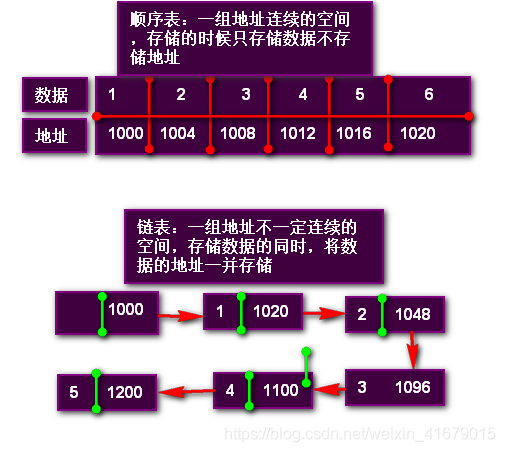
顺序表：一组地址连续的存储单元依次存储线性表的数据元素，即逻辑相邻的元素，物理位置上也必须相邻。只有数据域（储存数据元素信息的域）

用途：（1）需要根据序号进行随机查找的数据

            （2）数据定长的且所需内存不太大的数据

特点：地址连续，确定了起始位置，可以进行随机存取。增删慢，查找快

缺点：对于长度变化比较大的顺序表，起始预留空间必须按照最大空间分配，不能充分利用存储空间，扩容难

2.3  线性表的链式存储

链表：一组任意的存储单元存储线性表的数据元素，即逻辑相邻的元素，物理位置上可以相邻，也可以不相邻。由数据域和指针域（存储直接后继存储位置的域）组成

        用途：（1）不需要根据序号进行随机查找的数据

                    （2）数据是逐渐增加的或者不定长的

                    （3）希望每次添加数据、删除数据的动作的时间复杂度都是O（1）的

                （常量时间），即需要大量增删的数据

        特点：地址不连续，无法随机存取。增删快，查找慢

3.  栈和队列

3.1  栈

3.1.1  栈的特点

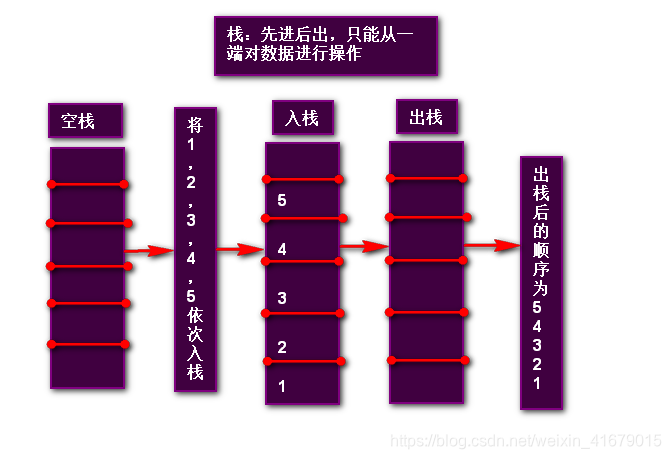
限定仅在表尾进行插入和删除操作的线性表，表尾称为栈顶，表头称为栈底，    不含元素的栈称为空栈,数据元素先进后,英文缩写FILO

3.1.2  栈的用途

用途：（1）JVM中用栈存储基本数据类型，指令代码,常量,和JVM堆中对象的引用         地址。     

      （2）动态地存储函数之间的关系，以保证被调用函数在返回                         时恢复到母函数中继续执行。

      （3）表达式求值和进制转换，主要使用在计算器上。

3.2  队列

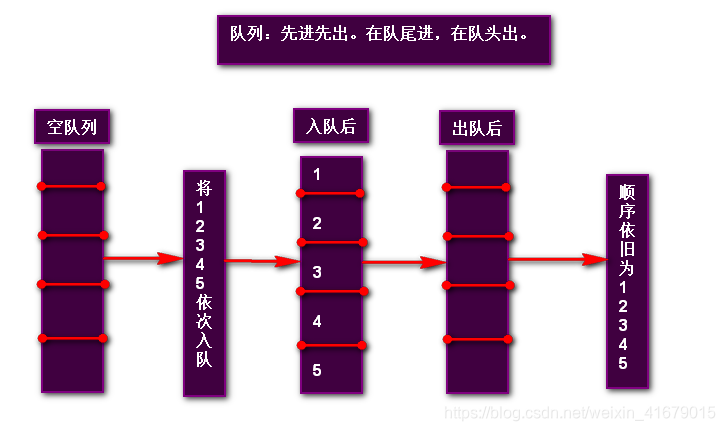
3.2.1  队列的特点

限定仅在表尾进行插入和在表头进行删除操作的线性表，表尾称为队尾，表头称为队头，数据元素先进先出，英文缩写FIFO

3.2.2  队列的应用

异步处理：使用队列的一个主要原因是进行异步处理，比如用户注册成功后需要发送注册成功邮件/新用户积分/优惠券等等、缓存过期时先返回老的数据，然后异步更新缓存、异步写日志等；通过异步处理，可以提升主流程响应速度，而非主流程/非重要业务可以异步集中处理，这样还可以将任务聚合然后批量处理；因此可以使用消息队列/任务队列来进行异步处理。

系统解耦：比如用户成功支付完成订单后，需要通知生产配货系统、发票系统、库存系统、推荐系统、搜索系统、风控系统等进行业务处理；而未来需要添加/支持哪些业务是不清楚的，而且这些业务处理不需要实时处理、不需要强一致，只需要最终一致性即可，因此可以通过消息队列/任务队列进行系统解耦。

数据同步：比如想把MySQL变更的数据同步到Redis、或者将Mysql数据同步到MongoDB、或者机房间数据同步、或者主从数据同步等，此时可以考虑使用如databus、canal、otter。使用数据总线队列进行数据同步的好处是可以保证数据修改的有序性。

流量削峰：系统瓶颈一般在数据库上，比如扣减库存、下单等；此时可以考虑使用队列将变更请求暂时放入队列，通过缓存+队列暂存的方式将数据库流量削峰；还有如秒杀系统，下单服务会是该系统的瓶颈，此时会使用队列进行排队和限流，从而保护下单服务。通过队列暂存或者队列限流来削峰。

4.串

4.1  串的特点

串（字符串），是由零个或者多个字符组成的有限序列

4.2  串的应用

等同于python中的字符串的应用

5. 数组和广义表

5.1  数组

5.1.1  数组的特点

等同于java中的数组

5.1.2  数组的用途

（1）给定一组下标，存取相应的数据元素。

（2）给定一组下标，修改相应数据元素中的某一个或者几个数据项的值

（3）矩阵的压缩存储，节约内存空间

注：数组一般不进行插入或者删除操作，所以一般用顺序结构来存储数组

5.2  广义表

线性表的扩展，线性表只能存储原子数据，而广义表的数据元素可以是线性表。主要应用于人工智能领域的表处理语言LISP语言。由于广义表的数据元素可以具有不同的结构，所以一般使用链式存储

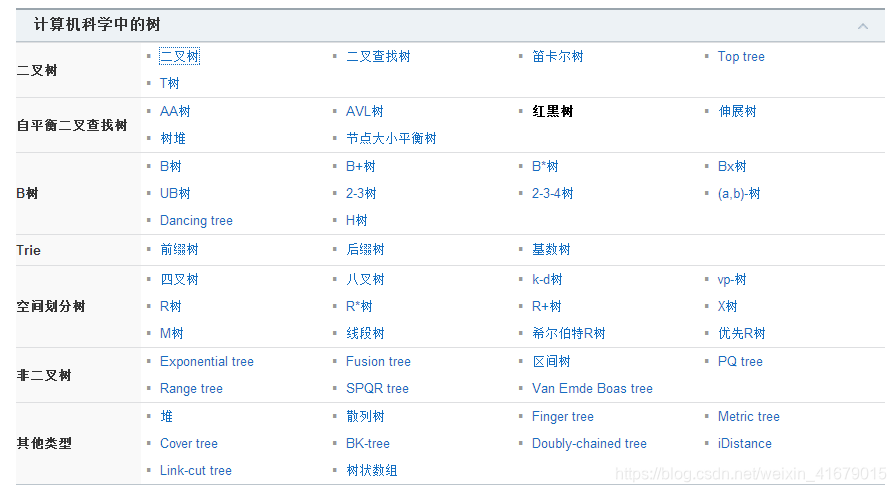
6.  树

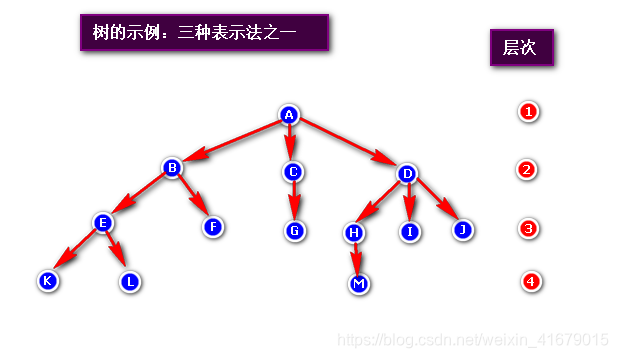
n个节点的有限集，直观的看法，树是以分支关系定义的层次结构。

    用途：（1）人类社会中的族谱和各种社会机构组织

         （2）文件目录结构

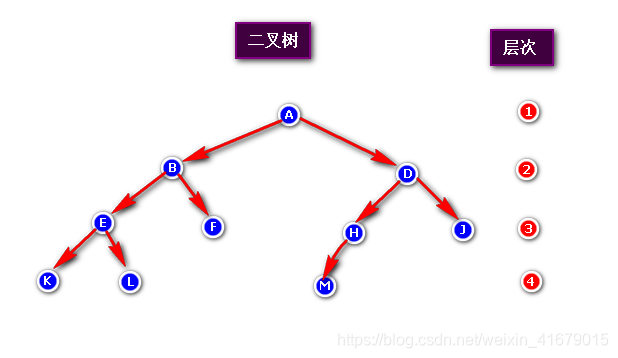
6.1  二叉树

一种树结构，每个节点至多只有两个子树，且子树有左右子树之分，其次序不能随意颠倒

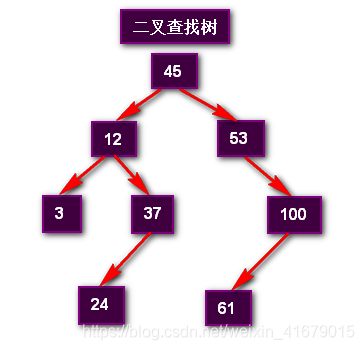
6.2  二叉查找树

又称二叉搜索树或二叉排序树或者B树，是最基本的查找树，是AVL树，红黑树等查找树的基础。

6.2.1  二叉查找树的特点

二叉查找树或者是一棵空树，或者是具有下列性质的二叉树：

(1)若左子树不空，则左子树上所有结点的值均小于或等于它的根结点的值；

(2)若右子树不空，则右子树上所有结点的值均大于或等于它的根结点的值；

(3)左、右子树也分别为二叉查找树；

6.2.2  二叉查找树的应用

基本不用最原始的二叉查找树，而使用比它性能更好的变种树等

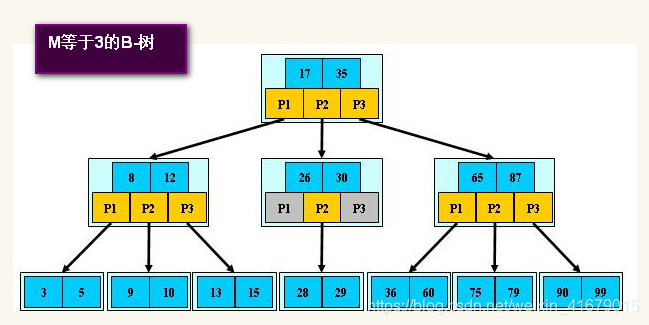
6.3  B-树

6.3.1  B-树的特点

6.3.2  B-树的应用

主要用在文件系统

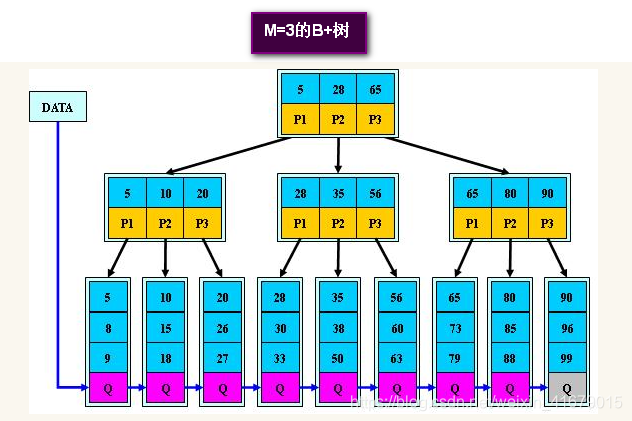
6.4  B+树

6.4.1  B+树的特点

  1.其定义基本与B-树同，除了：

       非叶子结点的子树指针与关键字个数相同；

       非叶子结点的子树指针P[i]，指向关键字值属于[K[i], K[i+1])的子树

            （B-树是开区间）；

       为所有叶子结点增加一个链指针；

       所有关键字都在叶子结点出现；

6.4.2   B+树的应用

用在文件系统，数据索引和数据库索引

6.4.3  B+树的优点

1. B+-tree的磁盘读写代价更低

内部结点并没有指向关键字具体信息的指针。因此其内部结点相对B 树更小，可以有更多非叶子节点存放在再内存中，减少大量的IO

1. B+-tree的查询效率更加稳定

由于非终结点并不是最终指向文件内容的结点，而只是叶子结点中关键字的索引。所以任何关键字的查找必须走一条从根结点到叶子结点的路。所有关键字查询的路径长度相同，导致每一个数据的查询效率相当。

1. 方便扫库

B树必须用中序遍历的方法按序扫库，而B+树直接从叶子结点挨个扫一遍就完了

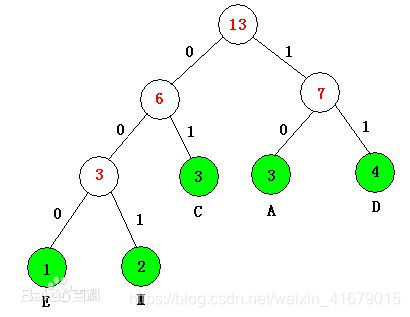
6.5  哈夫曼树

6.5.1  哈夫曼树的特点

给定n个权值作为n个叶子结点，构造一棵二叉树，若带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman Tree)

6.5.2  哈夫曼树的应用

哈夫曼编解码：用每个字母作为节点，用它们各自出现的频率作为权，构建一颗哈夫曼树，即可求得最短编码。

6.6  T树

6.6.1  T树的特点

T树是一个每个结点含有多个关键字的平衡二叉树，每个节点内的关键字有序排列，左子树都要比根节点关键字小，右子树都要比根节点关键字大。

6.6.2  T树的应用

T-tree是针对主存访问优化的索引技术，内存数据库中最主要的一种索引方式。

和B+树的区别：在无并发的情况下，T树的性能要优于B树，在有并发操作的情况下，B树的性能要好于T树

6.7  AVL树

6.7.1  AVL树的特点

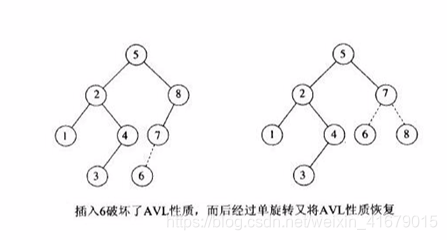
它是平衡二叉树，平衡条件非常严格（树高差只有1），只要插入或删除不满足上面的条件就要通过旋转来保持平衡

6.7.2  AVL树的应用

插入删除次数比较少，但查找多的情况，windows对进程地址空间的管理应用了AVL树

     

6.8  红黑树

6.8.1  红黑树的特点

是每个节点都带有颜色属性的二叉查找树，颜色或红色或黑色。在二叉查找树强制一般要求以外，对于任何有效的红黑树我们增加了如下的额外要求:

       1. 节点是红色或黑色。

       2. 根节点是黑色。

       3 每个叶节点（NIL节点，空节点）是黑色的。

       4 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)

       5. 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。

       特点：从根到叶子的最长的可能路径不多于最短的可能路径的两倍长，树大致平衡

6.8.2  红黑树的应用

       1、在搜索时，插入删除次数多的情况下用红黑树来取代AVL

       2、著名的linux进程调度Completely Fair Scheduler,用红黑树管理进程控                        制块

       3、epoll在内核中的实现，用红黑树管理事件块

       4、nginx中，用红黑树管理timer等

       5、Java的TreeMap实现

       6、Mysql的索引

           

1. 排序
   1. 快速排序
   2. 归并排序
   3. 插入排序
   4. 希尔排序
   5. 基数排序
   6. 堆排序
2. 图

可以转化为树，再选择一种树来解决问题。

最常见问题：最短路径