一、线性数据结构

栈、队列、双端队列和列表都是有序的数据集合，其元素的顺序取决于添加顺序或移除顺序。一旦某个元素被添加进来，它与前后元素的相对位置将保持不变。这样的数据集合经常被称为线性数据结构。

线性数据结构可以看作有两端。真正区分线性数据结构的是元素的添加方式和移除方式，尤其是添加操作和移除操作发生的位置。举例来说，某个数据结构可能只允许在一端添加新元素，有些则允许从任意一端移除元素。

二、栈

2.1 何谓栈

栈有时也被称作“下推栈 ”。它是有序集合，添加操作和移除操作总发生在同一端，即“顶端”，另一端则被称为“底端”。

栈中的元素离底端越近，代表其在栈中的时间越长，因此栈的底端具有非常重要的意义。最新添加的元素将被最先移除。这种排序原则被称作LIFO，即后进先出。它提供了一种基于在集合中的时间来排序的方式。最近添加的元素靠近顶端，旧元素靠近底端。

2.2 栈抽象数据类型

栈抽象数据类型由下面的结构和操作定义。如前所述，栈是元素的有序集合，添加操作与移除操作都发生在其顶端。栈的操作顺序是LIFO，它支持以下操作。

Stack()创建一个空栈。它不需要参数，且会返回一个空栈。
push(item)将一个元素添加到栈的顶端。它需要一个参数item，且无返回值。
pop()将栈顶端的元素移除。它不需要参数，但会返回顶端的元素，并且修改栈的内容。
peek()返回栈顶端的元素，但是并不移除该元素。它不需要参数，也不会修改栈的内容。
isEmpty()检查栈是否为空。它不需要参数，且会返回一个布尔值。
size()返回栈中元素的数目。它不需要参数，且会返回一个整数。

2.3 用Python实现栈

抽象数据类的实现被称为数据结构。

以下代码是栈的实现，它假设列表的尾部是栈的顶端。当栈增长时（即进行push操作），新的元素会被添加到列表的尾部，pop操作同样会修改这一端。

class Stack:
    def __init__(self):
        self.items=[]
        
    def isEmpty(self):
        return self.items==[]
    
    def push(self,item):
        self.items.append(item)
    
    def pop(self):
        return self.items.pop()
    
    def peek(self):
        return self.items[len(self.items)-1]
    
    def size(self):
        return len(self.items)

接下来展示上述代码中的栈操作及其返回结果。

s=Stack()
print(s.isEmpty())

s.push(4)
s.push('dog')
print(s.peek())

s.push(True)
print(s.size())

print(s.isEmpty())

s.push(8.4)
print(s.pop())

print(s.pop)

print(s.size)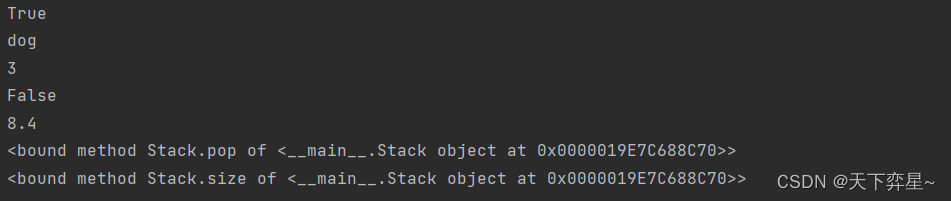

也可以选择将列表的头部作为栈的顶端。不过在这种情况下，便无法直接使用pop方法和append方法，而必须使用pop方法和insert方法显式地访问下标为0的元素，即列表中的第1个元素。代码如下：

class Stack:
    def __init__(self):
        self.items=[]

    def isEmpty(self):
        return self.items==[]

    def push(self,item):
        self.items.insert(0,item)

    def pop(self):
        return self.items.pop(0)

    def peek(self):
        return self.items[0]

    def size(self):
        return len(self.items)

尽管上述两种实现都可行，但是二者在性能方面肯定有差异。append方法和pop()方法的时间复杂度都是O(1)，这意味着不论栈中有多少个元素，第一种实现中的push操作和pop操作都会在恒定时间内完成。第二种实现的性能则受制于栈中的元素个数，这是因为insert(0)和pop(0)的时间复杂度都是O(n)，元素越多越慢。

2.4 匹配括号

由一个空栈开始，从左到右依次处理括号。如果遇到左括号，便通过push操作将其加入栈中，以此表示稍后需要有一个与之匹配的右括号。反之，如果遇到右括号，就调用pop操作。只要栈中的所有左括号都能遇到与之匹配的右括号，那么整个括号串就是匹配的；如果栈中有任何一个左括号找不到与之匹配的右括号，则括号串就是不匹配的。在处理完匹配的括号串之后，栈应该是空的。代码如下：

from pythonds.basic import Stack

def parChecker(symbolString):
    s=Stack()
    balanced=True
    index=0
    while index<len(symbolString) and balanced:
        symbol=symbolString[index]
        if symbol=="(":
            s.push(symbol)
        else:
            if s.isEmpty():
                balanced=False
            else:
                s.pop()
        index=index+1
    if balanced and s.isEmpty():
        return True
    else:
        return False

2.5 普通情况：匹配符号

from pythonds.basic import Stack

def parChecker(symbolString):
    s=Stack()
    balanced=True
    index=0
    while index<len(symbolString) and balanced:
        symbol=symbolString[index]
        if symbol in "([{":
            s.push(symbol)
        else:
            if s.isEmpty():
                balanced=False
            else:
                top=s.pop()
                if not matches(top,symbol):
                    balanced=False
        index=index+1
    if balanced and s.isEmpty():
        return True
    else:
        return False

def matches(open,close):
    opens="([{"
    closers=")]}"
    return opens.index(open)==closers.index(close)

2.6 将十进制数转换成二进制数

将十进制数转换成二进制数采用的是“除以2”算法。“除以2”算法假设待处理的整数大于0.它用一个简单的循环不停地将十进制数除以2，并且记录余数。第一次除以2的结果能够用于区分偶数和奇数。如果是偶数，则余数为0，因此个位上的数字是0；如果是奇数，则余数为1，因此个位上的数字是1.可以将要构建的二进制数看成一系列数字；计算出的第一个余数是最后一位。这体现出了反转特性，因此用栈来解决问题是合理的。

from pythonds.basic import Stack

def divideBy2(decNumber):
    remstack=Stack()
    while decNumber>0:
        rem=decNumber%2
        remstack.push(rem)
        decNumber=decNumber//2
    binString=""
    while not remstack.isEmpty():
        binString=binString+str(remstack.pop())
    return binString

将十进制数转换成任意进制数的代码如下：

from pythonds.basic import Stack

def baseConverter(decNumber,base):
    digits="0123456789ABCDEF"
    remstack=Stack()
    while decNumber>0:
        rem=decNumber%base
        remstack.push(rem)
        decNumber=decNumber//base
    newString=""
    while not remstack.isEmpty():
        newString=newString+digits[remstack.pop()]
    return newString

3.7 前序、中序和后序表达式

3.7.1 从中序到后序的通用转换法

假设中序表达式是一个以空格分隔的标记串。其中，运算符标记有*、/、+和-，括号标记有(和)，操作数标记有A、B、C等。下面的步骤会生成一个后序标记串。

（1）创建用于保存运算符的空栈opstack，以及一个用于保存结果的空列表。

（2）从左往右扫描这个标记列表。

如果标记是操作数，将其添加到结果列表的末尾。
如果标记是左括号，将其压入opstack栈中。
如果标记是右括号，反复从opstack栈中移除元素，直到移除对应的左括号。将从栈中取出的每一个运算符都添加到结果列表的末尾。
如果标记的是运算符，将其压入opstack栈中。但是，在这之前，需要先从栈中取出优先级更高或相同的运算符，并将它们添加到列表的末尾。

（3）当处理完输入表达式以后，检查opstack。将其中所有残留的运算符全部添加到结果列表的末尾。

为了在Python中实现这一算法，我们使用一个叫做prec的字典来保存运算符的优先级值。该字典把每一个运算符都映射成一个整数。通过比较对应的整数，可以确定运算符的优先级。左括号的优先级值最小。这样一来，任何与左括号比较的运算符都会被压入栈中。我们也将导入string模块，它包含一系列预定义变量。本例使用一个包含所有大写字母的字符串（string.ascii_uppercase）来代表所有可能出现的操作数。代码如下：

from pythonds.basic import Stack
import string

def infixToPostfix(infixexpr):
    prec={}
    prec['*']=3
    prec['/']=3
    prec['+']=2
    prec['-']=2
    prec['(']=1

    opStack=Stack()
    postfixList=[]

    for token in infixexpr:
        if token in string.ascii_uppercase:
            postfixList.append(token)
        elif token=='(':
            opStack.push(token)
        elif token==')':
            topToken=opStack.pop()
            while topToken != '(':
                postfixList.append(topToken)
                topToken=opStack.pop()
        else:
            while (not opStack.isEmpty()) and (prec[opStack.peek()]>=prec[token]):
                postfixList.append(opStack.pop())
            opStack.push(token)

    while not opStack.isEmpty():
        postfixList.append(opStack.pop())

    return " ".join(postfixList)

print(infixToPostfix("(A+B)*(C+D)"))

3.7.2 计算后序表达式

假设后序表达式是一个以空格分隔的标记串。其中，运算符标记有*、/、+、-，操作数标记是一位的整数值。结果是一个整数。

（1）创建空栈operandStack.

（2）使用字符串方法split将输入的后序表达式转换成一个列表。

（3）从左往右扫描这个标记列表。

如果标记是操作数，将其转换成整数并且压入operandStack栈中。

如果标记是运算符，从operandStack栈中取出两个操作数。第一次取出右操作数，第二次取出左操作数。进行相应的算数运算，然后将运算结果压入operandStack栈中。

（4）当处理完输入表达式时，栈中的值就是结果。将其从栈中返回。

from pythonds.basic import Stack
def postfixEval(postfixExpr):
    operandStack=Stack()

    tokenList=postfixExpr.split()

    for token in tokenList:
        if token in "0123456789":
            operandStack.push(int(token))
        else:
            operand2=operandStack.pop()
            operand1=operandStack.pop()
            result=doMath(token,operand1,operand2)
            operandStack.push(result)

    return operandStack.pop()

def doMath(op,op1,op2):
    if op=="*":
        return op1*op2
    elif op=="/":
        return op1/op2
    elif op=="+":
        return op1+op2
    else:
        return op1-op2