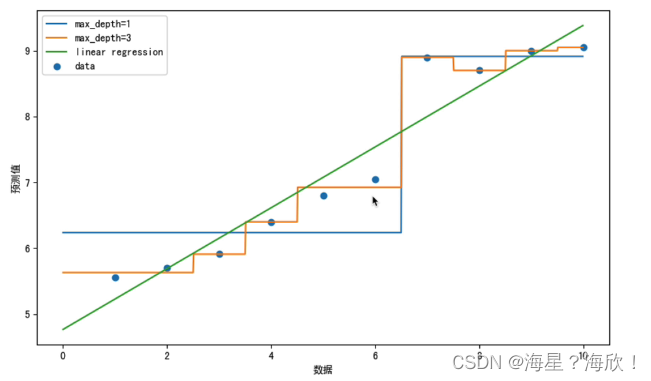
之前描述了过拟合的问题,现在介绍一些正则化模型的技术。
正则化:凡事可以减少泛化误差而不是减少训练误差的方法,都可以称作正则化方法。
我们总是可以通过去收集更多的训练数据来缓解过拟合。 但这可能成本很高,耗时颇多,或者完全超出我们的控制,因而在短期内不可能做到。
假设我们已经拥有尽可能多的高质量数据,我们便可以将重点放在正则化技术上。
在多项式回归的例子中, 我们可以通过调整拟合多项式的阶数来限制模型的容量。实际上,限制特征的数量是缓解过拟合的一种常用技术。 然而,简单地丢弃特征对这项工作来说可能过于生硬。
ps: 不断更新w和b这两个模型参数使得损失函数最小,w和b不是唯一的。也就是说,达到局部最优解可以有多组值。有可能一组w和b很大,但仍然能达到局部最优解,但是参数很大,误差和噪声也会被放大,预测会不准确。因此,可以人为地控制参数的取值范围。
权重衰退是一种最常见的处理过拟合的方法,通常也被称为L2正则化
1. 使用均方范数作为硬性条件

w权重是模型中未知数的系数,它的取值情况直接决定了模型曲线到底是什么样子的,而偏置b的取值,不会改变模型曲线的样子,只会改变模型的平移情况。L1和L2正则化,针对的是w进行,对b的处理意义不大。
使得w的每个项的平方和是小于一个特定的值,也就是说每个项的值都小于特定值的开根号。
但一般来说,我们不会直接用这个优化函数,因为相对来说麻烦一点。常用的是下面的函数。
2. 使用均方范数作为柔性限制

- 当超参数=0,就是没有起作用,等价于上一张图片中Θ等于无穷大,因为没有对模型容量进行控制。
- 当超参数趋向于无穷大时,表示惩罚项越来越大,等价于Θ趋向于0,使得最优解w* 趋向于0.
- 如果想使得模型复杂度低,可以通过增加λ满足需求
W可以选择的范围越大哦,表示模型越复杂。
较小的λ值对应较少约束的w, 而较大的λ值对w的约束更大。
3. 演示对最优解的影响
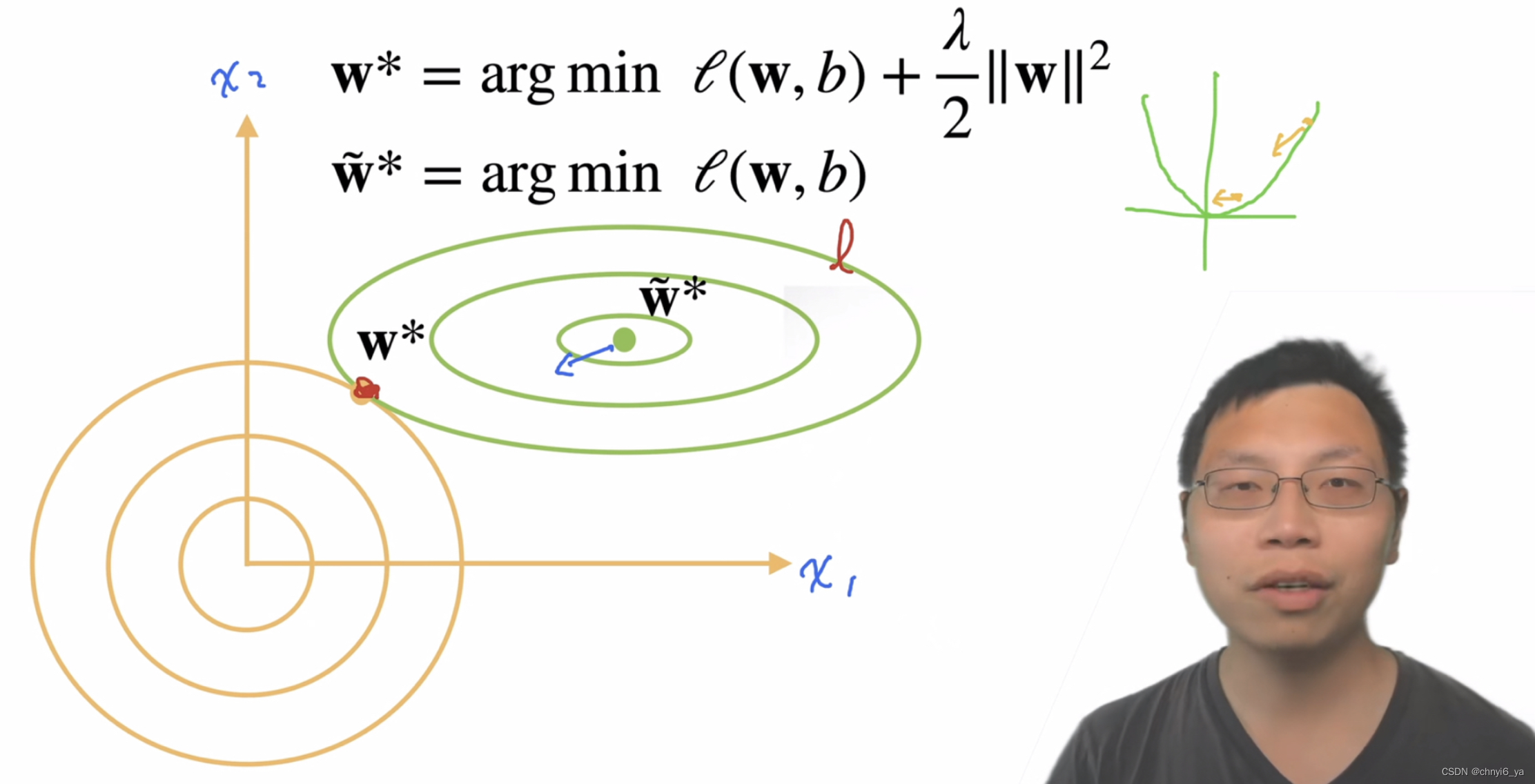
绿色曲线是损失函数的取值,黄色曲线是惩罚项的取值,两者都是圈越大取值越大。
在L2损失函数中,在优化点附近时对值的拉伸比较小,因为梯度来说相对比较小,但是离优化点比较远的时候,梯度值更大,往优化点的作用会越大。
所以,在绿色曲线的中心这一点,惩罚对这一点的拉力会大于绿色曲线loss对其的拉力,因为在最优点绿色函数梯度接近于0了,而黄色函数的梯度更大,使得参数更新时是往橙色函数方向更新,最后在两个曲线相切的地方形成平衡点。
因为目标是为了减小loss,一开始loss函数是只有一项组成,而现在加入了正则化项,在取同样的loss值时,只能通过更小的w来实现了。因此,这样就控制了w的取值范围,从而控制了模型容量。
所以,在加入了惩罚项后,也就是在橙色曲线的限制下,使得最优解往左下偏移了。这个最优解是目标函数(损失函数+正则化得到的函数)的最优解,而不是损失函数的最优解。
正则项就是为了防止达到损失达到损失函数最优而导致的过拟合,所以正则项能把最优解往外拉。
并且,换个角度理解,越接近loss函数的最优点,代表模型复杂度越高,拟合程度越大,当引入惩罚项来拉动远离最低点,就使得模型复杂度越低,模型容量更小,可以防止过拟合。
至于为什么是两个函数曲线相切的点呢?
答: 因为两个曲线相切时,黄线和绿线梯度一样,并且由于二者梯度方向相反,此时梯度绝对值最小为0,参数就不会再更新下去了,得到了平衡,也就得到了最优解。
4. 参数更新法则

所以,新的更新梯度,每次是wt乘以一个小于1的数,再沿着梯度的反方向走一点。
为什么叫权重衰退?
答:是因为λ的引入,使得在更新参数前,把当前的权重进行了一次缩小(一次衰退)。
5. 总结
- 权重衰退通过L2正则项使得模型参数不会过大,从而控制模型复杂度
- 正则项权重是控制模型复杂度的超参数
6. 一些Q&A
- 为什么参数选择范围小,模型复杂度就更低了呢?
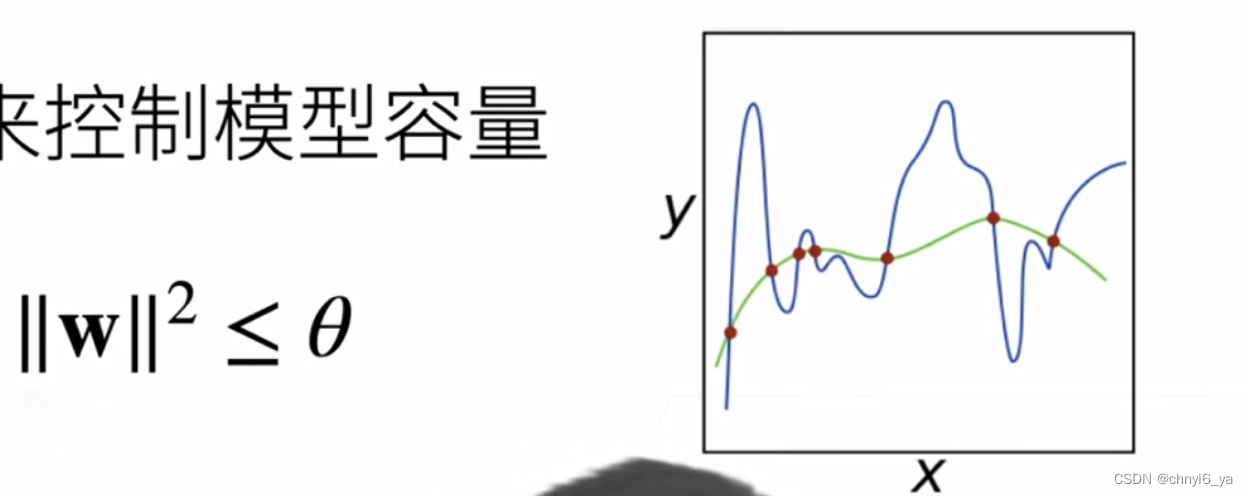
答:以上图中的函数图像来说,要去拟合那些红点,如果可以允许模型参数选的比较大的话,可以做一个任何一个很复杂的曲线(如蓝色曲线)去拟合。
比如说,同样是二次模型或者三次模型这种简单模型,假设我的权重可以取到很大,会造成一个非常不平滑的曲线。那现在限制w的取值范围,也就是只能去学习比较平滑的曲线,而不去学复杂的曲线,就意味着模型复杂度变低。
或者这么理解,一个多项式中的高次项的系数变小了或者为0,函数也就变平滑了。