哈希表与布隆过滤器

news2025/1/13 17:33:13

文章目录

  • 一、哈希函数是什么？
    • 哈希函数的应用场景
    • 哈希函数的构造方法
  • 二、哈希表
      • 哈希表的底层设计
      • 题型
  • 三、布隆过滤器
      • 布隆过滤器优点
      • 布隆过滤器缺陷
      • 布隆过滤器使用场景
    • 一致性哈希算法.
    • 位图
  • 3. 海量数据面试题

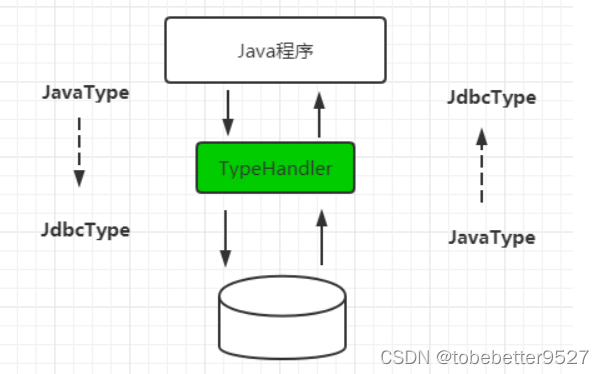
一、哈希函数是什么？

1 : 哈希函数没有随机值
2 : 理论上的哈希碰撞是不可避免的(因为,输入域无限,输出域有限)
3 : 哈希函数具有离散性和均匀性

离散型指 : 即使是有规律的数字算出来的结果也是大不相同的
均匀性指 : 哈希函数算出来的结果总是均匀分布在输出 域中

哈希函数的应用场景

1:对主要操作是查找
2:对数据没有逻辑上的要求
3:先让数据均匀分配

哈希函数的构造方法

掌握常用的俩种就行

  1. 直接定制法-
    取关键字的某个线性函数为散列地址：Hash（Key）= A*Key + B 优点：简单、均匀 缺点：需要事先知道关
    键字的分布情况 使用场景：适合查找比较小且连续的情况 面试题：字符串中第一个只出现一次字符
  2. 除留余数法–
    设散列表中允许的地址数为m，取一个不大于m，但最接近或者等于m的质数p作为除数，按照哈希函数：
    Hash(key) = key% p(p<=m),将关键码转换成哈希地址

二、哈希表

哈希表,就是一种运用哈希函数的数据结构
哈希表空间的使用-只和输入不同的数有关
哈希表在使用上是可以认为O(1)的但不是理论上-理论上就是logN的

哈希表的底层设计

给定一个输出域,通过哈希函数算出一个值,模一个值给定到输出域中,然后后来来的值以单链表的形式加到这个值的后面.
如果这个单链表的值的数量过大了,那就的扩容.也就是将原来的哈希表中的每一个值,重新算一遍哈希模一个新值,然后在以链表形式串起来.

哈希表查找和删除为什么是O(1),因为通过哈希函数算肯定是O(1)的(即使是这个时间长),而通过单链表查询的话(如果这个单链表很短,那么也认为是O(1),单链表长度一旦过长就出发扩容操作)
扩容的时间复杂度怎么算 ,假设一次扩容一倍,时间复杂度就是logN,那么总的给定N个数的时间复杂度O(NlogN),而单次扩容的时间复杂度O(NlogN) / N = logN 这是一个小常数,而且这个哈希表不一定一次只扩容1倍,那么通过增加扩容的数量,这个logK会更小,可以认为单次的logK = O(1)
而且Java有一种技术就是离线扩容技术,可以进一步加速这个时间复杂度(C++没有)
因为Java有jvm会保存哈希表,所以Java可以一边扩容一边使用老的哈希表,等新表扩容(不占用用户时间)完,在释放旧表使用新表

题型

1:如果给定你1G的内存,给你40亿的数,要求里找出出现次数最多的数
解题思路:
首先经典解题思路,就是将所有数都加入到哈希表中然后去找,但是内存肯定会爆掉
怎样设计,就是将40亿的数都算一遍哈希值,然后模个100,放到0-99的文件(这些文件肯定是能放到内存中的)中,然后在这些文件中找出现次数最多的数,然后比较所有文件中出现次数最多的数.

原理:就是哈希相同的值一定会算到同一个文件中,不同的数会根据离散型均匀的分配到文件中.

2 : 哈希表题:设计一个哈希表,能够随机的返回哈希表中的每一个值
在这里插入图片描述

 //实现哈希随机
    public static class Pool<K>{
        private HashMap<K,Integer> keyIndexMap;
        private HashMap<Integer,K> indexKeyMap;
        private int size;

        public Pool(){
            this.keyIndexMap = new HashMap<>();
            this.indexKeyMap = new HashMap<>();
            this.size = 0;
        }
        public void insert(K key){
            if (!keyIndexMap.containsKey(key)){
                this.keyIndexMap.put(key,size);
                this.indexKeyMap.put(size++,key);
            }
        }
        public void delete(K key){
            if (keyIndexMap.containsKey(key)){
                //记录位置,然后堵洞
                int deleteIndex = keyIndexMap.get(key);
                //将最后一个位置拿出来
                int lastIndex = --size;
                K lastKey = indexKeyMap.get(lastIndex);
                //堵洞交换
                keyIndexMap.put(lastKey,deleteIndex);
                indexKeyMap.put(deleteIndex,lastKey);
                keyIndexMap.remove(key);
                indexKeyMap.remove(lastIndex);
            }
        }
        public K getRondom(){
            if (size == 0)return null;
            int randomIndex =(int) (Math.random()*size);//0 ~ size -1
            return indexKeyMap.get(randomIndex);
        }
    }

三、布隆过滤器

布隆过滤器是由布隆（Burton Howard Bloom）在1970年提出的 一种紧凑型的、比较巧妙的概率型数据结构，特点是高效地插入和查询，可以用来告诉你 “某样东西一定不存在或者可能存在”，它是用多个哈希函数，将一个数据映射到位图结构中。此种方式不仅可以提升查询效率，也可以节省大量的内存空间

解决,类似于黑名单查找的问题(爬虫行为)-没有删除行为,允许一定的失误率(失误率很低)

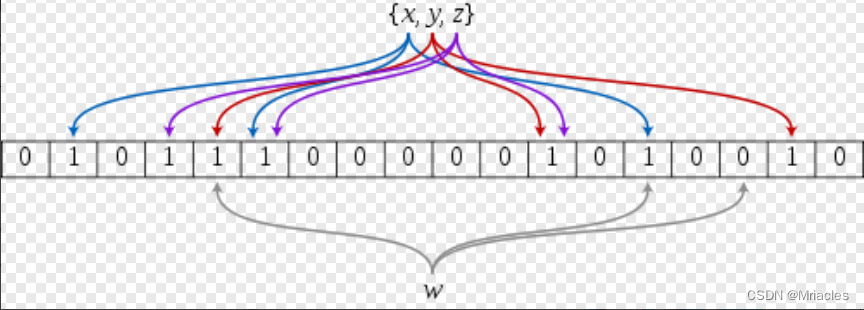
在这里插入图片描述

失误率:假如一个号是黑号,那么这个黑号一定能被查找到,但是也允许一定的白号但是被误杀了

布隆过滤器是哈希表和位图的结合
先将字符串用字符串哈希算法映射到哈希表中
但是由于哈希冲突，我们可以把一个字符串用多个不同的字符串哈希算法同时映射在整个哈希表中
要判断一个字符串是否在这堆字符串中，我们可以算出这个字符串的位置,当且仅当这个字符串每个映射位置都是1的时候才表示存在，只要有一个位置为0，就表示不存在

俩个问题:用多少个哈希函数,位图到底定多大(m)
哈希函数:根据样本量和位图大小来订(类似于猜指纹,不能太多要不位图全部被填满了,太少可能不准确)

三个公式
在这里插入图片描述

package bloomfilterdemo;

import java.util.BitSet;

/**
 * @Author 12629
 * @Description：
 */
class SimpleHash {

    public int cap;//当前容量
    public int seed;//随机

    public SimpleHash(int cap,int seed) {
        this.cap = cap;
        this.seed = seed;
    }

    //根据seed不同 创建不能的哈希函数
    int hash(String key) {
        int h;
        //(n - 1) & hash
        return (key == null) ? 0 : (seed * (cap-1)) & ((h = key.hashCode()) ^ (h >>> 16));
    }

}
public class MyBloomFilter {

    public static final int DEFAULT_SIZE = 1 << 20;
    //位图
    public BitSet bitSet;
    //记录存了多少个数据
    public int usedSize;

    public static final int[] seeds = {5,7,11,13,27,33};

    public SimpleHash[] simpleHashes;

    public MyBloomFilter() {
        bitSet = new BitSet(DEFAULT_SIZE);
        simpleHashes = new SimpleHash[seeds.length];
        for (int i = 0; i < simpleHashes.length; i++) {
            simpleHashes[i] = new SimpleHash(DEFAULT_SIZE,seeds[i]);
        }
    }

    /**
     * 添加元素 到布隆过滤器
     * @param val
     */
    public void add(String val) {
        //让X个哈希函数  分别处理当前的数据
        for (SimpleHash simpleHash : simpleHashes) {
            int index = simpleHash.hash(val);
            //把他们 都存储在位图当中即可
            bitSet.set(index);
        }
    }
    /**
     * 是否包含val ，这里会存在一定的误判的
     * @param val
     * @return
     */
    public boolean contains(String val) {
        //val  一定 也是通过这个几个哈希函数去 看对应的位置
        for (SimpleHash simpleHash : simpleHashes) {
            int index = simpleHash.hash(val);
            //只要有1个为 0     那么一定不存在
            boolean flg = bitSet.get(index);
            if(!flg) {
                return false;
            }
        }
        return true;
    }

    public static void main(String[] args) {
        MyBloomFilter myBloomFilter = new MyBloomFilter();
        myBloomFilter.add("hello");
        myBloomFilter.add("hello2");
        myBloomFilter.add("bit");
        myBloomFilter.add("haha");

        System.out.println(myBloomFilter.contains("hello"));
        System.out.println(myBloomFilter.contains("hello3"));
        System.out.println(myBloomFilter.contains("he"));
    }
}

模拟实现2

import java.util.BitSet;
	// 构建哈希函数
	class SimpleHash {
	//容量
		private int cap;
		//随机种子
		private int seed;
		public SimpleHash( int cap, int seed) {
		this.cap= cap;
		this.seed =seed;
	}
	/**
	* 把当前的字符串转变为1个哈希值
	* @param value
	* @return
	*/
	public int hash(String value) {
		int result=0 ;
		
		int len= value.length();
		for (int i= 0 ; i< len; i ++ ) {
			result = seed* result + value.charAt(i);
		}
		return (cap - 1 ) & result;
		}
	}
	public class BloomFilter {
		private static final int DEFAULT_SIZE = 1 << 24 ;//方便哈希函数的计算
		private static final int [] seeds = new int []{5,7, 11 , 13 , 31 , 37 , 61};
		private BitSet bits; // 位图用来存储元素
		private SimpleHash[] func; // 哈希函数所对应类
		private int size = 0;
		//初始化bits和func
		public BloomFilter() {
		bits= new BitSet(DEFAULT_SIZE);
		func = new SimpleHash[seeds.length];
		//把所有哈希对象进行初始化
		for( int i= 0 ; i< seeds.length; i ++ ) {
			func[i]=new SimpleHash(DEFAULT_SIZE, seeds[i]);
		}
	}
	public void set(String value) {
		if(null == value)
		return;
		for(SimpleHash f : func) {
			bits.set(f.hash(value));
		}
		size++;
	}
	public boolean contains(String value) {
		if(value ==null ) {
			return false;
		}
		for(SimpleHash f : func) {
			if(!bits.get(f.hash(value))){
				return false;
			}
		}
		return true;//会有误判
	}
	public static void main(String[] args) {
		String s1 = "欧阳锋";
		String s2 = "欧阳克";
		
		String s3 = "金轮法王";
		String s4 = "霍都";
		BloomFilter filter=new BloomFilter();
		filter.set(s1);
		filter.set(s2);
		filter.set(s3);
		filter.set(s4);
		System.out.println(filter.contains("杨过"));
		System.out.println(filter.contains("金轮法王"));
	}
}

布隆过滤器优点

  1. 增加和查询元素的时间复杂度为:O(K), (K为哈希函数的个数，一般比较小)，与数据量大小无关
  2. 哈希函数相互之间没有关系，方便硬件并行运算
  3. 布隆过滤器不需要存储元素本身，在某些对保密要求比较严格的场合有很大优势
  4. 在能够承受一定的误判时，布隆过滤器比其他数据结构有这很大的空间优势
  5. 数据量很大时，布隆过滤器可以表示全集，其他数据结构不能
  6. 使用同一组散列函数的布隆过滤器可以进行交、并、差运算

布隆过滤器缺陷

  1. 有误判率，即存在假阳性(False Position)，即不能准确判断元素是否在集合中(补救方法：再建立一个白
    名单，存储可能会误判的数据)
  2. 不能获取元素本身
  3. 一般情况下不能从布隆过滤器中删除元素
  4. 如果采用计数方式删除，可能会存在计数回绕问题

布隆过滤器使用场景

  1. google的guava包中有对Bloom Filter的实现
  2. 网页爬虫对URL的去重，避免爬去相同的URL地址。
  3. 垃圾邮件过滤，从数十亿个垃圾邮件列表中判断某邮箱是否是垃圾邮箱
  4. 解决数据库缓存击穿，黑客攻击服务器时，会构建大量不存在于缓存中的key向服务器发起请求，在数
    据量足够大的时候，频繁的数据库查询会导致挂机。
  5. 秒杀系统，查看用户是否重复购买

一致性哈希算法.

这里不写了,看下这篇博客

https://zhuanlan.zhihu.com/p/129049724

在这里插入图片描述

位图

所谓位图，就是用每一位来存放某种状态，适用于海量数据，整数，数据无重复的场景。通常是用来判断某个数据存不存在的

用来快速判断一个整数是否在一堆整数中

二进制用0和1来表示数据，位图根据0和1来存储对应的数据，可以大大节省存储空间，并具备排序特性。

public static void main(String[] args) {
        int a =0;// a 32 bit
        int [] arr =new int[10];// 32*10 -> 320bits数组
        /* arr [0] int 0 - 31
        *  arr [1] int 32 - 63 */
        int i =178;//想取第178个bit 状态

        int numIndex = 178/32;//找到178所在的数字
        int bitIndex = 178%32;//找到178所在数字中的位数

        //拿到178位的状态
        int s = (   (arr[numIndex] >> (bitIndex))       & 1);

        //将178位的状态改成 1
        arr[numIndex] = arr[numIndex] | ( 1 << (bitIndex) );


        //将178位的状态改成 0
        arr[numIndex] = arr[numIndex] & ( ~ 1 << (bitIndex) );

    }

public class MyBitSet {
	private byte[] elem;
	public int usedSize;
	public MyBitSet() {
	//默认只给一个大小
		elem = new byte[1];
	}
	/**
	* n个比特位
	* @param n
	*/
	public MyBitSet(int n) {
		elem = new byte[n/8+1];
	}
	/**
	*
	* @param val 可以等价于 将数据的对应位置置为1
	*/
	public void set(int val) {
		if(val < 0 ) {
			throw new IndexOutOfBoundsException();
		}
		int arrayIndex = val/8;
		int bitIndex = val % 8;
		this.elem[arrayIndex] |= (1 << bitIndex);
		usedSize++;
	}
	/**
	* 测试该数字是否存在
	* @param val
	* @return
	*/
	public boolean get(int val) {
		if(val < 0 ) {
			throw new IndexOutOfBoundsException();
		}
		int arrayIndex = val/8;
		int bitIndex = val % 8;
		//判断 elem[index] 的对应位是不是1 是的话与的结果是不等于0的
		if((this.elem[arrayIndex] & (1L << bitIndex)) != 0) {
		return true;
	}
	
	return false;
	}
	/**
	*
	* @param val 可以等价于 将数据的对应位置置为0
	*/
	public void reSet(int val) {
		if(val < 0 ) {
			throw new IndexOutOfBoundsException();
		}
		int arrayIndex = val/8;
		int bitIndex = val % 8;
		this.elem[arrayIndex] &= ~(1L << bitIndex);
		usedSize--;
	}
	/**
	* 当前比特位有多少个1
	* @return
	*/
	public int getUsedSize() {
		return this.usedSize;
	}
}

3. 海量数据面试题

哈希切割
给一个超过100G大小的log file, log中存着IP地址, 设计算法找到出现次数最多的IP地址？ 与上题条件相同，
如何找到top K的IP？
位图应用

  1. 给定100亿个整数，设计算法找到只出现一次的整数？
  2. 给两个文件，分别有100亿个整数，我们只有1G内存，如何找到两个文件交集？
  3. 位图应用变形：1个文件有100亿个int，1G内存，设计算法找到出现次数不超过2次的所有整数
    布隆过滤器
  4. 给两个文件，分别有100亿个query，我们只有1G内存，如何找到两个文件交集？分别给出精确算法和
    近似算法
  5. 如何扩展BloomFilter使得它支持删除元素的操作

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/794574.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

二.安装helm

二.安装helm

1.什么是helm Kubernetes 包管理器 Helm 是查找、分享和使用软件构件 Kubernetes 的最优方式。 Helm 管理名为 chart 的 Kubernetes 包的工具。Helm 可以做以下的事情&#xff1a; 从头开始创建新的 chart将 chart 打包成归档(tgz)文件与存储 chart 的仓库进行交互在现有的 K…
阅读更多...
【数据结构】_4.List接口实现类LinkedList与链表

【数据结构】_4.List接口实现类LinkedList与链表

目录 1.链表的结构与特点 1.1 链表的结构&#xff1a; 1.2 链表的特点&#xff1a; 2. 不带头单链表的模拟实现 3. 单链表OJ 3.1 题目1&#xff1a;移除链表元素: 3.2 题目2&#xff1a;反转一个单链表 3.3 题目3&#xff1a;返回链表的中间结点 3.4 题目4&#xff1…
阅读更多...
Python连接MariaDB数据库

Python连接MariaDB数据库

Python连接MariaDB数据库 一、安装mariadb库 pip install mariadb 二、连接数据库 connect()函数连接数据库。 import mariadbconn mariadb.connect(user"root", password"Root123", host"192.168.0.182", port3306, database"compan…
阅读更多...
Linux环境搭建（XShell+云服务器）

Linux环境搭建（XShell+云服务器）

好久不见啊&#xff0c;放假也有一周左右了&#xff0c;简单休息了下&#xff08;就是玩了几天~~&#xff09;&#xff0c;最近也是在学习Linux&#xff0c;现在正在初步的学习阶段&#xff0c;本篇将会简单的介绍一下Linux操作系统和介绍Linux环境的安装与配置&#xff0c;来帮…
阅读更多...
【沁恒蓝牙mesh】组网方式选择与分析

【沁恒蓝牙mesh】组网方式选择与分析

本文主要介绍了【沁恒蓝牙mesh】组网方式选择与分析 1.开发环境搭建与程序烧录 参考博文&#xff1a;【经验】如何搭建沁恒蓝牙SoC CH58x开发环境 2. 组网方式 蓝牙mesh组网实践&#xff08;配网方式的选择&#xff09; 自配网&#xff1a;自己给自己配网&#xff0c;当节点…
阅读更多...
Labview串口通信MSComm实现串口收发

Labview串口通信MSComm实现串口收发

文章目录 前言一、什么是 MSComm二、MSComm 控件下载三、MSComm 控件的注册四、使用 MSComm 控件1、前面板放置控件2、MSComm 的常用属性3、MSComm 控件的事件 五、实现串口收发1、搭建虚拟串口2、发送测试3、接收测试4、后面板核心程序框图 六、程序自取 前言 本文介绍使用 A…
阅读更多...
study 第三方库

study 第三方库

import osprint(os.listdir()) #列出当前目录下的文件 print(os.getcwd()) #获取绝对路径if not os.path.exists("b"):os.mkdir("b") if not os.path.exists("b/test.ext"):f open("b/text.txt","w")f.write("hello,f…
阅读更多...
sql学习笔记

sql学习笔记

sql语句优先级 FROM → WHERE → GROUP BY → SELECT → HAVING → ORDER BY sql case用法 例题&#xff1a; 按照销售单价( sale_price )对练习 3.6 中的 product&#xff08;商品&#xff09;表中的商品进行如下分类。 低档商品&#xff1a;销售单价在1000日元以下&#x…
阅读更多...
MATLAB | 产生阿尔法稳定分布噪声并作出概率密度函数

MATLAB | 产生阿尔法稳定分布噪声并作出概率密度函数

一、问题描述 想产生不同特征参数的α稳定随机变量&#xff0c;并且作出其概率密度函数进行对比。 二、解决思路 运行了MATLAB的官方实例代码&#xff1a; openExample(‘stats/ComparePDFsOfStableDistributionsExample’) &#xff08;1&#xff09;使用makedist()函数生成…
阅读更多...
低代码未来的发展方向

低代码未来的发展方向

大的未来都是AI &#xff0c;AI &#xff0c; AI …&#xff0c;理论上不可能有别的。 拿iVX来说吧&#xff0c;已经做了一整套完整的 可视化编程范式&#xff0c;基本可以生成所有系统的前端后台和数据库代码。也就是说&#xff0c;其组件系统和逻辑表达&#xff08;非代码&a…
阅读更多...
整天用 Calendar 日历组件，不如自己手写一个吧！

整天用 Calendar 日历组件，不如自己手写一个吧！

目录 Date 的 api 实现日历组件 静态的布局 再来写逻辑 增加两个参数 提供 ref 来暴露 api 总结 日历组件想必大家都用过&#xff0c;在各个组件库里都有。比如 antd 的 Calendar 组件&#xff08;或者 DatePicker 组件&#xff09;&#xff1a; 那这种日历组件是怎么实…
阅读更多...
【论文阅读】A Comprehensive Survey

【论文阅读】A Comprehensive Survey

论文来源&#xff1a;Li M , Liu Y , Liu X ,et al.The Deep Learning Compiler: A Comprehensive Survey[J]. 2020.DOI:10.1109/TPDS.2020.3030548. 这是一篇关于深度学习编译器的综述类文章。 什么是深度学习编译器 深度学习&#xff08;Deep Learning&#xff09;编译器将…
阅读更多...
STM32H5开发(4)----开发板介绍

STM32H5开发(4)----开发板介绍

STM32H5开发----4.开发板介绍 套件概述样品申请特征系统控制和生态系统访问功能示意图系统框图跳线设置开发板原理图 套件概述 STM32H503RBTx_LQFP64是STM32H5系列微控制器的一款出色评估套件&#xff0c;它采用了先进的40nm工艺制造&#xff0c;为开发者提供了卓越的性能和能…
阅读更多...
MyBatis基础模块-类型转换模块

MyBatis基础模块-类型转换模块

文章目录 1. 为什么需要类型转换模块2. TypeHandler 1. 为什么需要类型转换模块 执行sql&#xff0c;在PreparedStatement设置参数时&#xff0c;需要把java类型转换成jdbc类型&#xff0c;而从结果集中获取数据时&#xff0c;需要把jdbc类型转换为java类型。 2. TypeHandle…
阅读更多...
软件测试未来的发展趋势以及软件测试进阶路线

软件测试未来的发展趋势以及软件测试进阶路线

全球各地的企业每天都在发展变化着&#xff0c;以应对市场挑战&#xff0c;满足日益成熟的客户需求。即使是正在进行的技术进步也会使软件测试专家在实践的过程中更加专注和精确。 2021年给软件测试领域带来了新的技术解决方案&#xff0c;以及质量保证和软件测试的实现。与此同…
阅读更多...
【数据结构和算法14】堆结构（基于数组实现）

【数据结构和算法14】堆结构（基于数组实现）

目录 1、有关二叉树和堆的介绍 2、大根堆的代码实现 3、小根堆的代码实现 1、有关二叉树和堆的介绍 计算机科学中&#xff0c;堆是一种基于树的数据结构&#xff0c;通常用完全二叉树实现。堆的特性如下 在大顶堆&#xff08;大根堆&#xff09;中&#xff0c;任意节点 C 与…
阅读更多...
开源视频监控管理平台国标GB28181视频EasyCVR电子地图功能展示优化

开源视频监控管理平台国标GB28181视频EasyCVR电子地图功能展示优化

视频监控综合管理平台EasyCVR可提供的视频能力包括&#xff1a;视频监控直播、云端录像、云存储、录像检索与回看、告警上报、平台级联、云台控制、语音对讲、电子地图、H.265自动转码等&#xff0c;也具备接入AI智能分析的能力。 视频汇聚平台EasyCVR可拓展性强、视频能力灵活…
阅读更多...
centos7中用shell脚本实现mysql分库分表备份

centos7中用shell脚本实现mysql分库分表备份

环境&#xff1a; 脚本&#xff1a; #!/bash/bin back_path/backup/db databases_file/backup/databases.list [ -f $databases_file ] || touch /backup/databases.list if [[ ! -s ${databases_file} ]] thenecho "$databases_file为空,请在该文件中写上需要备份的数据…
阅读更多...
C# Modbus TCP上位机测试

C# Modbus TCP上位机测试

前面说了三菱和西门子PLC的上位机通信&#xff0c;实际在生产应用中&#xff0c;设备会有很多不同的厂家生产的PLC&#xff0c;那么&#xff0c;我们就需要一种通用的语言&#xff0c;进行设备之间的通信&#xff0c;工业上较为广泛使用的语言之一就是Modbus。 Modbus有多种连…
阅读更多...
filscan api 获取错误扇区个数

filscan api 获取错误扇区个数

获取错误扇区个数 POST 请求 curl -s -X POST -H "Content-Type: application/json" -d {"account_id": "f01889512"} https://api-v2.filscan.io/api/v1/AccountInfoByID | jq -r .result.account_info.account_miner.account_indicator.fault…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023