目录
1、有关二叉树和堆的介绍
2、大根堆的代码实现
3、小根堆的代码实现
1、有关二叉树和堆的介绍
计算机科学中,堆是一种基于树的数据结构,通常用完全二叉树实现。堆的特性如下
-
在大顶堆(大根堆)中,任意节点 C 与它的父节点 P 符合 P.value >= C.value
-
而小顶堆(小根堆)中,任意节点 C 与它的父节点 P 符合 P.value <= C.value
-
最顶层的节点(没有父亲)称之为 root 根节点
例1 - 满二叉树(Full Binary Tree)特点:每一层都是填满的

例2 - 完全二叉树(Complete Binary Tree)特点:最后一层可能未填满,靠左对齐
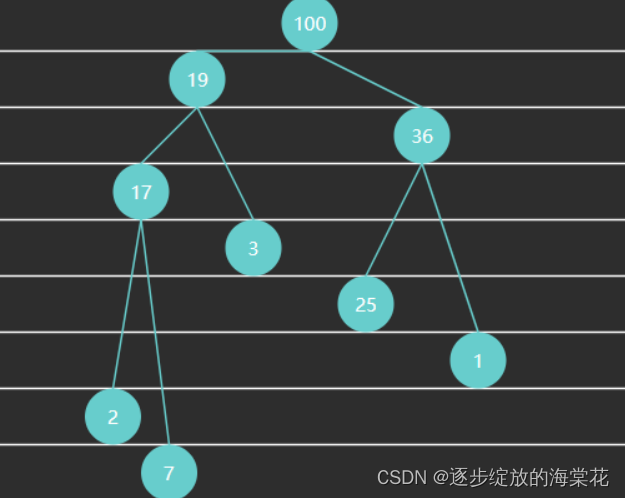
例3 - 大根堆
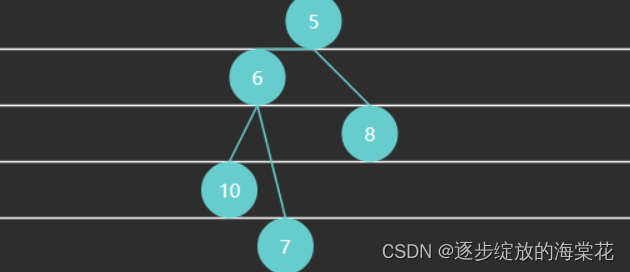
例4 - 小根堆
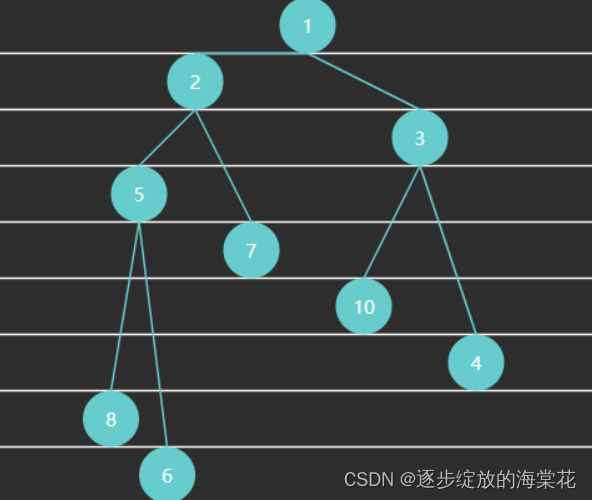
完全二叉树可以使用数组来表示
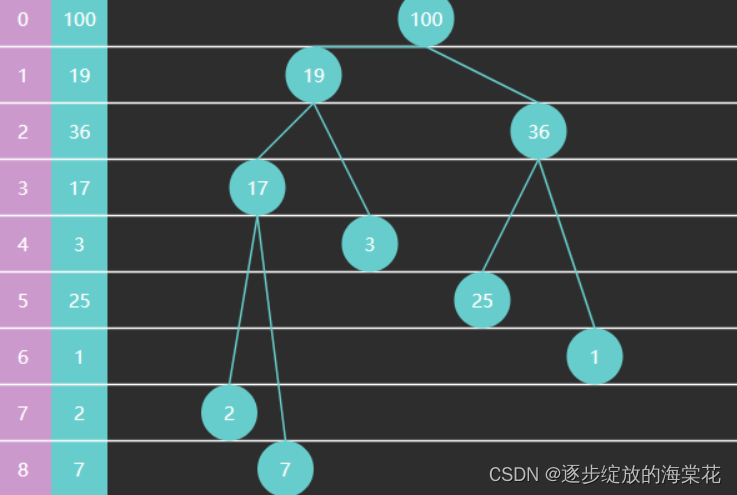
-
如果从索引 0 开始存储节点数据
-
节点 i 的父节点为 floor((i-1)/2),当 i>0 时
-
节点 i 的左子节点为 2i+1,右子节点为 2i+2,当然它们得 < size
-
-
如果从索引 1 开始存储节点数据
-
节点 i 的父节点为 floor(i/2),当 i > 1 时
-
节点 i 的左子节点为 2i,右子节点为 2i+1,同样得 < size
-
2、大根堆的代码实现
/**
* 使用数组实现堆数据结构
* 定义一个用于存储整形数据的大根堆
*
* @author zjj_admin
*/
public class MaxHeap {
/**
* 用于存储数据
*/
private int[] array;
/**
* 堆中的数据个数
*/
private int size;
public MaxHeap(int capacity) {
this.size = 0;
this.array = new int[capacity];
//调整堆的结构
adjust();
}
/**
* 获取堆中的元素个数
*
* @return
*/
public int size() {
return size;
}
/**
* 查看堆顶元素
*
* @return
*/
public int peek() {
if (size <= 0) {
throw new NullPointerException("没有数据了");
}
return array[0];
}
/**
* 返回并移除堆顶元素
*
* @return
*/
public int poll() {
if (size <= 0) {
throw new NullPointerException("没有数据了");
}
int top = array[0];
//让第一个数据和左后一个数据做交换
exchange(0, size - 1);
size--;
// 重新对第一个元素做下潜操作
down(0);
return top;
}
/**
* 返回并移除指定索引的数据
* 1、先将索引 index 和最后一个数据进行交换
* 2、移除最后一个数据,及删除了开始索引为 index 的数据
* 3、对索引 index 的数据进行上浮操作,当不发生节点交换时再进行下潜操作
*
* @param index
* @return
*/
public int poll(int index) {
if (index < 0) {
throw new IndexOutOfBoundsException("index 必须不小于 0");
}
// 当索引数据
if (index > size - 1) {
throw new NullPointerException("没有数据了");
}
//先将索引 index 和最后一个数据进行交换
exchange(index, size - 1);
//移除最后一个数据,及删除了开始索引为 index 的数据
int removed = array[size - 1];
size--;
//对索引 index 的数据进行上浮操作,当不发生节点交换时再进行下潜操作
int newParent = up(index);
down(newParent);
return removed;
}
/**
* 向堆中添加一个元素
*
* @param value
* @return
*/
public boolean offer(int value) {
if (size >= array.length) {
return false;
}
array[size] = value;
size++;
//上浮最后一个元素
up(size - 1);
return true;
}
/**
* 调整堆结构,让其满足大根堆
* 方法:从最后一个非叶子节点开始,依次向前做下潜操作
* 在数组中,左后一个非叶子节点的索引为:(size/2 - 1)
*/
private void adjust() {
for (int i = size / 2 - 1; i >= 0; i--) {
//依次做下潜操作即可
down(i);
}
}
/**
* 堆节点做下潜操作,让父节点数据不小于子节点数据
*
* @param parent
*/
private void down(int parent) {
if (2 * parent + 1 < size && array[parent] < array[2 * parent + 1]) {
// 交换位置
exchange(parent, 2 * parent + 1);
// 做下潜操作
down(2 * parent + 1);
} else if (2 * parent + 2 < size && array[parent] < array[2 * parent + 2]) {
// 交换位置
exchange(parent, 2 * parent + 2);
// 做下潜操作
down(2 * parent + 2);
}
}
/**
* 上浮操作,并返回上浮终点索引
*
* @param child
* @return 上浮终点索引
*/
private int up(int child) {
int parent = (child - 1) / 2;
while (parent >= 0 && array[child] > array[parent]) {
exchange(parent, child);
child = parent;
parent = (child - 1) / 2;
}
return Math.max(child, 0);
}
/**
* 交换堆中两个位置的数据
*
* @param i
* @param j
*/
private void exchange(int i, int j) {
int temp = array[i];
array[i] = array[j];
array[j] = temp;
}
@Override
public String toString() {
int[] a = new int[size];
System.arraycopy(array, 0, a, 0, size);
return Arrays.toString(a);
}
}3、小根堆的代码实现
/**
* 使用数组实现堆数据结构
*
* @author zjj_admin
*/
public class MinHeap {
/**
* 用于存储数据
*/
private int[] array;
/**
* 堆中的数据个数
*/
private int size;
public MinHeap(int capacity) {
this.size = 0;
this.array = new int[capacity];
//调整堆的结构
adjust();
}
/**
* 获取堆中的元素个数
*
* @return
*/
public int size() {
return size;
}
/**
* 查看堆顶元素
*
* @return
*/
public int peek() {
if (size <= 0) {
throw new NullPointerException("没有数据了");
}
return array[0];
}
/**
* 返回并移除堆顶元素
*
* @return
*/
public int poll() {
if (size <= 0) {
throw new NullPointerException("没有数据了");
}
int top = array[0];
//让第一个数据和左后一个数据做交换
exchange(0, size - 1);
size--;
// 重新对第一个元素做下潜操作
down(0);
return top;
}
/**
* 返回并移除指定索引的数据
* 1、先将索引 index 和最后一个数据进行交换
* 2、移除最后一个数据,及删除了开始索引为 index 的数据
* 3、对索引 index 的数据进行上浮操作,当不发生节点交换时再进行下潜操作
*
* @param index
* @return
*/
public int poll(int index) {
if (index < 0) {
throw new IndexOutOfBoundsException("index 必须不小于 0");
}
// 当索引数据
if (index > size - 1) {
throw new NullPointerException("没有数据了");
}
//先将索引 index 和最后一个数据进行交换
exchange(index, size - 1);
//移除最后一个数据,及删除了开始索引为 index 的数据
int removed = array[size - 1];
size--;
//对索引 index 的数据进行上浮操作,当不发生节点交换时再进行下潜操作
int newParent = up(index);
down(newParent);
return removed;
}
/**
* 向堆中添加一个元素
*
* @param value
* @return
*/
public boolean offer(int value) {
if (size >= array.length) {
return false;
}
array[size] = value;
size++;
//上浮最后一个元素
up(size - 1);
return true;
}
/**
* 调整堆结构,让其满足大根堆
* 方法:从最后一个非叶子节点开始,依次向前做下潜操作
* 在数组中,左后一个非叶子节点的索引为:(size/2 - 1)
*/
private void adjust() {
for (int i = size / 2 - 1; i >= 0; i--) {
//依次做下潜操作即可
down(i);
}
}
/**
* 堆节点做下潜操作
*
* @param parent
*/
private void down(int parent) {
if (2 * parent + 1 < size && array[parent] > array[2 * parent + 1]) {
// 交换位置
exchange(parent, 2 * parent + 1);
// 做下潜操作
down(2 * parent + 1);
} else if (2 * parent + 2 < size && array[parent] > array[2 * parent + 2]) {
// 交换位置
exchange(parent, 2 * parent + 2);
// 做下潜操作
down(2 * parent + 2);
}
}
/**
* 上浮操作,并返回上浮终点索引
*
* @param child
* @return 上浮终点索引
*/
private int up(int child) {
int parent = (child - 1) / 2;
while (parent >= 0 && array[child] < array[parent]) {
exchange(parent, child);
child = parent;
parent = (child - 1) / 2;
}
return Math.max(child, 0);
}
/**
* 交换堆中两个位置的数据
*
* @param i
* @param j
*/
private void exchange(int i, int j) {
int temp = array[i];
array[i] = array[j];
array[j] = temp;
}
@Override
public String toString() {
int[] a = new int[size];
System.arraycopy(array, 0, a, 0, size);
return Arrays.toString(a);
}
}