一、翻转二叉树

使用前、后序反转最为方便。

// 使用递归三部曲
class Solution
{
public:
    TreeNode *dfs(TreeNode *root)
    {
        // 前序反转
        if (root == nullptr)
            return root;
        swap(root->left, root->right);
        dfs(root->left);
        dfs(root->right);
        return root;
    }
    TreeNode *invertTree(TreeNode *root)
    {
        dfs(root);
        return root;
    }
};

为啥不推荐中序？

中序遍历，某些节点的左右孩子会翻转两次，某些节点左右孩子不会被反转。

二、对称二叉树

101.对称二叉树
关键在于，看这个节点对应的左子树和右子树是否可以相互反转。

1、如何比较呢？

比较的是两个子树的里侧和外侧的元素是否相等。

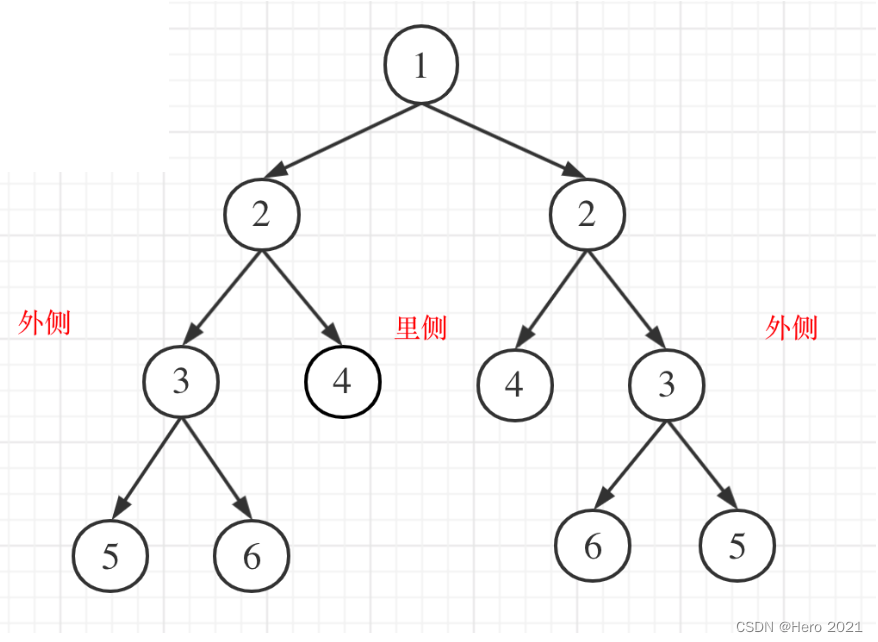
2、确定遍历顺序?

使用后续！(左 右 根)

3、为啥使用后续呢？

因为要把左右孩子的信息返回给根节点，这样才能判断是否能够反转。

确定递归函数的参数和返回值：

 bool compare(TreeNode* left,TreeNode* right)

终止条件：

bool compare(TreeNode *left, TreeNode *right)
{
    if (left != nullptr && right == nullptr)
        return false;
    else if (left == nullptr && right != nullptr)
        return false;
    else if (left == nullptr && right == nullptr)
        return true;
    else if (left->val != right->val)
        return false;

	else ...
}

单层递归逻辑：

// 单层递归逻辑
bool outside = compare(left->left, right->right);
bool inside = compare(left->right, right->left);
bool res = outside && inside;                   
return res;

完整代码：

class Solution
{
public:
    bool compare(TreeNode *left, TreeNode *right)
    {
        if (left != nullptr && right == nullptr)
            return false;
        else if (left == nullptr && right != nullptr)
            return false;
        else if (left == nullptr && right == nullptr)
            return true;
        else if (left->val != right->val)
            return false;

        // 单层递归逻辑
        bool outside = compare(left->left, right->right); // 左 右
        bool inside = compare(left->right, right->left);  // 右 左
        bool res = outside && inside;                     // 根 根
        return res;
    }
    bool isSymmetric(TreeNode *root)
    {
        if (root == nullptr)
            return true;
        return compare(root->left, root->right);
    }
};