解决链表环入口问题
文章目录
- 解决链表环入口问题
- 前言
- 链表中环的问题
- Hash和集合的解法:
- 快慢指针实现解决:
- 解题思路:
- Hash或者使用集合的方式实现
- 快慢指针(这里使用三次刚好解决)
- 总结
前言
提示:无论今天过得如何,就当穿了一天的袜子,回家就脱了吧。
当然解决这个问题之前,我们需要了解一个概念,就是链表的有环是怎么判断的,定义是什么?
废话不多说,直接上图片💕
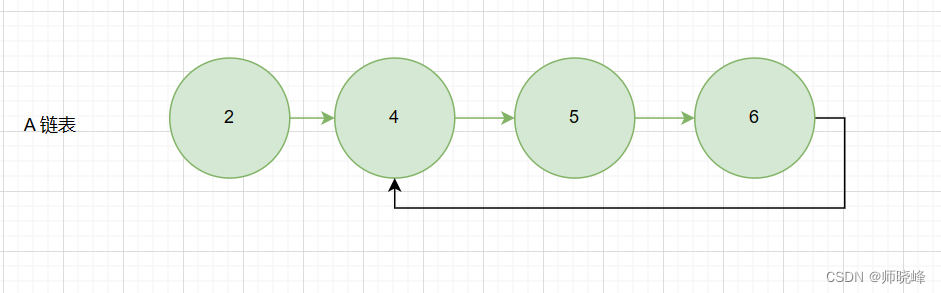
在这个A链表中,我们就看出他是存在环的
- 有环
- 节点 4 就是环的入口
这就引出来另一个问题了,怎么判断链表有环❔
链表中环的问题
当然拿到这个问题,思考的话(最快想到的解决方法就是Hash[map]),下来就是采用集合呗🥰,虽然这样的话可以很快解决,有点儿逃避链表的嫌疑😒
Hash和集合的解法:
遍历链表,一次将数据元素存入map中,是要是发现有相同的元素,就说明链表中有环,代码实现起来也很简单。
/**
* 方法1:通过HashMap判断
*
* @param head
* @return
*/
public static boolean hasCycleByMap(ListNode head) {
// 一般条件下不改变head的位置
ListNode pos = head;
HashMap<ListNode,Integer> map = new HashMap();
while(pos != null) {
if(!map.containsKey(pos)){
map.put(pos,null);
}else{
return true;
}
pos = pos.next;
}
return false;
}
使用集合的话,思想和上面👆类似,这里就不在重复了,直接上代码😂
/**
* 方法1:通过HashSet判断
*
* @param head
* @return
*/
public static boolean hasCycleByMap(ListNode head) {
// 保留一下头节点的位置
ListNode pos = head;
HashSet<ListNode> set = new HashSet<>();
while (pos != null) {
// if (set.contains(pos)){ // 这里也可以只用set判断
// return true;
// }else{
// set.add(pos);
// }
if(!set.add(pos)){
return true;
}
pos = pos.next;
}
return false;
}
那么不逃离链表,就是使用链表需要怎么解决呢?思考(三分钟💡)
常见的算法解决 双指针 呗
快慢指针实现解决:
这里快慢指针要怎么理解呢?
我们类比一个场景:就是在一个圆形的操场上跑步,一个同学跑的快,一个同学跑的慢,经过一段时间后,必然会存在两人相遇的情况,况且正好是快的同学比慢的同学多跑一圈。
这里就可以建立数学模型
- 两位通过起始地点相同 快同学 v1 慢同学 v2(目前可以这样称呼 😂起名字很纠结ahhah)
- 经过相同的时间相遇 经过时间 t
- 假设围绕操场一圈的长度是 s
s = (v1 -v2)t
这里放到链表里面就好办多了,我们就可以让fast走一步,然后fast和slow同时出发,如果后面出现fast和slow相遇,那就说明链表里面存在环呀🥰,这不就吧问题解决了。那我们就写一下代码吧。
/**
* 方法2 通过双指针实现
*
* @param head
* @return
*/
public static boolean hasCycleByTwoPoint(ListNode head) {
// 校验参数
if(head == null || head.next == null){ // 链表想要成环至少需要两个节点
return false;
}
ListNode fast = head;
ListNode slow = head;
while(fast != null && fast.next != null){ // 因为需要使用到下一个节点
fast = fast.next.next;
slow = slow.next;
if (fast == slow){
return true;
}
}
return false;
}
解题思路:
Hash或者使用集合的方式实现
最简单的办法就是Hash呗,当然使用集合也不是不行(Set)。这就不在赘述了,显得就有点啰嗦啦🤣
快慢指针(这里使用三次刚好解决)
解决了链表有环的问题,我们再来看看怎么确定链表的环形入口在哪里❔(思考一下💡)
我们再来看这个环的图:
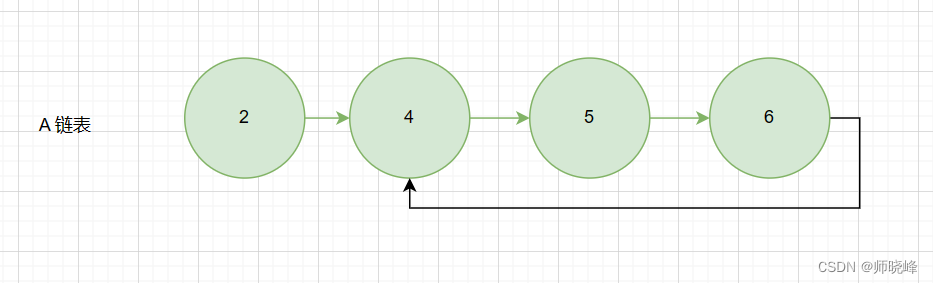
当然如果链表是这样的话也是一样的:
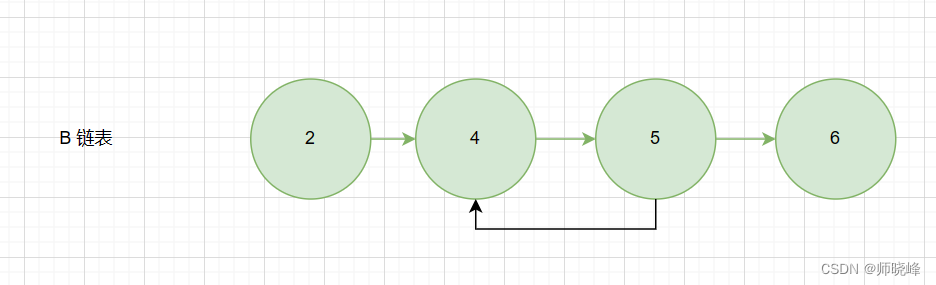
解决思路💕:
- 确定链表有环 (上面我们已经解决了)
- 确认链表的长度(这里可以相遇的时候 固定一个fast节点 让slow继续前行直到再次相遇 就可以得出环的长度 这里我们就简单的设置为 k )
- 确定环的入口(当我们从链表的后面往前看的话 链表环的入口刚好是倒数第 k 个节点。
有了思路那么实现起来就比较容易了🤩,下面就是代码的展示环节了😂
/**
* 方法2 通过双指针实现
*
* @param head
* @return
*/
public static ListNode detectCycleByTwoPoint(ListNode head) {
// 校验参数
if (head == null || head.next == null){ // 链表想要成环至少需要两个节点
return null;
}
ListNode fast = head, slow = head;
// 确定链表有环
while(fast != null && fast.next != null){
fast = fast.next.next;
slow = slow.next;
if (fast == slow){// 说明有环
// 确认链表的长度
int count = 1;
slow = slow.next;
while (fast != slow){
count++;
slow = slow.next;
}
// 确定环的入口
fast = head;
slow = head;
int temp = count;
while(temp >0){
fast = fast.next;
temp--;
}
while (count >0){
fast = fast.next;
slow = slow.next;
count--;
}
return slow;
}
}
return null;
}
总结
提示:链表环的问题是比较经典的问题,重点理解 链表环的入口问题