目录
1.帮助命令
2.数据类型
3.元胞数组和结构体
4.矩阵操作
4.1 矩阵的定义与构造
4.2 矩阵的四则运算
4.3 矩阵的下标
5.程序结构
5.1 for循环结构
5.2 分支结构
7.基本绘图操作
7.1.二维平面绘图
6.2 三维立体绘图
7.图形的保存与导出
8.补充
语句后⾯加;的作⽤是:程序运⾏时不在命令⾏窗⼝显⽰改⾏的运算结果。
format compact:%输出行间距设置为紧凑模式
format loose:%恢复到默认的松散模式
需要注意的是,
format函数的设置只会影响当前 MATLAB 会话中的输出行间距,不会改变实际的数据或变量。此外,该设置对于图形和其他非命令行的输出可能没有影响。
1.帮助命令





2.数据类型
%% 独占一行的注释
% 普通注释
clear all 删除所有变量
clc 删除命令行窗口内容
变量命名规则:区分大小写;长度不超过63
10/3=3.3333 /是真除法
abs('a') %输出97 单引号表示字符
abs('ab') %输出97 98
char(97) %输出'a'
num2str(97) %输出'a'
length('adjkasnjfka') #输出的是字符串长度
A=[1 2 3;4 5 6;7 8 9] %定义矩阵
B=A' %转置
C = A(:) %竖向拉长
D = inv(A) %逆矩阵(必须时方阵才能求逆矩阵)
A * D (相当于A×A的逆)
在MATLAB中,可以使用inv函数或者det函数来判断一个矩阵是否可逆。
·inv函数用于计算矩阵的逆。如果一个矩阵是可逆的,inv函数将返回该矩阵的逆矩阵。如果矩阵不可逆(奇异矩阵),inv函数将引发一个异常。
·det函数用于计算矩阵的行列式。如果一个矩阵的行列式不等于零,则说明该矩阵是可逆的;如果行列式等于零,则说明该矩阵是不可逆的。
E = zeros(10,5,3) 创建一个10行5列3维的全0矩阵
E(:,:,1) = rand(10,5) %rand生成均匀分布的伪随机数。分布在(0~1)之间
rand(m,n,‘double’)生成指定精度的均匀分布的伪随机数,参数还可以是’single’
rand():生成[0,1)的小数
rand(m):生成m X m的方阵,随机小数填充
rand(m,n):生成m X n的矩阵,随机小数填充
rand(m,n,p):生成m X n X p的矩阵,随机小数填充
a+(b-a)*rand():[b,a]区间小数
‘double’和'single':指定数据类型,放在rand的最后一个参数位置

randi是生成的整数,rand是[0,1]的小数。
randi(iMax):生成[0,iMax]的整数
randi(iMax,m):生成m X m的方阵,数值区间[0,iMax]
randi(iMax,m,n):生成m X n的矩阵,数值区间[0,iMax]
randi(iMax,m,n,p,...):后面的全部都是维度m X n X p X ...
randi([iMin,iMax],m,n):生成m X n的矩阵,数值区间[iMin,iMax]

randn(m):m X m
randn(m,n):m X n
randn(m,n,p):m X n X p
·只有randi能够指定[iMin,iMax],rand、randn都不可以。
·randi生成的是整数,rand、randn生成的是小数。
·randn只能指定维度。
3.元胞数组和结构体
元胞数组:是MATLAB中特有的一种数据类型,是数组的一种,其内部元素可以是属于不同的布局类型,概念理解上,可以认为它和C语言里面的结构体、C++里面的对象很类似。元胞数组是MATLAB中的特色数据类型,它不同于其它数据类型(如字符型,字符数组或者字符串,以及一般的算数数据和数组)。它特有的存取数据方法决定了它的特点,它有给人一种查询信息的感觉,可以逐渐追踪一直到所有的变量全部翻译成基本数据信息。它的class函数输出就是cell(细胞)
元胞数组
A = cell(1,6) %定义
A{2} = eye(3) %2021版本前的matlab下标从1开始
A{5} = magic(5) %魔方:该矩阵无论横、竖还是斜三个方向上的数的和总是相同的
B = A{5}
结构体
注意定义里面是逗号隔开,访问时候用点。
>> books=struct('name',{{'Machine Learning','Data Mining'}},'price',[30,40]) books = 包含以下字段的 struct: name: {'Machine Learning' 'Data Mining'} price: [30 40] >> books.name ans = 1×2 cell 数组 'Machine Learning' 'Data Mining' >> books.price ans = 30 40 >> books.name(1) ans = cell 'Machine Learning' >> books.name{1} ans = Machine Learning
4.矩阵操作
4.1 矩阵的定义与构造
>> A=[1,2,3,4,5,6,7,8,9]%直接定义矩阵
A =
1 2 3 4 5 6 7 8 9
>> B=1:2:9 %第二个参数为步长,不可缺省,[1,9]包含最后一个数值
B =
1 3 5 7 9
>> C = repmat(B,3,2) %重复执行3行2列
C =
1 3 5 7 9 1 3 5 7 9
1 3 5 7 9 1 3 5 7 9
1 3 5 7 9 1 3 5 7 9
>> D = ones(2,4) %生成一个2行4列的全1矩阵
D =
1 1 1 1
1 1 1 14.2 矩阵的四则运算
>> A = [1 2 3 4; 5 6 7 8]
A =
1 2 3 4
5 6 7 8
>> B = [1 1 2 2; 2 2 1 1]
B =
1 1 2 2
2 2 1 1
>> C=A+B %对应位置相加
C =
2 3 5 6
7 8 8 9
>> C=A*B' %'是转置符号
C =
17 13
41 37
>> C=A'*B
C =
11 11 7 7
14 14 10 10
17 17 13 13
20 20 16 16
>> A
A =
1 2 3 4
5 6 7 8
>> B
B =
1 1 2 2
2 2 1 1
>> A.*B %对应位置相乘
ans =
1 2 6 8
10 12 7 8
>> A./B %对应位置相除
ans =
1.0000 2.0000 1.5000 2.0000
2.5000 3.0000 7.0000 8.0000
>> G = A / B %相当于A*B的逆 G*B = A G*B*pinv(B) = A*pinv(B) G = A*pinv(B),相当于A乘B
G =
1.8333 -0.1667
3.1667 1.1667
>> A * inv(B)
错误使用 inv
矩阵必须为方阵。
>> A * pinv(B) %pinv可以不是方阵
ans =
1.8333 -0.1667
3.1667 1.16674.3 矩阵的下标
>> A=magic(5)
A =
17 24 1 8 15
23 5 7 14 16
4 6 13 20 22
10 12 19 21 3
11 18 25 2 9
>> A(2,3) %矩阵坐标从1开始数,访问第二行第二列元素
ans =
7
>> A(2,:) %访问第二行所有元素
ans =
23 5 7 14 16
>> A(:,3) %访问第三列所有元素
ans =
1
7
13
19
25
>> find(A>20) %返回的是大于20的元素的下标,竖着数
ans =
2
6
15
19
23
>> A(6)
ans =
245.程序结构
5.1 for循环结构

>> sum=0;
>> for i=1:5
sum=sum+i*i;
end
>> sum
sum =
55
sum=0;
for i=1:5
cur=1;
for j=1:i
cur=cur*j;
end
sum=sum+cur;
end
disp(sum); %153 
%打印九九乘法表
for i=1:9
for j=1:i
a(i,j)=i.*j;
end
end
disp(a);
>> test01
1 0 0 0 0 0 0 0 0
2 4 0 0 0 0 0 0 0
3 6 9 0 0 0 0 0 0
4 8 12 16 0 0 0 0 0
5 10 15 20 25 0 0 0 0
6 12 18 24 30 36 0 0 0
7 14 21 28 35 42 49 0 0
8 16 24 32 40 48 56 64 0
9 18 27 36 45 54 63 72 815.2 分支结构



7.基本绘图操作
7.1.二维平面绘图
x=0:0.01:2*pi;
y=sin(x);
figure; %建立一个幕布
plot(x,y);
title('y=sin(x)');
xlabel('x');
ylabel('y');
xlim([0 2*pi]); %设置x坐标值的范围

x=0:0.01:20;
y1=200*exp(-0.05*x).*sin(x);
y2=0.8*exp(-0.5*x).*sin(10*x);
figure;
[AX,H1,H2]=plotyy(x,y1,x,y2,'plot');%共用一个x的坐标系,在y上有两个不同的取值
%设置相应的标签
set(get(AX(1),'Ylabel'),'String','Slow Decay');
set(get(AX(2),'Ylabel'),'String','Fast Decay');
xlabel('Time(\musec)');
title('Multiple Decay Rates');
set(H1,'LineStyle','--','Color','b');
set(H2,'LineStyle',':','Color','k');

6.2 三维立体绘图
t=0:pi/50:10*pi;
plot3(sin(t),cos(t),t);
xlabel('sin(t)');
ylabel('cos(t)');
zlabel('t');
%hold on
%hold off %不保留当前操作
grid on;%把图片绘制出来,加一些网格线
axis square %使整个图(连同坐标系)呈方块
hold on是当前轴及图像保持而不被刷新,准备接受此后将绘制的图形,多图共存,即启动图形保持功能,当前坐标轴和图形都将保持,从此绘制的图形都将添加在这个图形的基础上,并自动调整坐标轴的范围。
hold off使当前轴及图像不再具备被刷新的性质,新图出现时,取消原图。即关闭图形保持功能。
hold on 和hold off,是相对使用的。
7.图形的保存与导出
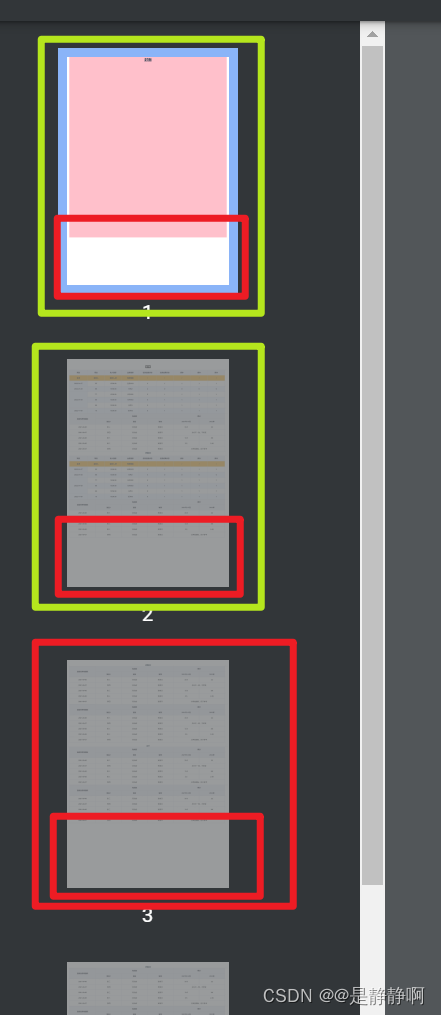
如果直接用截图的方式截取matlab生成的图像,会影响图像的清晰度。因此我们建议:可以用如下方法保存与导出图形。
1)如图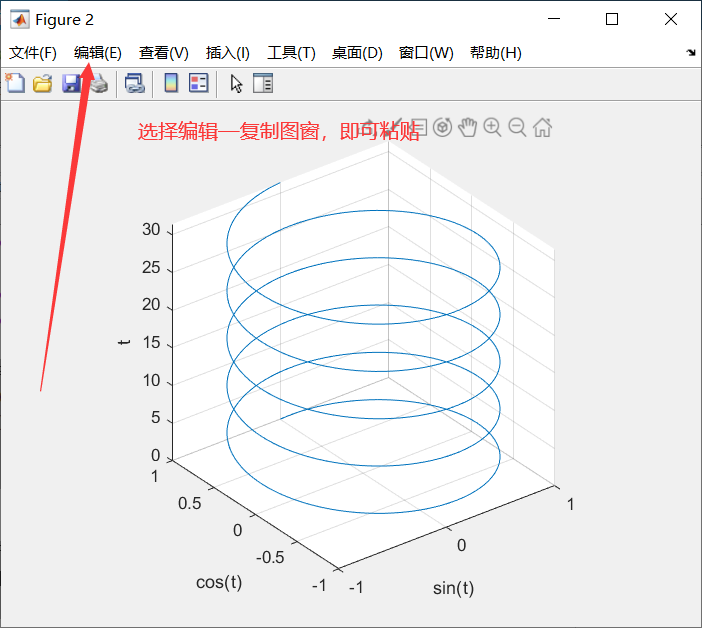

2)编辑→复制选项
可调节相应元素
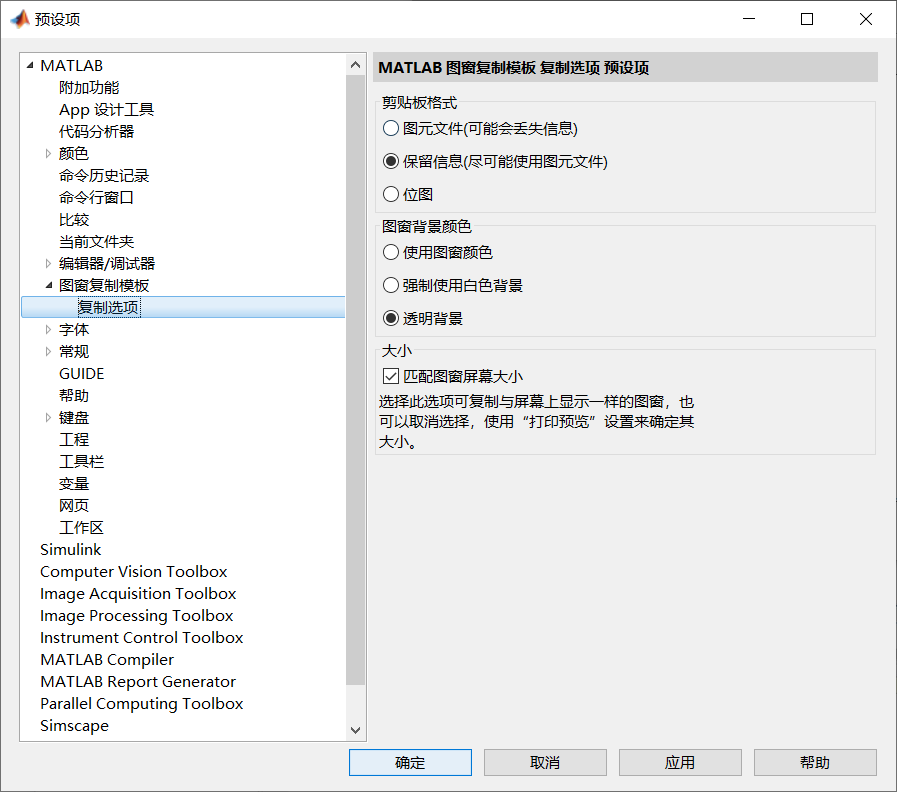
3)编辑→图窗属性
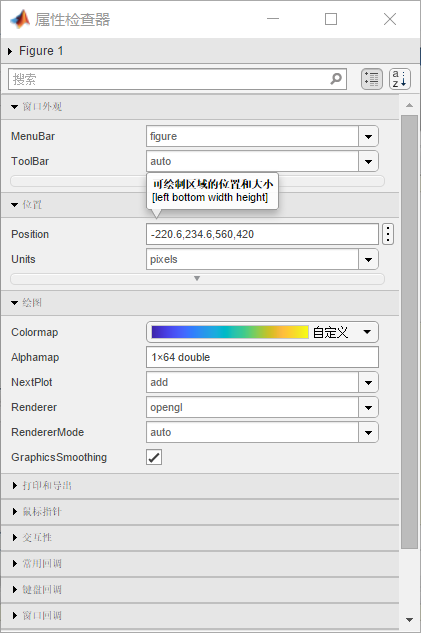
4)文件→导出设置
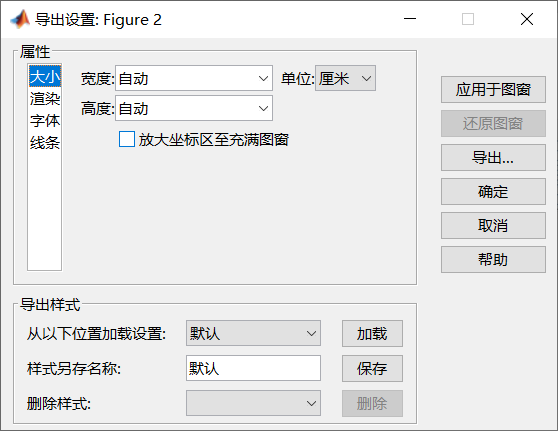
通过调节宽度、高度等像素值属性,可以让图片即使很小,文字依然清晰。
Matlab基础的部分到这就结束了,下面作一点补充~
8.补充
[x,y,z] = peaks(30); %peaks命令用于产生双峰函数或者是用双峰函数绘图
mesh(x,y,z)
grid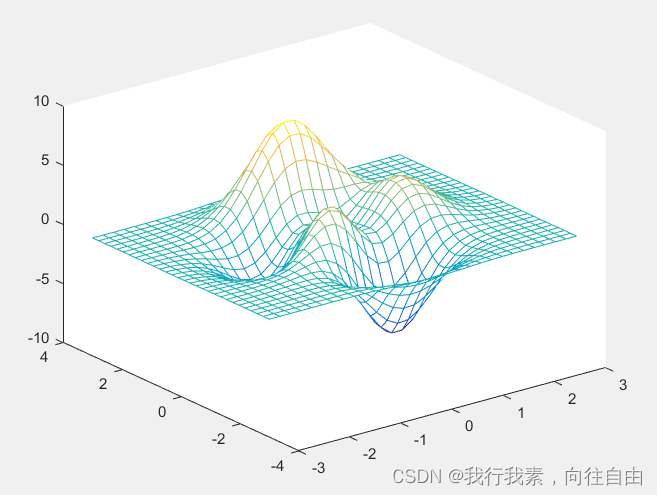
>> peaks
z = 3*(1-x).^2.*exp(-(x.^2) - (y+1).^2) ...
- 10*(x/5 - x.^3 - y.^5).*exp(-x.^2-y.^2) ...
- 1/3*exp(-(x+1).^2 - y.^2)