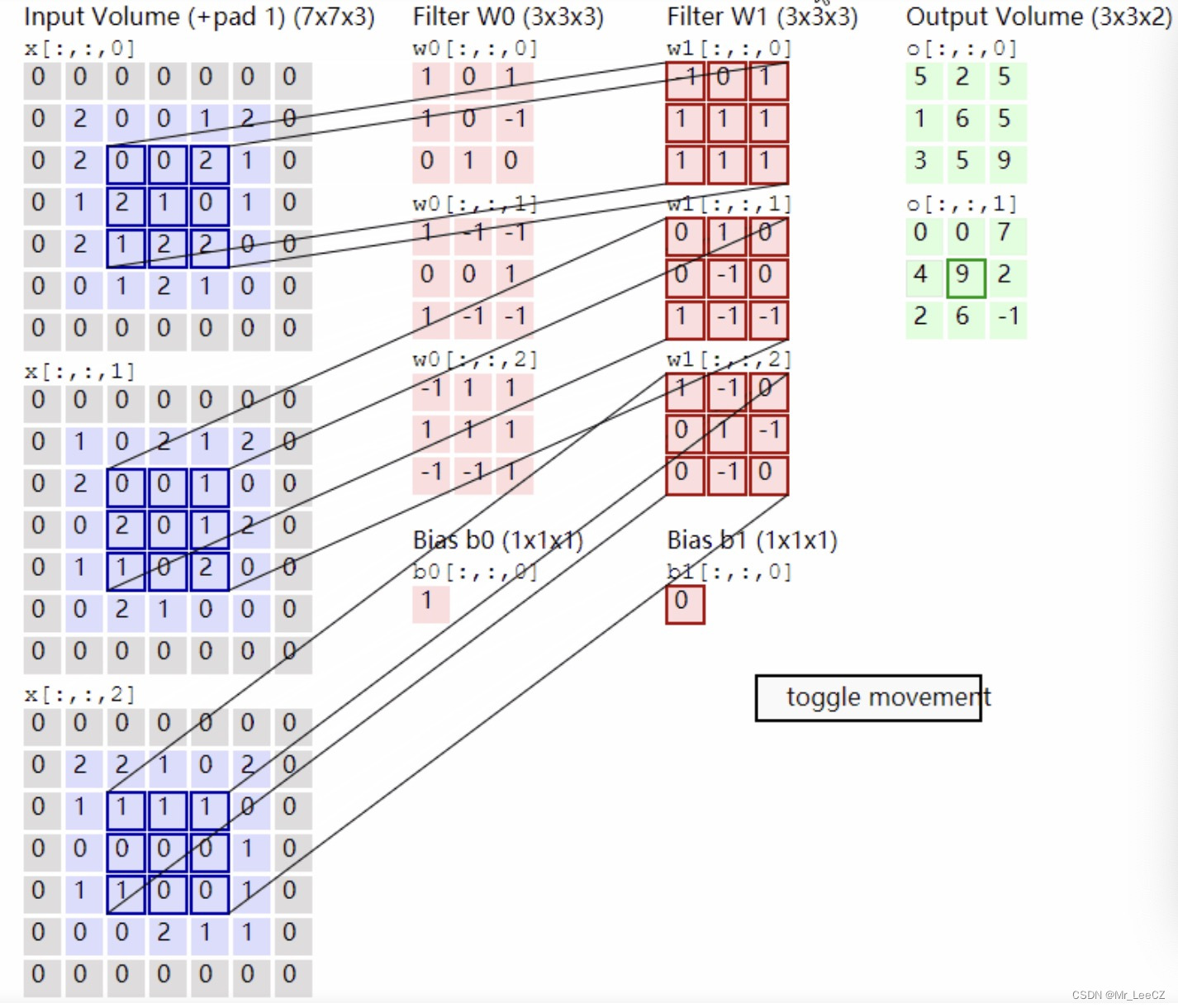
stack 和 queue介绍
两者分别是C++当中的 栈和队列,只不过在C++当中,这两者没有用传统的方式,比如顺序存储和链式存储来实现了,两者现在使用的是一种权限的方式来实现;
都是用容器适配器来实现,开发者考虑到,没有必要在像传统写法一样去实现,直接复用容器来实现即可,如下图官方文档所示,两者都是基于 deque 这个容器来实现的:


而适配器的本质其实就是复用。
两者实现的功能其实和我们在数据结构当中学习的没有什么区别,结构也是一样的;


两者都是容器适配器,不支持我们随便的去遍历,都是有自己的插入删除的规则的,所以这两个容器不支持迭代器。
stack官方文档:stack - C++ Reference (cplusplus.com)
queue官方文档:queue - C++ Reference (cplusplus.com)
stack 和 queue 的 例题
因为 STL 当中的类使用起来都是类似的,而两者的使用非常的简单,所以直接用几个例题来了解 stack 和 queue两个类的使用。
155. 最小栈 - 力扣(LeetCode)
设计一个支持 push ,pop ,top 操作,并能在常数时间内检索到最小元素的栈。
实现 MinStack 类:
MinStack()初始化堆栈对象。void push(int val)将元素val推入堆栈。void pop()删除堆栈顶部的元素。int top()获取堆栈顶部的元素。int getMin()获取堆栈中的最小元素。
问题就在于, geiMin()这个函数,而且要求在 O(1)的时间复杂度。所以不能用常规方式来解决,而且栈也是不支持遍历的。
首先我们想到的是,在MinStack类当中有一个栈容器,有一个Min成员,用于存储栈容器当中的最小值,当push一个比Min小的值就更新Min。这样做有一个很多的问题,当需要Pop的时候,很难及时更新Min。
所以上述方式不可行。
解决这个问题,我们使用两个栈来以空间换时间。一个栈是存储push进去的元素的,也就是存储数据的栈;另一个栈是存储第一个栈的最小值的,只不过存储方式有些许不同:
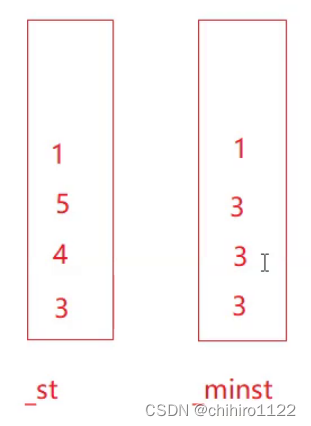
如上图所示,_st 栈就是存储数据的栈,上述的例子push的顺序是 (3 4 5 1)。当_st 入栈 3 时候,此时 3 就是 _st 栈的最小值,那么在 _minst 当中就 push 3;然后 _st 当中 push 4 的时候,此时 _st栈 的最小值还是3,那么 _minst 栈还是 push 3,;接下里的5 也是一样的;当 _st 入栈 1的时候,1变成了 _st 栈的最小值,那么 _minst 栈就push 1。
用上面这样方式来记录没有push进去 _st 栈当中的时候,此时_st栈 当中的最小值是多少。
上述代码还可以进行优化,上述的_minst栈当中存储了多个3,其实这些重复的值是不用删的,只需要入栈更小的元素即可。如下图所示:

注意:上述优化的版本,如果 _st 当中入栈的元素和 _minst 栈顶元素相等的话,也是要入栈的。
可以不写构造函数,写上空的构造函数也是可以的,因为如果这个构造函数实现之后,就算其中没有任何操作,编译器也会去调用初始化列表,而初始化列表默认是,对内置类型不处理,对于自定义类型会去调用这个自定义类型的构造函数。所以,这个构造函数不写,可以;写上一个没有任何操作的空的构造函数也是可以的。
同样析构函数也是没有必要的写的,这里编译器会自动生成,来对 minstack这个类进行处理,而其中的两个栈成员,stack有自己的析构函数来处理,所以在这个类当中,析构函数是不用写的。
代码实现:
class MinStack {
public:
// 可写可不写
MinStack() {
}
void push(int val) {
_st.push(val);
if(_minst.empty() || _minst.top() >= val)
{
_minst.push(val);
}
}
void pop() {
if(_minst.top() == _st.top())
{
_minst.pop();
}
_st.pop();
}
int top() {
return _st.top();
}
int getMin() {
return _minst.top();
}
private:
stack<int> _st;
stack<int> _minst;
};栈的压入、弹出序列_牛客题霸_牛客网 (nowcoder.com)
输入两个整数序列,第一个序列表示栈的压入顺序,请判断第二个序列是否可能为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如序列1,2,3,4,5是某栈的压入顺序,序列4,5,3,2,1是该压栈序列对应的一个弹出序列,但4,3,5,1,2就不可能是该压栈序列的弹出序列。
1. 0<=pushV.length == popV.length <=1000
2. -1000<=pushV[i]<=1000
3. pushV 的所有数字均不相同
判断压入和弹出顺序是否相同,可以进行模拟实现。如下例子分析:
首先这哥例子是满足条件的,那么先从出栈顺序第一个开始判断,逐渐入栈。1 和 3 不相等,那么接着进行入栈,2 和 3 不相等,继续入栈, 3 和 3 相等,入栈3 之后出栈,然后 判断出栈顺序的 2 ,2 和 2 相等,继续出栈;接着,判断出栈顺序的5, 5 和 4 不相等,继续入栈;入栈顺序当中的5 入栈之后 和 出栈顺序当中5 相等,就出栈;接着 4 和 4 相等就出栈,最后入栈和出栈都完毕了。
如果是不满足条件的例子,按照上述的过程,当入栈完毕之后,出栈肯定没完毕,这时候说明不满足条件。
代码实现:
class Solution {
public:
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param pushV int整型vector
* @param popV int整型vector
* @return bool布尔型
*/
bool IsPopOrder(vector<int>& pushV, vector<int>& popV) {
stack<int> st;
int pushi = 0, popi = 0;
while(pushi < pushV.size())
{
st.push(pushV[pushi++]);
if(st.top() != popV[popi])
{
continue;
}
else
{
while(!st.empty() && st.top() == popV[popi])
{
st.pop();
++popi;
}
}
}
return st.empty();
}
};150. 逆波兰表达式求值 - 力扣(LeetCode)
给你一个字符串数组 tokens ,表示一个根据 逆波兰表示法 表示的算术表达式。
请你计算该表达式。返回一个表示表达式值的整数。
我们平常使用的表达式都是中缀表达式,如: 1 + 2 * 3 这样的表达式,中缀表达式就是 操作符在操作数的中间,但是这样不利于计算机识别优先级,计算机识别都是使用的后缀表达式,也就是上面所说的 逆波兰表达式。
他是 操作数的顺序不变,操作符的顺序按照优先级来排列,操作数在前,操作符在后,如:2 + 1 * 3 ,写成后缀表达式就是 2 1 3 * +
上述题目要求只是把给定的后缀表达式 计算出结果,没有要求中缀转后缀,那么只是计算后缀表达式的结果就很简单了。
可以用一个栈来存储结果。首先让所有的操作数入栈,然后再取栈顶的两个元素进行运算,结果入栈。这样就可以计算出后缀表达式的结果。
代码实现:
class Solution {
public:
int evalRPN(vector<string>& tokens) {
stack<int> st;
for(auto& ch : tokens)
{
if(ch == "+" || ch == "-" || ch == "*" || ch == "/")
{
int right = st.top();
st.pop();
int left = st.top();
st.pop();
switch(ch[0])
{
case '+':
st.push(left + right);
break;
case '-':
st.push(left - right);
break;
case '*':
st.push(left * right);
break;
case '/':
st.push(left / right);
break;
}
}
else
{
st.push(stoi(ch));
}
}
return st.top();
}
};对于中缀转后缀,这里是简单的进行思路的解释:还是要用一个栈,一次遍历表达式,如果遇到操作数就直接输出,如果遇到操作符就入栈。
对于操作符入栈操作,有两大情况:
- 栈为空 或者 当前操作符比栈顶 优先级高,继续入栈。
- 栈不为空 或者 当前操作符比栈顶的优先级低或者相等,则输出栈顶操作符
那么这里就涉及到 运算符优先级的问题,这个问题如果用 map建立对应的映射关系可以解决。如果不用map,可以用 if else 或 switch来暴力实现。
102. 二叉树的层序遍历 - 力扣(LeetCode)
给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。
这个题目和普通的层序遍历不一样,他还需要把树每一层结点值都赋值在一个二维数组每一层当中,所以,我们不光要打印,还要判断出当前打印的结点是那一层的。
法一:可以用两个队列,一个队列用于层序遍历,入队和出队树结点;另一个对了存储当前入队的结点属于那一层的层数。如下图所示;
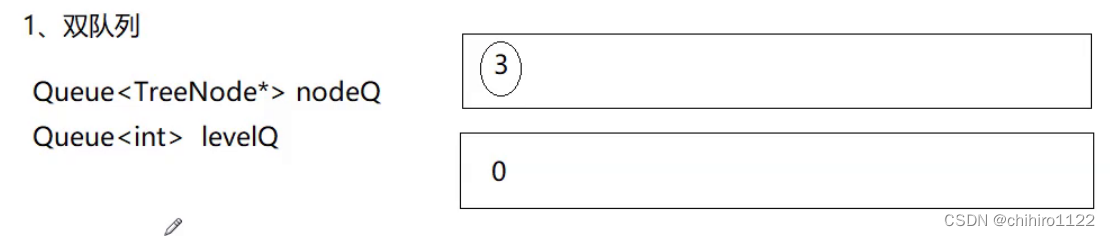
上述的双队列虽然能实现,但是不是最优解。
更优的是使用 一个 levelsize 变量来控制输出每一层的结点:
具体做法是当我 如某一层第一个结点之前,先把这一层的结点个数计算出来,保存到 levelsize当中;然后当我们输出一个这一层的结点的一个结点,levelsize-- ,直到levelsize 减到 0,此时说明这一层的结点已经输出完了。图下图所示(为第三层的输出之前):

我们可以用这样的方式来控制每一层的输出,但是问题在于我们如何计算每一层当中个数呢?
其实,在入队和出队这样循环,直到树当中遍历完全,是一个循环走到底;那么其实在这一层循环当中可以再套一层循环,这一层循环用于输出这一层的结点,当内层循环走完的时候,就是当前层数的结点已经出队完毕,但是这一层的所有孩子已经全部入队,而且此时队列当中的结点全部是上一层父亲结点的给出的孩子结点,也就是说,此时队列当中存储所有结点就是下一层的所有结点。
因此,我们可以直接求出当前队列当中元素个数,赋值给levesize就行了。
代码实现:
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> vv;
queue<TreeNode*> q;
int levelsize = 0;
if(root)
{
q.push(root);
levelsize = 1;
}
while(!q.empty())
{
vector<int> v;
for(int i = 0; i < levelsize;i++)
{
TreeNode* front = q.front();
q.pop();
v.push_back(front->val);
if(front->left)
{
q.push(front->left);
}
if(front->right)
{
q.push(front->right);
}
}
vv.push_back(v);
levelsize = q.size();
}
return vv;
}
};102. 二叉树的层序遍历 - 力扣(LeetCode)
给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。
使用上述方法,然后把用于存储 vv vector 类 reserve一下就行了。