DAY52：动态规划（十七）子序列问题：最长递增子序列+最长连续递增序列+最长重复子数组

news2024/11/27 11:03:50

文章目录

    • 300.最长递增子序列（注意初始化和结果取值）
      • 思路
      • DP数组含义
      • 递推公式
      • 初始化
      • 最开始的写法
      • debug测试：解答错误
        • debug测试2：result初始值
      • 修改完整版
      • 总结
    • 674.最长连续递增序列
      • 思路1：滑动窗口
      • 思路2：动态规划
      • DP数组含义
      • 递推公式
      • 初始化
      • 完整版
    • 718.最长重复子数组
      • 思路1:DP数组定义为下标i和下标j
        • DP数组含义
        • 递推公式
        • 初始化
        • 遍历顺序
        • 最开始的写法
        • debug测试：解答错误
        • 思路1完整版
        • 总结
      • 思路2:（推荐）DP数组定义为i对应nums[i-1]
        • DP数组含义
        • 递推公式
        • 初始化
        • 思路2完整版
        • 总结

  • 子序列系列是DP重要系列，关键就是掌握状态的递推，dp[i]可以从哪些状态推出来！

300.最长递增子序列（注意初始化和结果取值）

给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。

子序列 是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。

示例 1：

输入：nums = [10,9,2,5,3,7,101,18]
输出：4
解释：最长递增子序列是 [2,3,7,101]，因此长度为 4 。

示例 2：

输入：nums = [0,1,0,3,2,3]
输出：4

示例 3：

输入：nums = [7,7,7,7,7,7,7]
输出：1

提示：

  • 1 <= nums.length <= 2500
  • -10^4 <= nums[i] <= 10^4

思路

本题属于子序列类的题目，首先要明确什么是子序列。

子序列 是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。也就是说元素并不需要连续。

DP数组含义

本题正确定义DP数组含义非常重要。

dp[i]的含义是，包含下标i在内，也就是包含nums[i]数字在内的递增子序列的长度。

递推公式

本题的递推核心在于找下标i范围以内的，能够满足递增条件的数字，增加到下标i的长度里面。

例如，从最开始的dp[1]开始分析，因为递增序列最小长度为1所以初始值为1。

if(nums[1]>nums[0])  dp[1]=dp[0]+1

再分析dp[2]，对于下标2，应分析所有下标2以内的数字，能不能与nums[2]构成递增。

if(nums[2]>nums[0]) dp[2]=dp[0]+1;
if(nums[2]>nums[1]) dp[2]=dp[1]+1;

由上面的推导逻辑可知，每遍历一个i内部的j，dp[i]都会进行长度的更新，我们最后的dp[i]需要选长度最大的！

因此得到最后的递推公式：

dp[i]=max(dp[i],dp[j]+1);

完整的递推逻辑如下：

//注意i和j的取值，是从初始状态推过来的
for(int i=1;i<nums.size();i++){
    for(int j=0;j<i;j++){
        //如果满足递增，那么更新dp[i]
        if(nums[i]>nums[j]){
            dp[i]=max(dp[i],dp[j]+1)
        }    
    }
}

初始化

dp[0]=1，因为递增序列的最短长度就是1（参考用例）。

但是本题需要特别注意，需要所有的dp[i]都初始化为1，而不是0！因为dp[i]指的是每个以下标i为结束的递增子序列的长度，该长度最少是1！

举个例子，当dp[2]=dp[1]+1的时候，如果在这之前nums[1]<nums[0]，dp[1]没有得到累加，那么dp[1]此刻的数值应该是1！才能让dp[2]是正确的最大长度！

最开始的写法

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        vector<int>dp(nums.size(),0);
        //初始化，dp[0]是一切递推的基础
        dp[0]=1;
        for(int i=1;i<nums.size();i++){
            for(int j=0;j<i;j++){
                //如果i的末尾元素大于j的末尾元素，那么就在j长度基础上+1，最后取最大的dp[i]
                if(nums[i]>nums[j])
                	dp[i]=max(dp[i],dp[j]+1);
            }
        }
        return dp[nums.size()-1];
    }
};

debug测试：解答错误

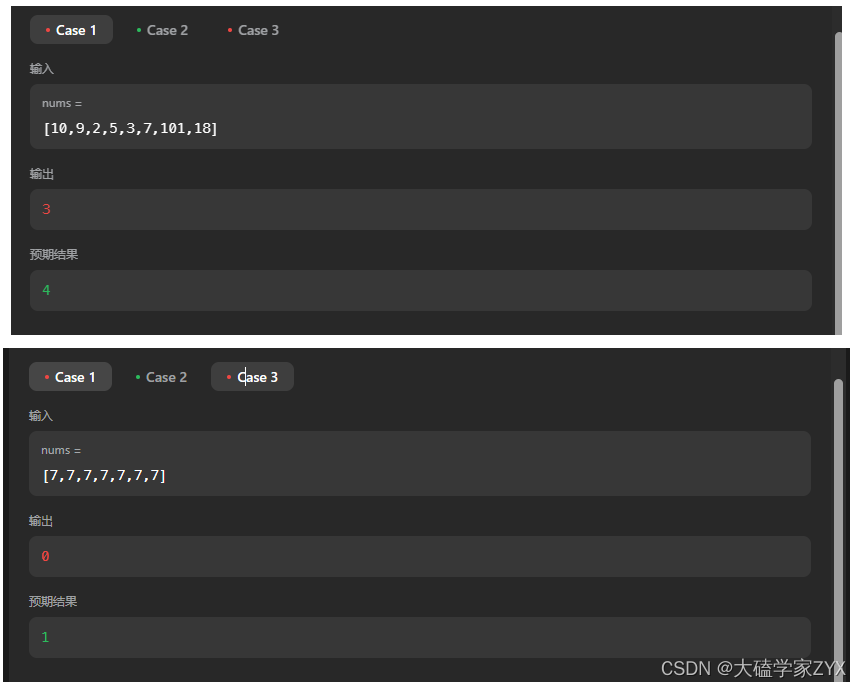
在这里插入图片描述
由最后一个case我们可以看出问题，就是dp[i]的数值，没有保持到最后。

因此，我们应该在dp数组中，取所有dp[i]的最大值，因为这里的dp[i]是针对每个以下标i结束的子序列，所以最后的最大值不一定在dp数组末尾！

并且最开始写法的初始化也有问题，以i为结尾的递增子序列，其长度最少为1！

debug测试2：result初始值

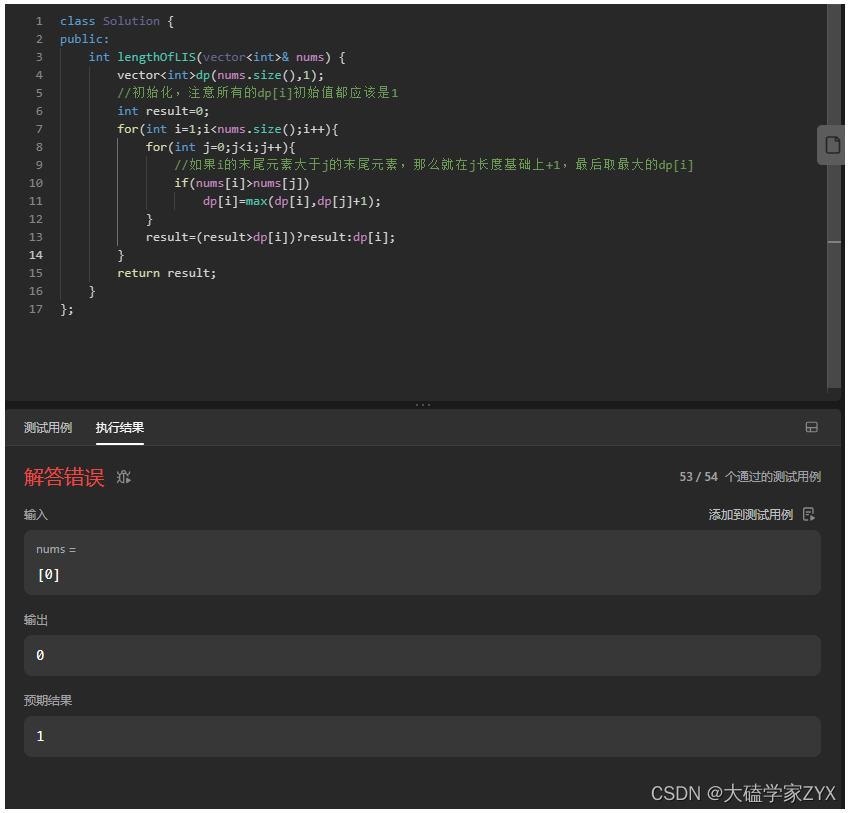
在这里插入图片描述
另外还需要注意，因为i从1开始所以res并没有和dp[0]比较，因此res初始值也应该是1（防止只有一个元素的时候，根本不比较直接输出）

修改完整版

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        vector<int>dp(nums.size(),1);
        //初始化，注意所有的dp[i]初始值都应该是1
        int result=1;
        for(int i=1;i<nums.size();i++){
            for(int j=0;j<i;j++){
                //如果i的末尾元素大于j的末尾元素，那么就在j长度基础上+1，最后取最大的dp[i]
                if(nums[i]>nums[j])
                	dp[i]=max(dp[i],dp[j]+1);//dp[i]存放dp[i]的最大值
            }
            result=(result>dp[i])?result:dp[i];
        }
        return result;
    }
};
  • 时间复杂度: O(n^2)
  • 空间复杂度: O(n)

总结

  • 本题的最大值并不在dp数组末尾，因为每个数据都可能比前面的数字要小。最大长度可能是dp数组中间位置的dp[i]，所以需要建个result存最大值。
  • 初始化要注意，本题每个以i为结尾的递增子序列，长度最小是1而不是0！

674.最长连续递增序列

给定一个未经排序的整数数组，找到最长且 连续递增的子序列，并返回该序列的长度。

连续递增的子序列 可以由两个下标 l 和 r（l < r）确定，如果对于每个 l <= i < r，都有 nums[i] < nums[i + 1] ，那么子序列 [nums[l], nums[l + 1], ..., nums[r - 1], nums[r]] 就是连续递增子序列。

示例 1：

输入：nums = [1,3,5,4,7]
输出：3
解释：最长连续递增序列是 [1,3,5], 长度为3。
尽管 [1,3,5,7] 也是升序的子序列, 但它不是连续的，因为 5 和 7 在原数组里被 4 隔开。

示例 2：

输入：nums = [2,2,2,2,2]
输出：1
解释：最长连续递增序列是 [2], 长度为1。

提示：

  • 1 <= nums.length <= 10^4
  • -10^9 <= nums[i] <= 10^9

思路1：滑动窗口

本题是求连续递增子序列的长度，此时第一反应是滑动窗口。

滑动窗口的算法专题里面整理过类似的题目：算法专题整理：滑动窗口_大磕学家ZYX的博客-CSDN博客

在这里插入图片描述

上面这道题目求的也是连续的最长子序列的长度，这两道题的做法类似但是有一定的区别。

本题的滑动窗口做法：

  • 遇到不是递增的，直接更新左端点
class Solution {
public:
    int findLengthOfLCIS(vector<int>& nums) {
        if(nums.size()==1) return 1;
        //开始滑动
        int res=1;
        int start=0;//先从下标0位置开始找
        for(int i=1;i<nums.size();i++){
            //只要不是递增，直接修改左端点
            if(nums[i]<=nums[i-1]){
                start=i;
            }
            res=max(res,i-start+1);//res存放长度的最大值
        }
        return res;

    }
};

2779.数组最大美丽值的滑动窗口做法：

  • 排序之后找左右窗口端点值相减<=2k的窗口，并求窗口最大长度
class Solution {
public:
    int maximumBeauty(vector<int>& nums, int k) {
        sort(nums.begin(), nums.end());
        int res=1;//这道题子序列是找相等元素
        for(int left=0,right=0;right<nums.size();right++){
            //因为是找最大长度，所以是不符合<=条件了，才移动左端点
            while((nums[right]-nums[left])>2*k){
                left++;
            }
            res=max(res,right-left+1);//res存放长度的最大值
        }
        return res;
    }
};

从这两个题目对比也可以看出来，滑动窗口指的是遍历右端点，按照条件移动左端点。

在最长连续递增子序列的问题中，需要找的是数组中最长的递增子序列。所以当发现当前元素不大于前一个元素时，窗口的左端点直接跳到新的位置求新的递增长度，不需要慢慢滑动。

在数组最大美丽值中，需要找的是数组中最长的由相等元素组成的子序列，且可以将数组中的元素替换为它加减k的结果。因此当发现窗口right-k大于窗口left+k时，需要将窗口的左边界进行滑动。

这两道题目的滑动窗口思想是类似的，都是通过移动窗口的左右边界来找到最长的满足某种条件的子序列。

思路2：动态规划

但是其实没必要用滑动窗口，因为本题求递增子序列，左端点不用滑，只要一直枚举右端点能不能扩，断开的话将左端点移到右端点的位置即可。

本题可以像上一题最长递增子序列一样用DP解决。

DP数组含义

dp[i]指的是包括下标i的nums[i]在内的递增子序列的最大长度。

递推公式

  • 本题是求连续的子序列，因此只需要一层循环即可，不需要两层循环找不连续的递增！
for(int i=0;i<nums.size();i++){
    if(nums[i]>nums[i-1]){
        dp[i]=dp[i-1]+1;//这么做相当于断开的时候重新计数！
    }
}

初始化

和上一题一样，每个数字自身就是一个子序列，因此所有dp[i]都应该初始化为1！

完整版

class Solution {
public:
    int findLengthOfLCIS(vector<int>& nums) {
        vector<int>dp(nums.size(),1);
        if(nums.size()==1) return 1;
        //记录长度的初始值
        int res=1;
        for(int i=1;i<nums.size();i++){
            if(nums[i]>nums[i-1]){
                dp[i]=dp[i-1]+1;
            }
            res=max(res,dp[i]);//res存放dp[i]的最大值
        }
        return res;
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(1)

718.最长重复子数组

给两个整数数组 nums1 和 nums2 ，返回 两个数组中 公共的 、长度最长的子数组的长度 。

示例 1：

输入：nums1 = [1,2,3,2,1], nums2 = [3,2,1,4,7]
输出：3
解释：长度最长的公共子数组是 [3,2,1] 。

示例 2：

输入：nums1 = [0,0,0,0,0], nums2 = [0,0,0,0,0]
输出：5

提示：

  • 1 <= nums1.length, nums2.length <= 1000
  • 0 <= nums1[i], nums2[i] <= 100

思路1:DP数组定义为下标i和下标j

本题难点在于，比较两个数组，得到重复且连续的最长子数组，用一维的DP数组无法同时表示两个数组的状态。

我们需要用一个二维的矩阵来比较两个数组的所有状态。

DP数组含义

第一种思路，我们直接让i对应下标i，j对应下标j。

dp[i][j]表示第一个数组在下标i位置，第二个数组在下标j位置，此时最长重复子数组的长度是dp[i][j]

递推公式

  • 核心点是连续，所以从dp[i-1][j-1]的状态转移过来
for(int i=1;i<nums.size();i++){
    for(int j=1;j<nums.size();j++){
        if(nums1[i]==nums2[j]){
            //从i-1,j-1转移过来，因为是重复连续子序列，所以i-1和j-1必须也要重复且连续
            dp[i][j]=dp[i-1][j-1]+1;
        }
    }
}

初始化

初始化包括dp[i][0]和dp[0][j]的情况。

dp[i][0]的含义是，两个数组下标分别为i和0的情况下，重复子序列的长度。因此需要把num1的数字和nums2下标为0的数字进行一一比对，如果相等就需要+1！

dp[0][j]同理。

//定义DP数组，i对应nums1，j对应nums2
vector<int>(nums1.size(),vector<int>(nums2.size(),0));

for(int i=0;i<nums1.size();i++){
    if(nums1[i]==nums2[0])  dp[i][0]=1;
}
for(int j=0;j<nums2.size();j++){
    if(nums2[j]==nums1[0]) dp[0][j]=1;
}

遍历顺序

遍历顺序任意一个for循环在外都可以

最开始的写法

class Solution {
public:
    int findLength(vector<int>& nums1, vector<int>& nums2) {
        vector<vector<int>>dp(nums1.size(),vector<int>(nums2.size(),0));
        //初始化
        for(int i=0;i<nums1.size();i++){
            if(nums1[i]==nums2[0])  dp[i][0]=1;
        }
        for(int j=0;j<nums2.size();j++){
            if(nums2[j]==nums1[0])  dp[0][j]=1;
        }
        //开始遍历
        int result=0;
        for(int i=1;i<nums1.size();i++){
            for(int j=1;j<nums2.size();j++){
                if(nums1[i]==nums2[j])
                    dp[i][j]=dp[i-1][j-1]+1;
                    //存dp[i][j]中的最大值
                	result=max(result,dp[i][j]);
            } 
        }
        //遍历找二维数组整个数组中的最大值，因为最大值不一定在末尾！
        return result;
    }
};

debug测试：解答错误

在这里插入图片描述
会出现这种解答错误的原因，是因为本题需要用result记录整个二维DP数组中，DP值最大的数值！

而像图中这样写，i=0,j=0状态下相等的数值，就没有记录进result里面（初始化的时候result没有计数）

在这里插入图片描述
因此，下面的for循环也应该从i=0,j=0开始写！为的就是方便result统计所有DP数组中的数值，从而找最大值。

思路1完整版

class Solution {
public:
    int findLength(vector<int>& nums1, vector<int>& nums2) {
        vector<vector<int>>dp(nums1.size(),vector<int>(nums2.size(),0));
        //初始化
        for(int i=0;i<nums1.size();i++){
            if(nums1[i]==nums2[0])  dp[i][0]=1;
        }
        for(int j=0;j<nums2.size();j++){
            if(nums2[j]==nums1[0])  dp[0][j]=1;
        }
        //开始遍历
        int result=0;
        //注意从i=0,j=0开始遍历的话，一定要在递推公式的地方进行边界检查！
        for(int i=0;i<nums1.size();i++){
            for(int j=0;j<nums2.size();j++){
                if(nums1[i]==nums2[j]&&i>0&&j>0)
                    dp[i][j]=dp[i-1][j-1]+1;
                    //存dp[i][j]中的最大值
                //不管是否有数字相等，都更新result，就是为了增加[0][j]的情况！
                result=max(result,dp[i][j]);
            } 
        }
        //遍历找二维数组整个数组中的最大值，因为最大值不一定在末尾！
        return result;
    }
};

总结

这种思路的注意点：

  • dp[0][j]和dp[i][0]的情况都需要单独初始化
  • 但是单独初始化的情况并没有被result包括，因此为了包括在内，底下遍历的时候必须从0开始！就是为了 result=max(result,dp[i][j]);这句话能够包含[0][j]和[i][0]的情况！

思路2:（推荐）DP数组定义为i对应nums[i-1]

DP数组含义

dp[i][j]：长度为[0, i - 1]的字符串text1与长度为[0, j - 1]的字符串text2的最长重复子序列为dp[i][j]

也就是说dp[i][j]对应的是包含nums1[i-1]和nums2[j-1]在内的最长重复子序列！

递推公式

//这种做法，直接从1开始就行，因为dp[i]对应nums1[i-1]
//i的结束是nums.size()
for(int i=1;i<=nums1.size();i++){
    for(int j=1;j<=nums2.size();j++){
        if(nums1[i]==nums2[j])
        	dp[i][j]=dp[i-1][j-1]+1;
        result=max(result,dp[i][j]);
    }
}

初始化

根据dp[i][j]的定义，dp[i][0] 和dp[0][j]其实都是没有意义的，此时的初始化直接初始化为0即可。

看完整版代码，如果nums1[0]==nums2[0]，那么dp[1][1]=dp[0][0]+1=1

思路2完整版

class Solution {
public:
    int findLength(vector<int>& nums1, vector<int>& nums2) {
        vector<vector<int>>dp(nums1.size()+1,vector<int>(nums2.size()+1,0));
        //初始化不需要管，dp[i][0]和dp[0][j]全部置为0即可，因为没有意义
        int res=0;
        for(int i=1;i<=nums1.size();i++){
            for(int j=1;j<=nums2.size();j++){
                if(nums1[i-1]==nums2[j-1]){
                    dp[i][j]=dp[i-1][j-1]+1;
                }
                //收集所有dp[i][j]中的最大值
                res = max(res,dp[i][j]);
            }
        }
        return res;      
    }
};

总结

  • 思路2的做法简化了初始化，使得i=0和j=0情况不需要单独对比，并且使得for循环可以正常从i=1开始防止下标越界，但仍然遍历所有数字。

由思路1和思路2的对比可以看出，这种两个序列对比的类型题目，最好还是把DP数组定义为：

以下标i - 1为结尾的A，和以下标j - 1为结尾的B，最长重复子数组长度为dp[i][j]。 （特别注意： “以下标i - 1为结尾的A” 标明一定是 以A[i-1]为结尾的字符串 ，而不是考虑了[i-1]结尾的字符串！）

因为本题是找重复，找重复的话所有元素都必须比较，所以和打家劫舍那种"“考虑前i栋房屋”"的类型不一样。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/792520.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【Leetcode】54.螺旋矩阵

【Leetcode】54.螺旋矩阵

一、题目 1、题目描述 给你一个 m m m 行 n n n 列的矩阵 matrix，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。 示例1： 输入：matrix =
阅读更多...
安防监控视频汇聚EasyCVR修改录像计划等待时间较长，是什么原因？

安防监控视频汇聚EasyCVR修改录像计划等待时间较长，是什么原因？

安防监控视频EasyCVR视频融合汇聚平台基于云边端智能协同&#xff0c;支持海量视频的轻量化接入与汇聚、转码与处理、全网智能分发等。音视频流媒体视频平台EasyCVR拓展性强&#xff0c;视频能力丰富&#xff0c;具体可实现视频监控直播、视频轮播、视频录像、云存储、回放与检…
阅读更多...
项目——负载均衡在线OJ

项目——负载均衡在线OJ

目录 项目介绍开发环境所用技术项目宏观结构编写思路1. 编写compile_server1.1 编译模块编写1.2 运行功能1.3compile_runner 编译与运行1.4 编写compile_server.cpp调用compile_run模块&#xff0c;形成网络服务 2. 编写基于MVC的oj_server2.1 oj_server.cpp的编写2.2 oj_model…
阅读更多...
Unity进阶--对象池数据场景管理器笔记

Unity进阶--对象池数据场景管理器笔记

文章目录 泛型单例类泛型单例类&#xff08;不带组件版&#xff09;对象池管理器数据管理器场景管理器 泛型单例类 using System.Collections; using System.Collections.Generic;public abstract class ManagersSingle<T> where T : new() {private static T instance;…
阅读更多...
OSCP 学习：Kali Linux 基本命令

OSCP 学习：Kali Linux 基本命令

Bash 环境 环境变量 当我们开启新的bash时候&#xff0c;它会拥有自己的环境变量 我是这样理解 环境变量的&#xff1a; 每个程序都有自己运行的地址 我们用一个变量来储存它的地址 这个变量就叫环境变量 Kali 最常用的环境变量 就是 $PATH。这个我们可以用这个变量进行不正当…
阅读更多...
selenium浏览器驱动下载

selenium浏览器驱动下载

Chrome谷歌浏览器 下载地址&#xff1a;http://chromedriver.storage.googleapis.com/index.html 不同的Chrome的版本对应的chromedriver.exe 版本也不一样&#xff0c;下载时不要搞错了。 如果是最新的Chrome, 下载最新的chromedriver.exe 就可以了。 Firefox火狐浏览器 驱…
阅读更多...
B073-封装工具类 服务模块(后台)

B073-封装工具类 服务模块(后台)

目录 拿当前登录人信息工具类服务模块业务分析表结构后端代码后台代码覆写删除-加详情一起删调整前端Data&#xff0c;handleAdd和编辑框覆写新增编辑按钮展示详情资源&#xff1a;多图上传和回显图片 拿当前登录人信息工具类 工具类准备&#xff1a;LoginContext: 登录上下文…
阅读更多...
前端性能测试

前端性能测试

目录 前言&#xff1a; 前端性能 1、优化 2、Lighthouse 使用 4、Lighthouse 报告参数的标准 5、更多产品 前言&#xff1a; 前端性能测试是一个广泛的领域&#xff0c;它旨在评估前端应用程序的性能和可靠性。前端性能测试需要使用各种测试工具和技术&#xff0c;包括浏…
阅读更多...
功率信号源的基本工作原理、用途和应用方法

功率信号源的基本工作原理、用途和应用方法

功率信号源是一种可以产生恒定或可变功率输出的测试设备。在电子实验中&#xff0c;功率信号源广泛应用于各种不同的应用&#xff0c;下面安泰电子就来介绍功率信号源的基本工作原理、用途和应用方法。 功率信号源的基本工作原理 功率信号源的基本工作原理是将电能转换成信号能…
阅读更多...
【前端实习评审】对小说详情模块的产品原型有一定的自己理解

【前端实习评审】对小说详情模块的产品原型有一定的自己理解

大家好&#xff0c;本篇文章分享一下【校招VIP】免费商业项目“推推”第一期书籍详情模块前端同学的文档作品。该同学来自中国科学院大学计算机技术专业。 本项目亮点难点&#xff1a;1 热门书籍在更新点的访问压力 2 书籍更新通知的及时性和有效性 3 书荒:同好推荐的可能性 4…
阅读更多...
血压诊断米家智能血压计方案

血压诊断米家智能血压计方案

智能血压计产品介绍: 智能血压计是一种基于蓝牙技术的便携式血压测量设备。它通过无线连接与智能手机或其他设备同步并联接到APP端&#xff08;米家&#xff09;&#xff0c;可以准确测量用户的血压数据&#xff0c;并通过手机应用程序进行记录和分析。 智能血压计产品结构: 智…
阅读更多...
Win10的两个实用技巧系列之蓝屏代码大全及解决方案、更改应用优先级的技巧

Win10的两个实用技巧系列之蓝屏代码大全及解决方案、更改应用优先级的技巧

Win10怎么设置程序优先级? Win10更改应用优先级的技巧 Win10怎么设置程序优先级&#xff1f;Win10系统中任务管理器想要设置优先级&#xff0c;该怎么设置呢&#xff1f;下面我们就来看看Win10更改应用优先级的技巧 有些Win10用户想要调整程序优先级&#xff0c;以确保某些…
阅读更多...
Sentinel限流中间件

Sentinel限流中间件

目录 介绍 Sentinel 的特征 Sentinel 的组成 实战使用 简单实例 配置本地控制台 使用可视化ui配置简单流控 配置异步任务限流 使用注解定义限流资源 SpringCloud整合Sentinel 简单整合 并发线程流控 关联模式 整合openFeign使用 介绍 随着微服务的流行&#xff0…
阅读更多...
iOS私钥证书和证书profile文件的生成攻略

iOS私钥证书和证书profile文件的生成攻略

在使用uniapp打包ios app的时候&#xff0c;要求我们提供一个私钥证书和一个证书profile文件&#xff0c;私钥证书可以使用mac电脑的钥匙串访问程序来生成&#xff0c;也可以使用香蕉云编来生成。证书profile文件可以直接在苹果开发者中心生成。 有部分刚接触ios开发的同学们&…
阅读更多...
Easy-Es笔记

Easy-Es笔记

一、Easy-ES概述 Easy-Es&#xff08;简称EE&#xff09;是一款ElasticSearch-ORM框架&#xff0c;在原生 RestHighLevelClient 的基础上&#xff0c;只做增强不做改变&#xff0c;为简化开发、提高效率而生。Easy-Es采用和MP一致的语法设计&#xff0c;能够显著降低ElasticSea…
阅读更多...
各种拉格朗日函数

各种拉格朗日函数

目录 一&#xff0c;拉格朗日函数 二&#xff0c;部分拉格朗日函数 三&#xff0c;增广拉格朗日函数 一&#xff0c;拉格朗日函数 以三元函数为例&#xff1a; 求f(x,y,z)的极值&#xff0c;s.t.g(x,y,z)0 拉格朗日函数L(x,y,z,a) f(x,y,z) a * g(x,y,z) 在极值点处一…
阅读更多...
（学习日记）2023.06.09

（学习日记）2023.06.09

写在前面&#xff1a; 由于时间的不足与学习的碎片化&#xff0c;写博客变得有些奢侈。 但是对于记录学习&#xff08;忘了以后能快速复习&#xff09;的渴望一天天变得强烈。 既然如此 不如以天为单位&#xff0c;以时间为顺序&#xff0c;仅仅将博客当做一个知识学习的目录&a…
阅读更多...
Spring AOP（面向切面编程）的详细讲解

Spring AOP（面向切面编程）的详细讲解

1.什么是 AOP&#xff1f; AOP&#xff08;Aspect Oriented Programming&#xff09;&#xff1a;⾯向切⾯编程&#xff0c;它是⼀种思想&#xff0c;它是对某⼀类事情的集中处理 AOP是一种思想&#xff0c;而Spring AOP是一个实现了AOP的思想框架&#xff0c;他们的关系和IOC…
阅读更多...
PCIe Error Signaling and Logging持续更新

PCIe Error Signaling and Logging持续更新

来源PCI5.0 SPEC 1.错误报告范式ERROR REPORTING PARADIGMS PCI Express定义了两种错误报告范式&#xff1a;baseline capability and the Advanced Error Reporting Capability。baseline错误报告能力是所有PCI Express设备都需要具备的&#xff0c;它定义了最低限度的错误报…
阅读更多...
基于Ubuntu 22.04 编译chip-tool工具

基于Ubuntu 22.04 编译chip-tool工具

前言 编译过程有点曲折&#xff0c;做下记录&#xff0c;过程中&#xff0c;有参考别人写的博客&#xff0c;也看github 官方介绍&#xff0c;终于跑通了~ 环境说明&#xff1a; 首先需要稳定的梯子&#xff0c;可以访问“外网”ubuntu 环境&#xff0c;最终成功实验在Ubunt…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023