目录
一,拉格朗日函数
二,部分拉格朗日函数
三,增广拉格朗日函数
一,拉格朗日函数
以三元函数为例:
求f(x,y,z)的极值,s.t.g(x,y,z)=0
拉格朗日函数L(x,y,z,a) = f(x,y,z) + a * g(x,y,z)
在极值点处一定有,L对4个变量的一阶偏导为0,从而求出4个变量。
PS:
要求的是拉格朗日函数的驻点,不一定是极值点,也可能是鞍点
二,部分拉格朗日函数
以一阶原始对偶为例:
求:min f(x) + g(Ax),其中f和g 是凸函数。
部分拉格朗日函数:
PS:
要求的是部分拉格朗日函数的鞍点,但是实际上我们不用求导来求,而是迭代寻找鞍点的近似点。
三,增广拉格朗日函数
求:
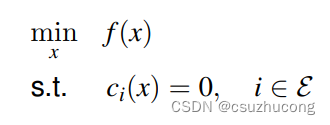
增广拉格朗日函数:
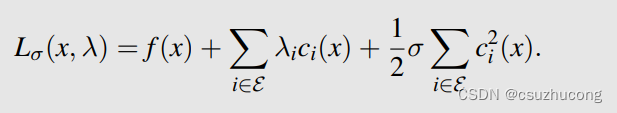
PS:
要求的是 增广拉格朗日函数的最值,它的最值就是原问题的最值的近似值。