4.5 光照模型（Lighting/Illumination Model）

4.5.1 Flat Shading（平面着色）

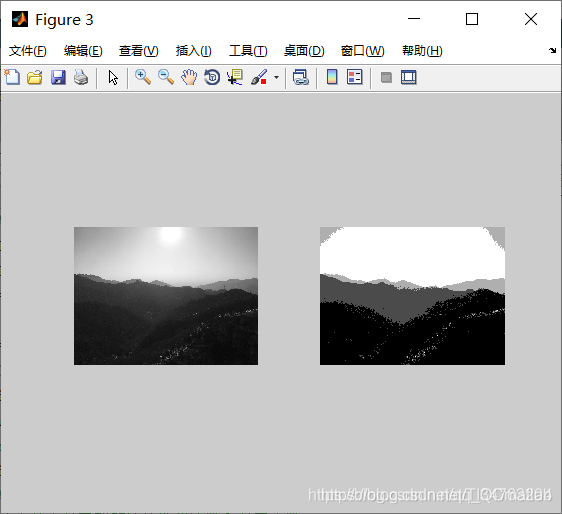
根据表面法向量计算光照，并应用到整个面片上。速度最快，效果最差，容易暴露物体的多边形本质（下图）。

4.5.2 Gouraud Shading（高洛德着色）

根据顶点法向量计算光照，再用插值计算出整个面的光照。效果比Flat shading稍好，但高光部分有瑕疵，过渡不够自然（下图）。

可结合Phong Shading做优化，高光弱时用Gouraud Shading，高光强时用Phong Shading，可平衡效果和效率。

4.5.3 Lambert Shading（兰伯特着色）

物体表面向各个方向等强度的反射光，这种等同地向各个方向散射的现象称为光的漫反射。Lambert定律：反射光线的强度与表面法线和光源方向之间的夹角成正比（下图）。它是一种理想的漫反射模型，但着色效果比高洛德要平滑。

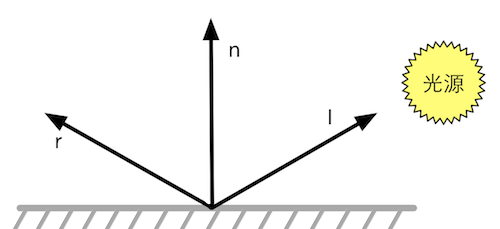
计算公式：

cdiffuse=(clight⋅mdiffuse)max(0,n⃗ ⋅l⃗ )cdiffuse=(clight⋅mdiffuse)max(0,n→⋅l→)

4.5.4 Half Lambert Shading（半兰伯特着色）

Lambert着色有个缺陷，就是背面受光少，经常处理死黑状态，与受光面反差太大（下图左）。于是其中的一种改进方案诞生了，它就是Half Lambert Shading，它渲染的画面明暗关系没那么强烈，过渡更加自然（下图右）。

计算公式：

cdiffuse=(clight⋅mdiffuse)(a(n⃗ ⋅l⃗ +b)cdiffuse=(clight⋅mdiffuse)(a(n→⋅l→+b)

其中aa和bb是常数，通常都取0.50.5，而且a+b=1.0a+b=1.0。

4.5.5 Phong Shading（冯氏着色）

Phong着色将光照分成自发光（Emissive）/环境光（Ambient）/漫反射（Diffuse）/高光（Specular）四个部分，每个部分独自计算光照贡献量。是当前广泛应用的一种光照模型。

其中高光计算公式：

cspecular=(clight⋅mspecular)max(0,n⃗ ⋅r⃗ )mglosscspecular=(clight⋅mspecular)max(0,n→⋅r→)mgloss

Phong着色效果如下：

4.5.6 Blinn-Phong Shading

由于Phong模型要用到反射矢量rr，而rr计算比较耗时（下），故有了Blinn Phong。

r⃗ =2(n⃗ ⋅l⃗ )n⃗ −l⃗ r→=2(n→⋅l→)n→−l→

Blinn Phong是Phong的一个改进，做法是摒弃反射矢量rr，引入l和vv的中间矢量hh，然后利用nn和hh的夹角进行计算。

　　

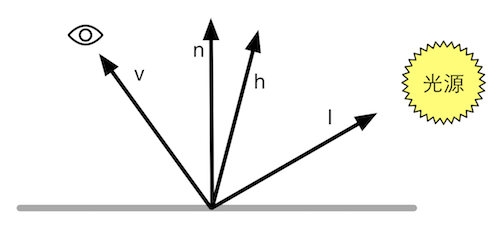
高光计算公式：

cspecular =(clight ⋅mspecular )max(0,n⃗ ⋅h⃗ )mgloss cspecular =(clight ⋅mspecular )max(0,n→⋅h→)mgloss 

它渲染出的高光范围更大（下图），真实感不如Phong着色，但胜在效率更高。

4.5.7 光照模型的选择

从性能上做比较：Flat > Gouraud > Lambert > Half Lambert > Blinn-Phong > Phong。但画质效果刚好相反，所以每个游戏需根据具体需求做选择。也可以采用分级策略，高中低画质分别采用不同的光照模型。