文章目录
- 2.1 数据操作
- 练习1
- 练习2
- 2.2 数据预处理
- 练习1
- 练习2
- 2.3 线性代数
- 练习1
- 练习2
- 练习3
- 练习4
- 练习5
- 练习6
- 练习7
- 练习8
- 2.4 微积分
- 练习1
- 练习2
- 练习3
- 练习4
- 2.5 自动微分
- 练习1
- 练习2
- 练习3
- 练习4
- 练习5
- 2.6 概率
- 练习1
- 练习2
- 练习2
- 练习2
2.1 数据操作
练习1
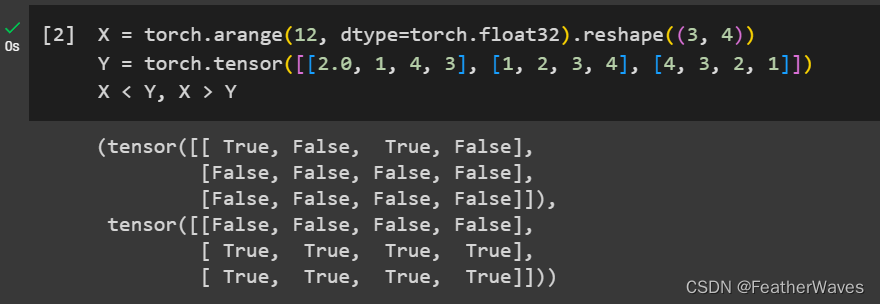
运⾏本节中的代码。将本节中的条件语句
X
=
=
Y
X == Y
X==Y更改为
X
<
Y
X < Y
X<Y或
X
>
Y
X > Y
X>Y,然后看看你可以得到什么样的张量。
练习2
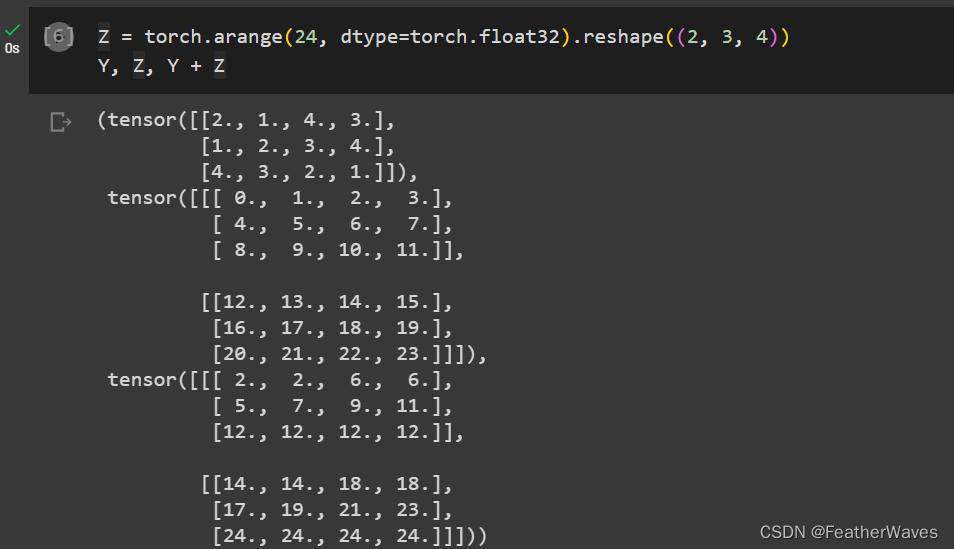
用其他形状(例如三维张量)替换⼴播机制中按元素操作的两个张量。结果是否与预期相同?
2.2 数据预处理
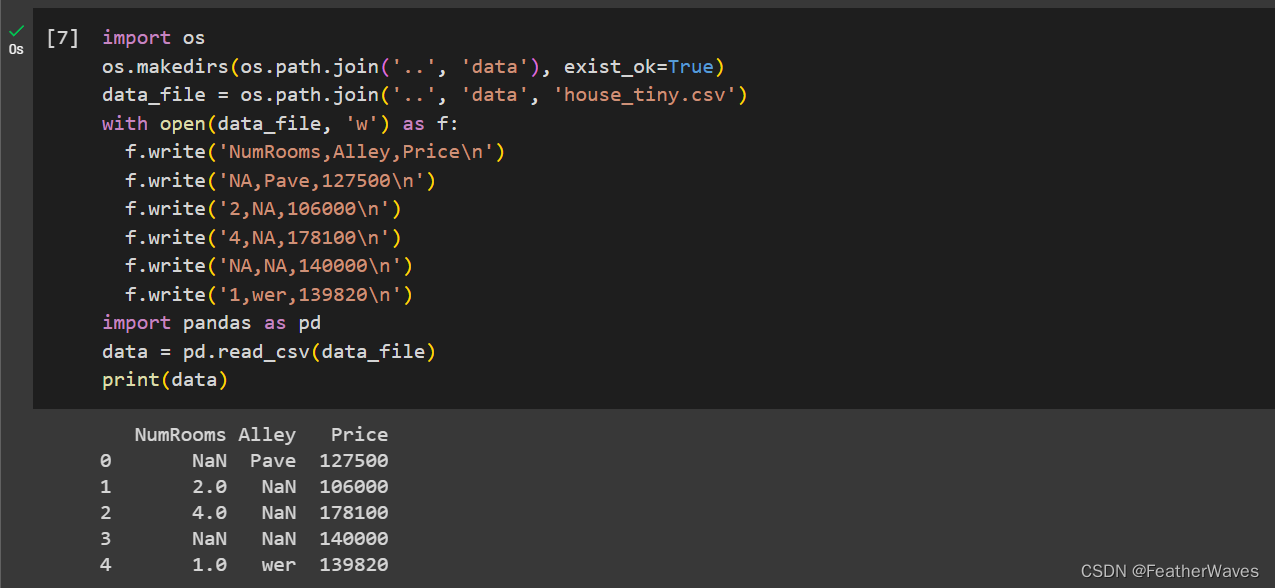
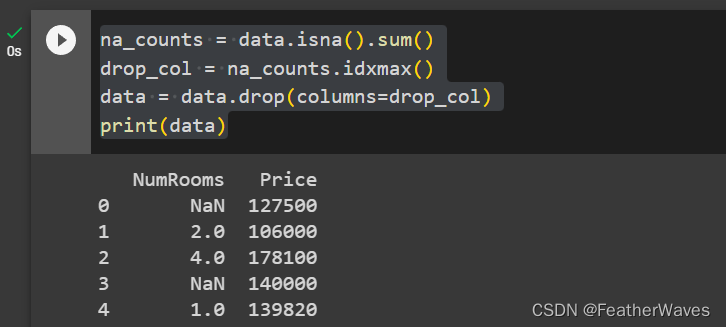
创建包含更多⾏和列的原始数据集。
- 删除缺失值最多的列。
- 将预处理后的数据集转换为张量格式。
练习1
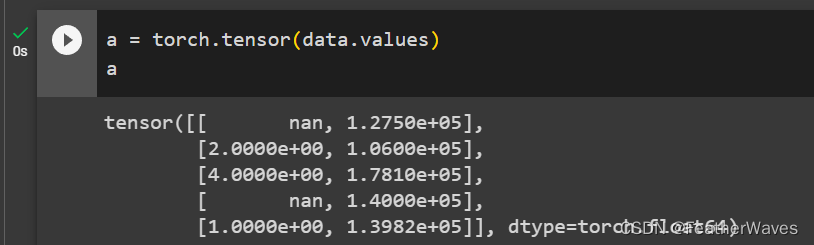
练习2
2.3 线性代数
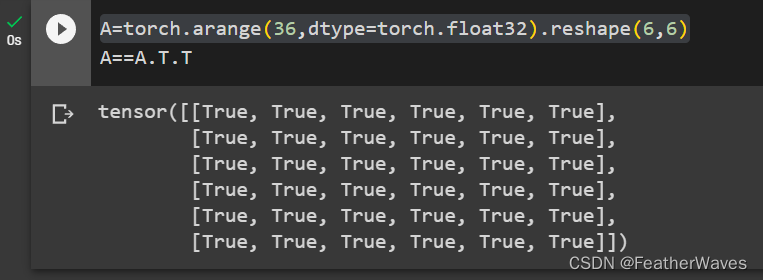
练习1
证明⼀个矩阵A的转置的转置是A,即(A⊤)⊤ = A。
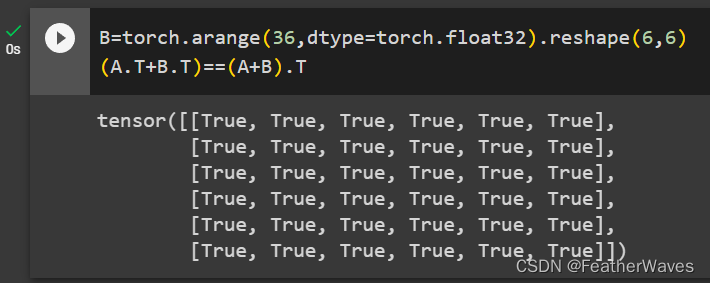
练习2
给出两个矩阵A和B,证明“它们转置的和”等于“它们和的转置”,即A⊤ + B⊤ = (A +B)⊤。
练习3
给定任意⽅阵A,A + A⊤总是对称的吗?为什么?
是的。设A是一个n×n的方阵,那么它的转置A⊤也是一个n×n的方阵,满足(A⊤)ij = Aji,其中i,j=1,2,…,n。那么A + A⊤也是一个n×n的方阵,满足(A + A⊤)ij = Aij + (A⊤)ij = Aij + Aji,其中i,j=1,2,…,n。由于(A + A⊤)ij = (A + A⊤)ji对所有的i和j都成立,所以A + A⊤是对称的。
练习4
本节中定义了形状(2, 3, 4)的张量X。len(X)的输出结果是什么?

练习5
对于任意形状的张量X,len(X)是否总是对应于X特定轴的⻓度?这个轴是什么?
对于高维张量,len()函数只能返回第一维大小,而不能返回其他维度的大小。因此,如果需要获取张量的其他维度大小,需要使用张量对象的shape属性。
练习6
运⾏A/A.sum(axis=1),看看会发⽣什么。请分析⼀下原因?
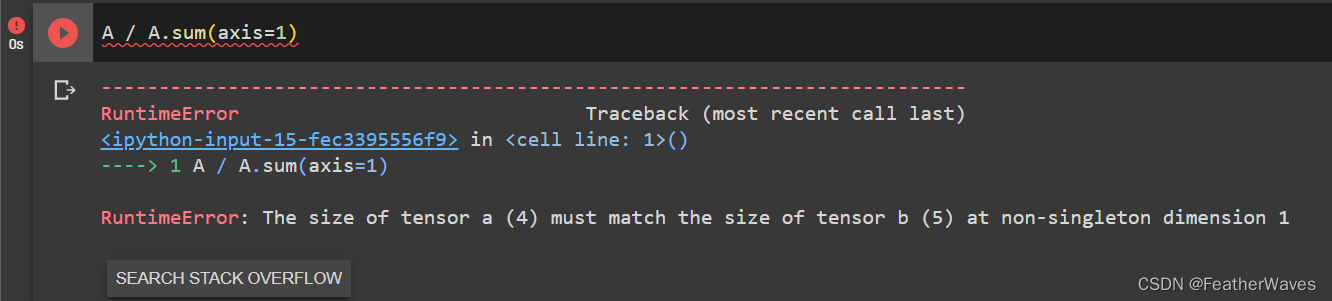
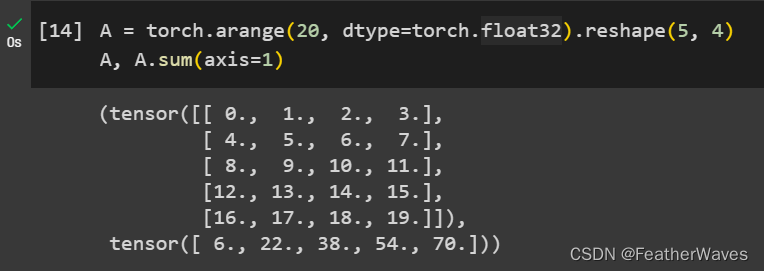
原因:这个错误出现的原因是在执行A/A.sum(axis=1)时,张量A的第一维大小为5,而A.sum(axis=1)返回的张量的第一维大小为4。由于这两个张量在第一维上的大小不同,所以无法进行逐元素的除法运算。
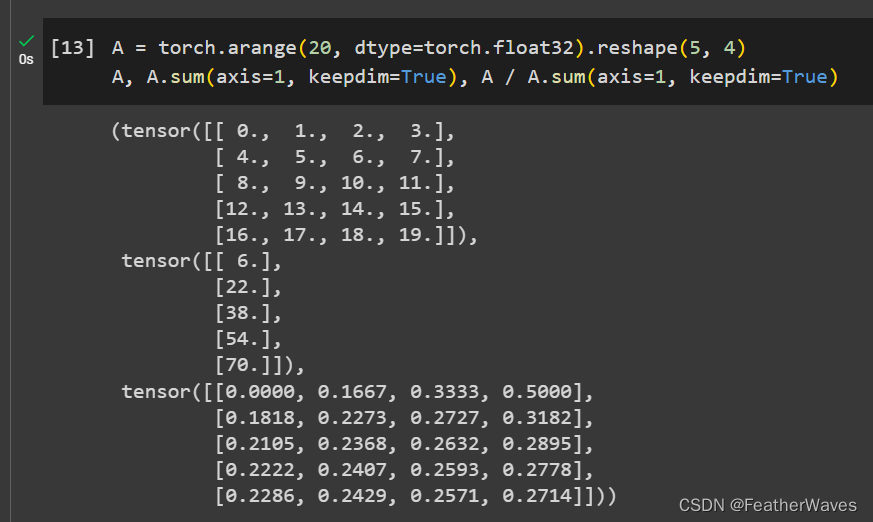
解决:要解决这个问题,需要将A.sum(axis=1)返回的张量的形状与A相同。可以通过在调用sum函数时指定参数keepdims=True来保持维度不变,然后使用broadcasting机制将A.sum(axis=1)的形状扩展为(5, 1)。
练习7
考虑⼀个具有形状
(
2
,
3
,
4
)
(2, 3, 4)
(2,3,4)的张量,在轴
0
、
1
、
2
0、1、2
0、1、2上的求和输出是什么形状?
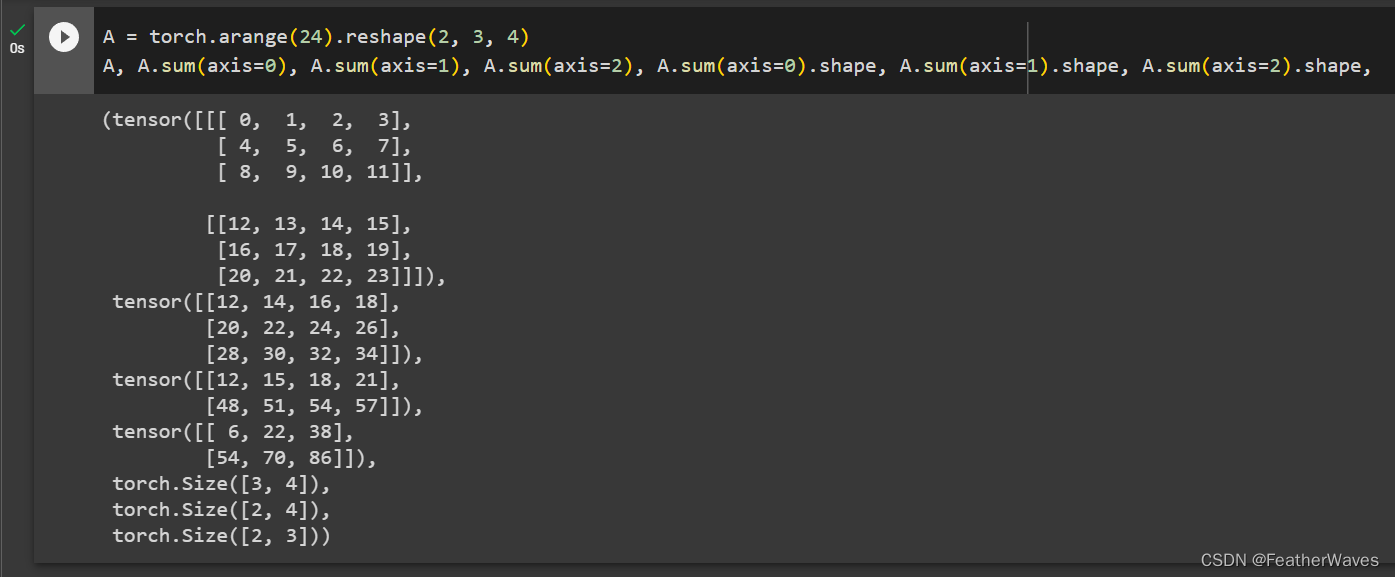
练习8
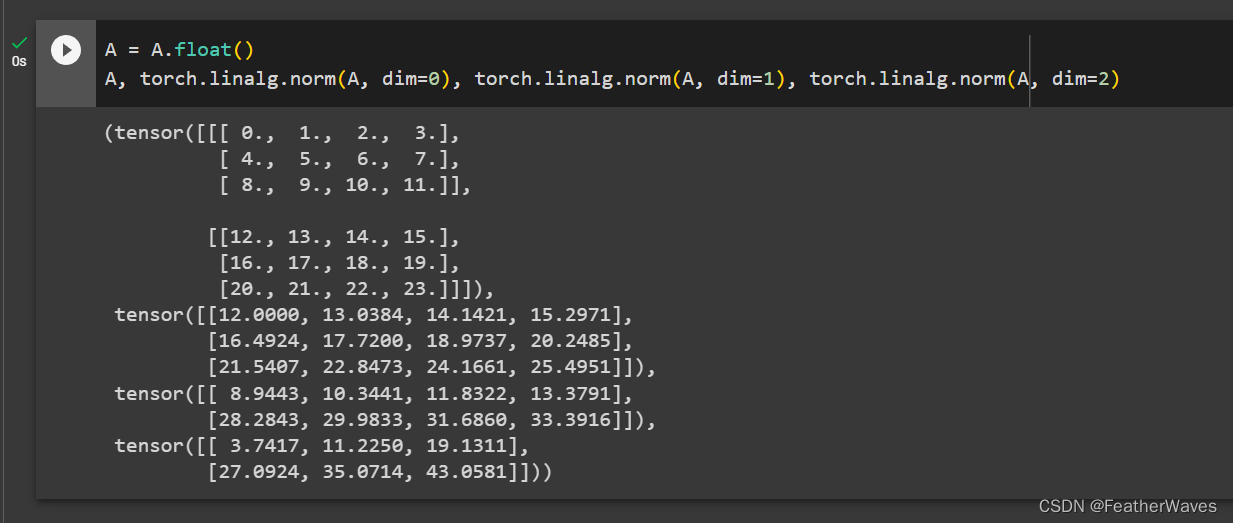
为linalg.norm函数提供3个或更多轴的张量,并观察其输出。对于任意形状的张量这个函数计算得到什么?
torch.linalg.norm函数torch.linalg.norm()函数可以用于计算张量的范数。当给定多维张量时,可以通过指定参数dim来计算指定轴上的范数。如果给定了多个轴,则会计算这些轴上的范数并返回一个形状更小的张量。
范数是一个将向量映射到非负值的函数,它度量了向量的大小或长度。在数学中,范数是一个广义的概念,包括了向量空间中的向量大小的不同度量方式。在机器学习和深度学习中,范数通常指的是向量的欧几里德范数(L2范数)和向量的曼哈顿范数(L1范数)。
范数在机器学习和深度学习中有很多应用,其中一些应用包括:
正则化:范数可以用于正则化,通过添加一个范数惩罚项来限制模型的复杂度,以避免过拟合。例如,在逻辑回归和线性回归等模型中,可以通过添加L1或L2范数惩罚项来实现正则化。
相似性度量:范数可以用于计算向量之间的相似性度量。例如,可以使用余弦相似度或欧几里德距离等度量来比较两个向量之间的相似性。
数据预处理:范数可以用于数据预处理,例如对数据进行归一化或标准化。通过将向量除以其范数,可以将向量归一化为单位向量,这有助于处理某些机器学习任务,如聚类和分类。
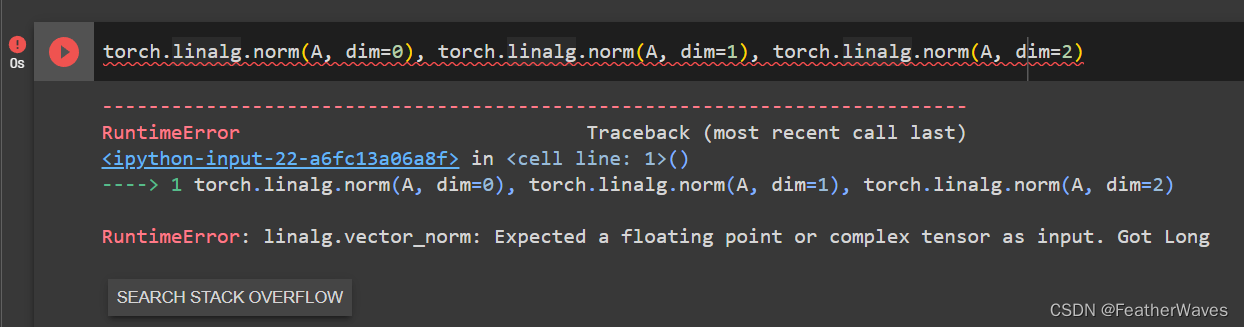
错误原因:矩阵内的数值必须为浮点数。
2.4 微积分
练习1
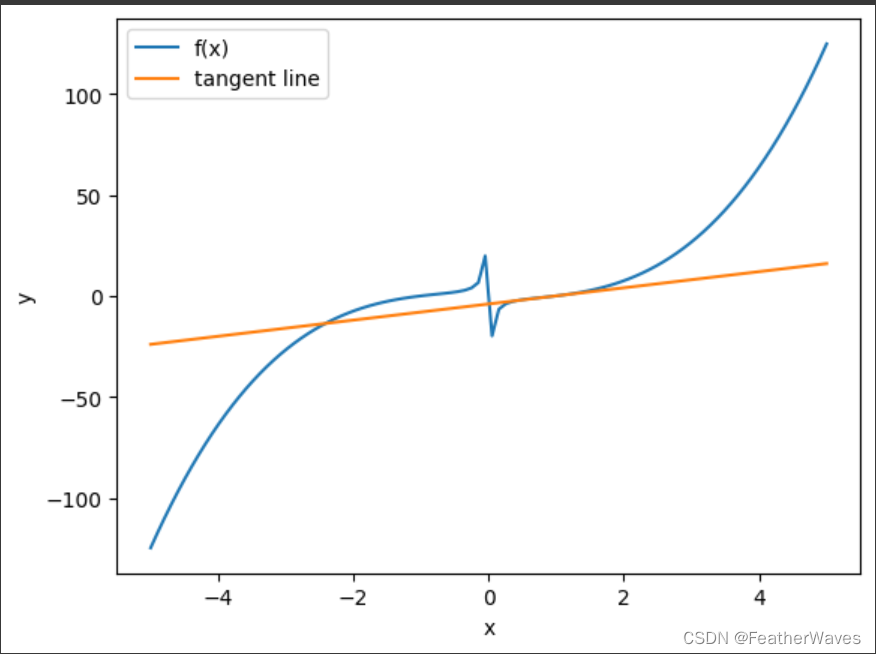
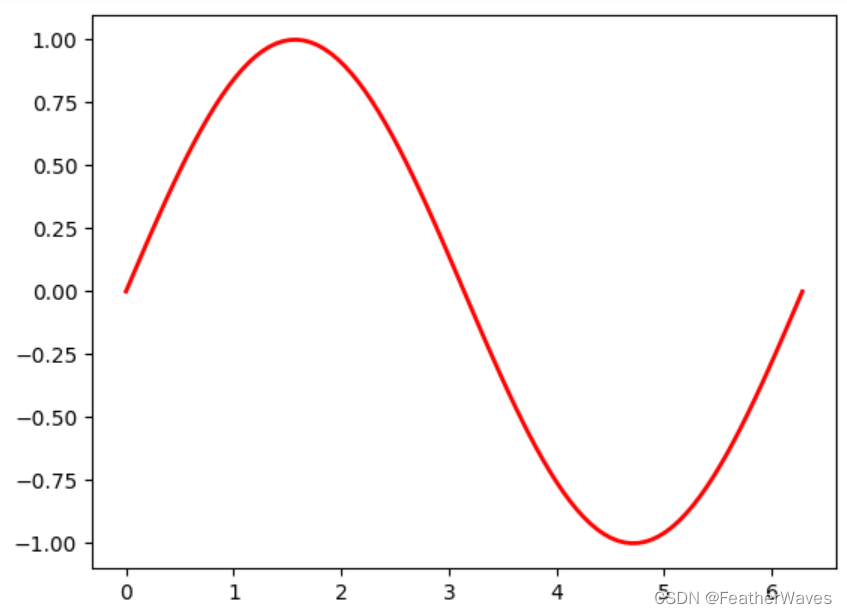
绘制函数 y = f ( x ) = x 3 − 1 x y = f(x) = x^3 −\frac{1}{x} y=f(x)=x3−x1和其在 x = 1 x = 1 x=1处切线的图像。
# 导入模块
import matplotlib.pyplot as plt
import numpy as np
# 定义函数和导数
def f(x):
return x**3 - 1/x
def f_prime(x):
return 3*x**2 + 1/x**2
# 生成x值的数组
x = np.linspace(-5, 5, 100)
# 计算y值和切线斜率的数组
y = f(x)
m = f_prime(x)
# 绘制函数曲线
plt.plot(x, y, label="f(x)")
# 绘制切线
# 切点的x坐标
x0 = 1
# 切点的y坐标
y0 = f(x0)
# 切线的斜率
m0 = f_prime(x0)
# 切线的截距
b0 = y0 - m0 * x0
# 切线的方程
def tangent_line(x):
return m0 * x + b0
# 切线的y值的数组
y_tangent = tangent_line(x)
# 绘制切线
plt.plot(x, y_tangent, label="tangent line")
# 显示图像
plt.xlabel("x")
plt.ylabel("y")
plt.legend()
plt.show()
练习2
求函数 f ( x ) = 3 x 1 2 + 5 e x 2 f(x) = 3x_1^2 + 5e^{x_2} f(x)=3x12+5ex2的梯度。
梯度为: ( 6 x 1 , 5 e X 2 ) (6x_1, 5e^{X_2}) (6x1,5eX2)
练习3
函数 f ( x ) = ∥ x ∥ 2 f(x) = ∥x∥_2 f(x)=∥x∥2的梯度是什么?
范数: ∣ ∣ x ∣ ∣ ||x|| ∣∣x∣∣表示 x x x的范数,也就是 x x x的长度或大小。
∣ ∣ X ∣ ∣ 2 ||X||_2 ∣∣X∣∣2为第二范数
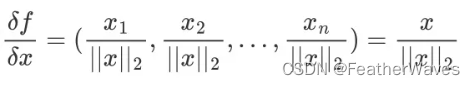
练习4
尝试写出函数
u
=
f
(
x
,
y
,
z
)
u = f(x, y, z)
u=f(x,y,z),其中
x
=
x
(
a
,
b
)
,
y
=
y
(
a
,
b
)
,
z
=
z
(
a
,
b
)
x = x(a, b),y = y(a, b),z = z(a, b)
x=x(a,b),y=y(a,b),z=z(a,b)的链式法则。
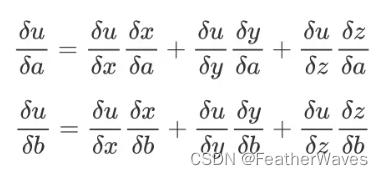
2.5 自动微分
练习1
为什么计算⼆阶导数⽐⼀阶导数的开销要更⼤?
因为计算二阶导数要在一阶导数的基础上再进行求导,这就需要构建新的计算图,保存更多的中间结果,占用更多的内存和计算资源。而计算一阶导数只需要沿着原有的计算图反向传播梯度值,不需要额外的开销。
练习2
在运⾏反向传播函数之后,⽴即再次运⾏它,看看会发⽣什么。
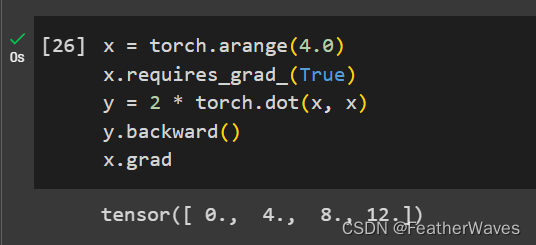
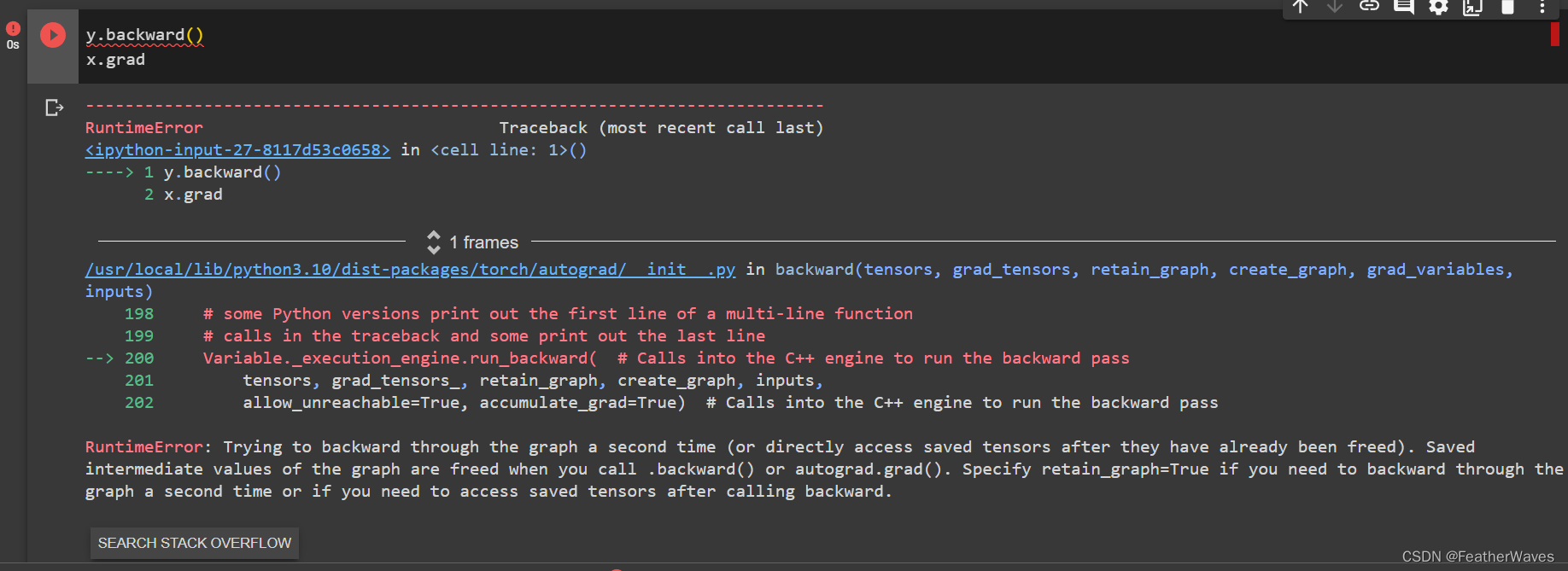
这意味着你试图对一个已经释放了计算图的张量进行反向传播,这是不允许的。当你调用.backward()或autograd.grad()时,计算图中的中间值会被释放,以节省内存。如果你需要对同一个张量进行第二次反向传播或者在调用.backward()后访问保存的张量,你需要在第一次调用.backward()时指定retain_graph=True参数,以保留计算图。
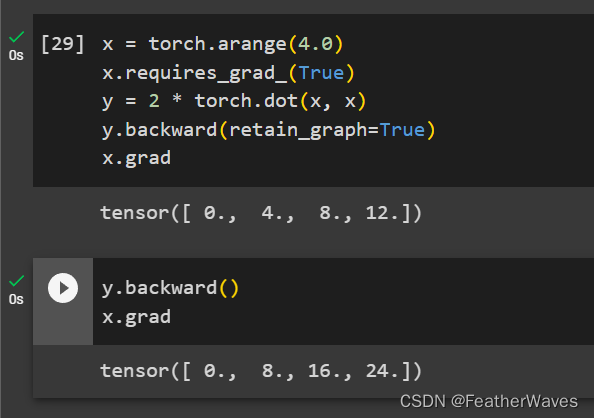
练习3
在控制流的例⼦中,我们计算d关于a的导数,如果将变量a更改为随机向量或矩阵,会发⽣什么?
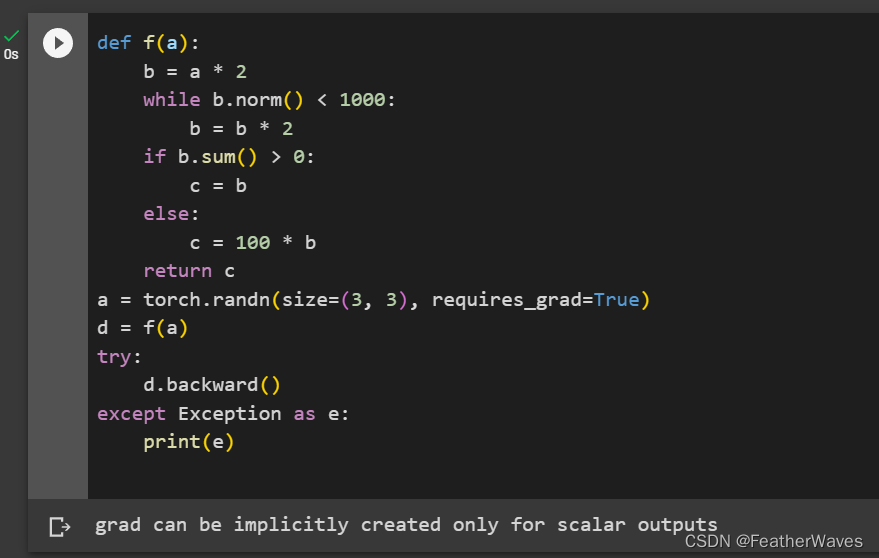
在调用backward()方法之前,需要确保输出张量是一个标量,否则将会引发与之类似的错误。
在PyTorch中,计算图是动态构建的,即在每次计算中重新构建一次计算图。因此,将张量作为函数的输出时,需要指定一个标量值作为损失函数,以便计算梯度。反向传播的过程是从损失函数开始,逐步向前计算每个计算步骤的梯度,直到达到需要求解的变量为止。因此,反向传播的计算过程必须以标量输出为起点。
在PyTorch中,如果将一个非标量张量作为函数的输出,那么在调用backward()方法时,将会收到一个RuntimeError异常,提示"grad can be implicitly created only for scalar outputs"。这是因为计算梯度需要沿着计算图向后传播,而非标量输出会导致计算图的多个分支汇聚在一起,无法确定要计算哪个分支的梯度,因此无法正确计算梯度。
因此,为了进行反向传播,需要将输出张量降维为标量,以便能够计算梯度。在降维过程中,可以使用一些常见的降维函数,如mean()、sum()等,将张量的所有元素合并为一个标量。
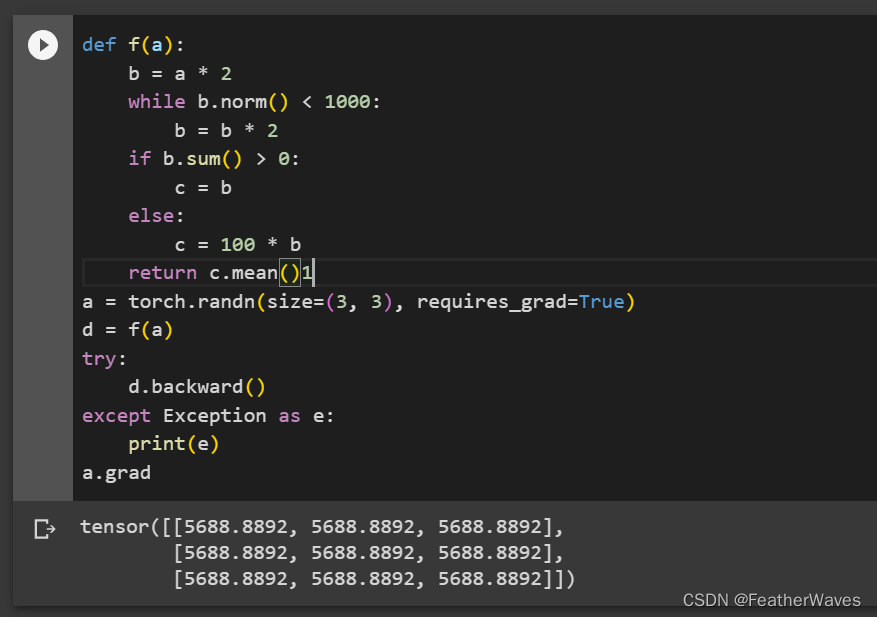
练习4
重新设计⼀个求控制流梯度的例⼦,运⾏并分析结果。
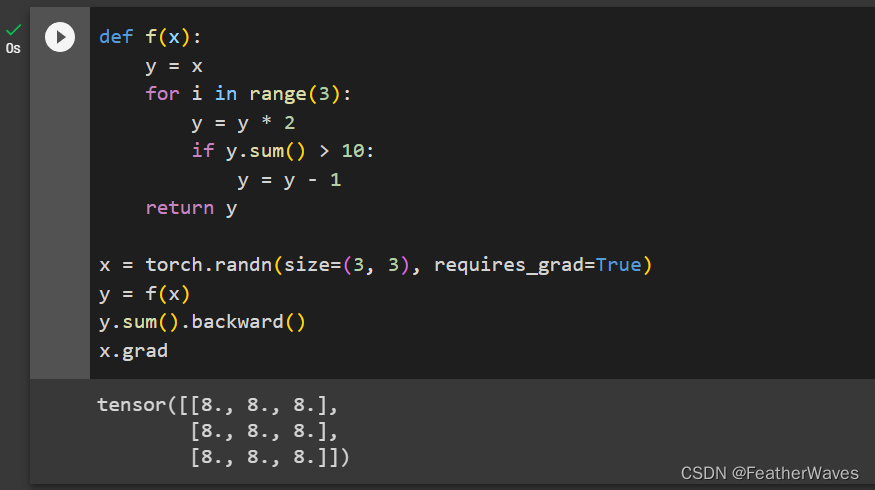
这段代码定义了一个函数f(x),它接受一个三行三列的张量x作为输入,然后对x进行三次循环,每次循环都把x乘以2,如果x的元素之和大于10,就把x的每个元素减去1,最后返回x。然后,它创建了一个随机生成的三行三列的张量x,并且设置了requires_grad为True,表示需要计算x的梯度。接着,它调用f(x)得到y,并对y的元素之和求导,得到x的梯度。最后,它打印出x的梯度。
结果显示,x的梯度是一个全为8的三行三列的张量。这是因为y是x的线性函数,
y
=
8
x
−
c
y = 8x - c
y=8x−c,其中c是一个常数。因此,y对x的偏导数就是8。当我们对y的元素之和求导时,相当于对每个元素求导再求和,所以结果就是8乘以9(元素个数),即72。由于我们使用了backward()方法,它会自动把72分配给每个元素,所以x的梯度就是全为8的张量。
练习5
使
f
(
x
)
=
s
i
n
(
x
)
f(x) = sin(x)
f(x)=sin(x),绘制
f
(
x
)
f(x)
f(x)和
d
f
(
x
)
d
x
\frac{df(x)}{dx}
dxdf(x)的图像,其中后者不使⽤
f
(
x
)
=
c
o
s
(
x
)
f(x) = cos(x)
f(x)=cos(x)。
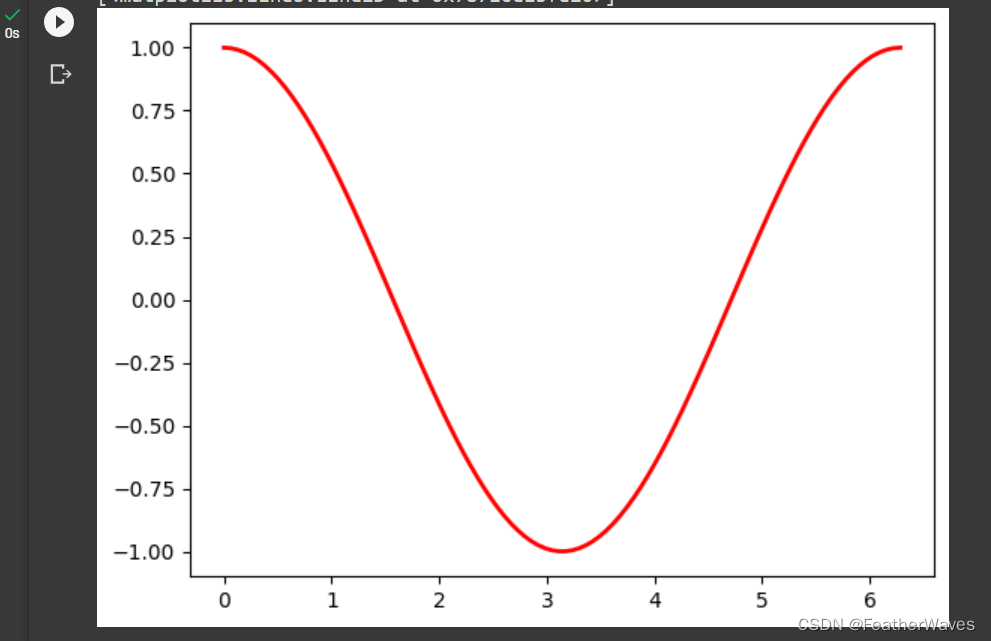
2.6 概率
练习1
进⾏
m
=
500
m = 500
m=500组实验,每组抽取
n
=
10
n = 10
n=10个样本。改变
m
m
m和
n
n
n,观察和分析实验结果。
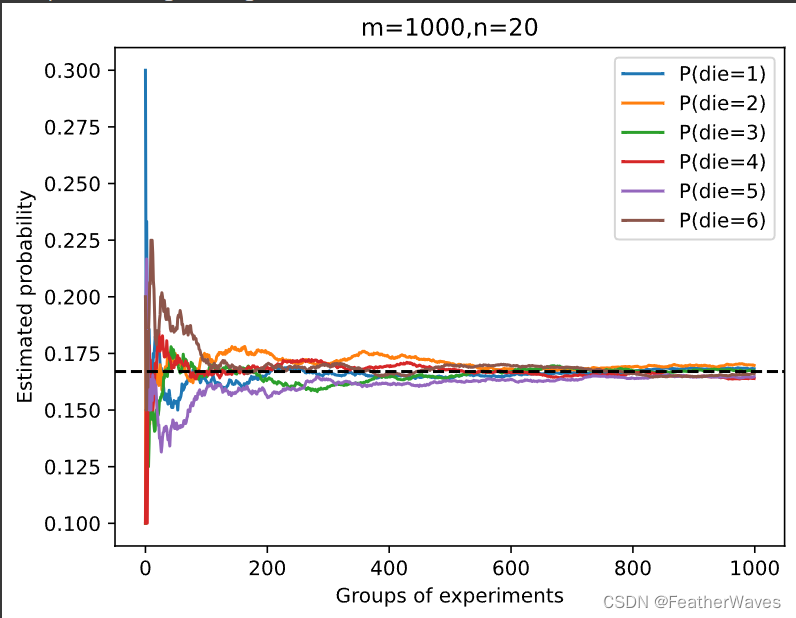
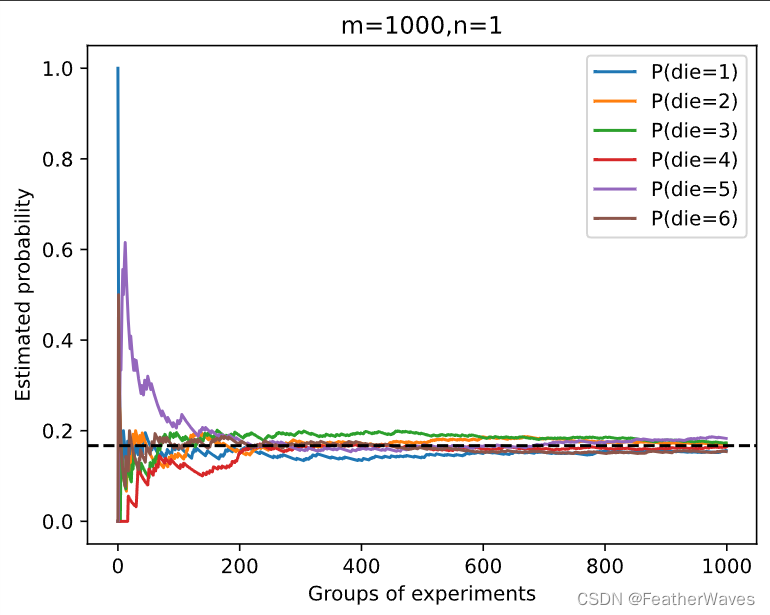
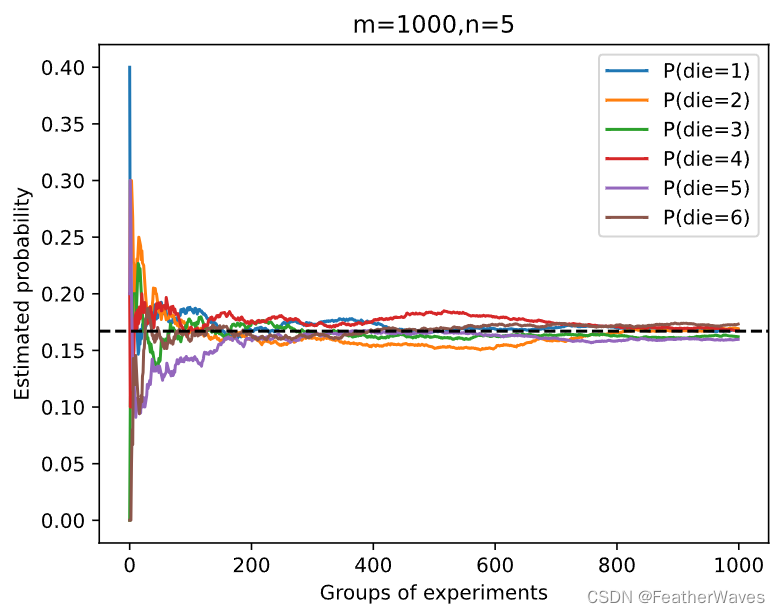
练习2
给定两个概率为 P ( A ) P(A) P(A)和 P ( B ) P(B) P(B)的事件,计算 P ( A ∪ B ) P(A ∪ B) P(A∪B)和 P ( A ∩ B ) P(A ∩ B) P(A∩B)的上限和下限。(提示:使⽤友元图来展示这些情况。)
P
(
A
∪
B
)
P(A ∪ B)
P(A∪B)的上限以及
P
(
A
∩
B
)
P(A ∩ B)
P(A∩B)的下限:
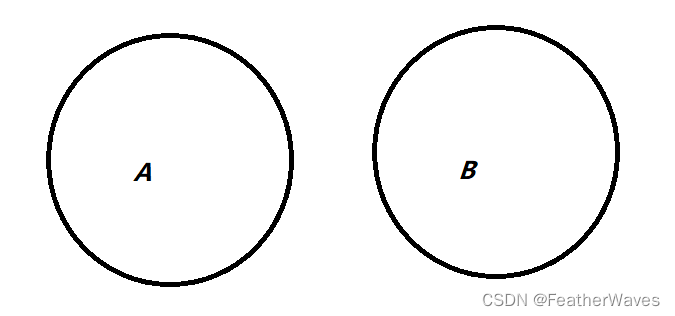
P
(
A
∪
B
)
P(A ∪ B)
P(A∪B)的下限以及
P
(
A
∩
B
)
P(A ∩ B)
P(A∩B)的上限:
练习2
假设我们有⼀系列随机变量,例如 A 、 B A、B A、B和 C C C,其中 B B B只依赖于 A A A,⽽ C C C只依赖于 B B B,能简化联合概率 P ( A , B , C ) P(A, B, C) P(A,B,C)吗?(提⽰:这是⼀个马尔可夫链。)
由于B只依赖于A,可知
P
(
B
∣
A
,
C
)
=
P
(
B
∣
A
)
P(B|A, C) = P(B|A)
P(B∣A,C)=P(B∣A)
由于B只依赖于A,可知
P
(
C
∣
A
,
B
)
=
P
(
C
∣
B
)
P(C|A, B) = P(C|B)
P(C∣A,B)=P(C∣B)
可得:
P
(
A
,
B
,
C
)
=
P
(
C
∣
A
,
B
)
P
(
A
,
B
)
=
P
(
C
∣
A
,
B
)
P
(
B
∣
A
)
P
(
A
)
=
P
(
C
∣
B
)
P
(
B
∣
A
)
P
(
A
)
\begin{aligned} P(A, B, C)&= P(C|A, B)P(A, B)\\ &=P(C|A, B)P(B|A)P(A)\\ &=P(C|B)P(B|A)P(A) \end{aligned}
P(A,B,C)=P(C∣A,B)P(A,B)=P(C∣A,B)P(B∣A)P(A)=P(C∣B)P(B∣A)P(A)
练习2
在 2.6.2节中,第⼀个测试更准确。为什么不运⾏第⼀个测试两次,⽽是同时运⾏第⼀个和第⼆个测试?
现实中我们不会让病人进行两次同种检验,另外如果进行相继两次的第一种测试,得到都为阳性的结果患者得病的概率为 1 − ( 1 − 0.1307 ) 2 = 0.24431751000000002 1-(1-0.1307)^2=0.24431751000000002 1−(1−0.1307)2=0.24431751000000002,更加不现实了。