题目

在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组，求出这个数组中的逆序对的总数。

示例 1:

解题思路

前置知识

分治法
设计思想：
将规模为n的问题分解为k个规模较小的子问题，这些子问题互相独立且与原问题形式相同，递归地解这些子问题，然后将各子问题的解合并得到原问题的解。

分治法所能解决的问题一般具有以下几个特征：

该问题的规模缩小到一定的程度就可以容易地解决。
该问题可以分解为若干个规模较小的相同问题。
利用该问题分解出的子问题的解可以合并为该问题的解。
该问题所分解出的各个子问题是相互独立的，即子问题之间不包含公共的子问题。

求解步骤：

分解：将原问题分解为若干个规模较小，相互独立，与原问题形式相同的子问题。
求解子问题：若子问题规模较小而容易被解决则直接求解，否则递归地求解各个子问题。
合并：将各个子问题的解合并为原问题的解。

大概知道了分治法的思想后，我们来一起看一下这道题

1.题目要求我们求出所给数组中的逆序对，我们首先想到的方法可能是去暴力求解，也就是两个for循环去两两比较，但是这种方法会超出时间限制。所以我们换一种思路，利用分治法来解决问题，为了能够更好的理解，我用图片的形式来讲述。

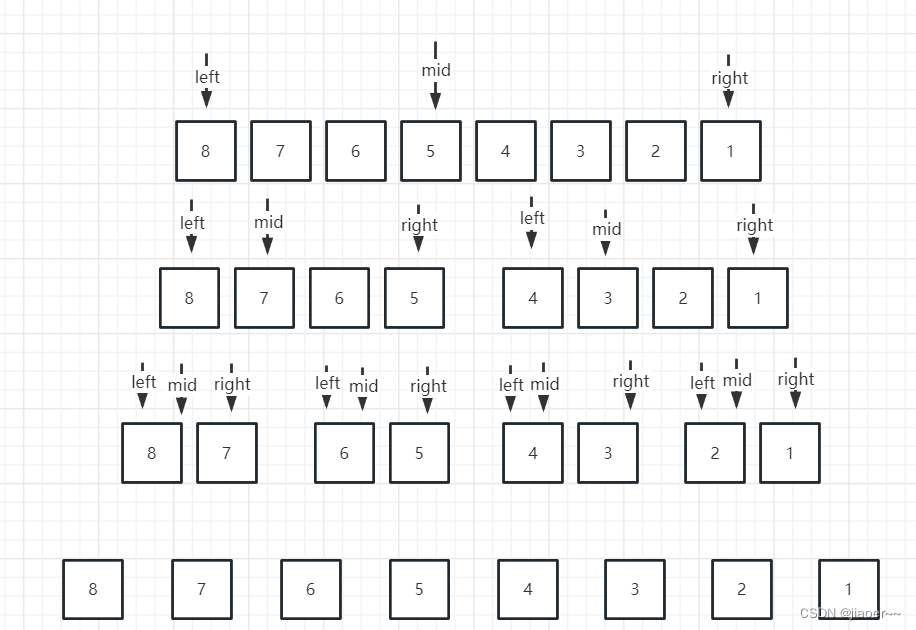
2.下面我们来举一个最极限的栗子：[8,7,6,4,3,2,1]

这个数组中的每一个数都与后面的数形成逆序对

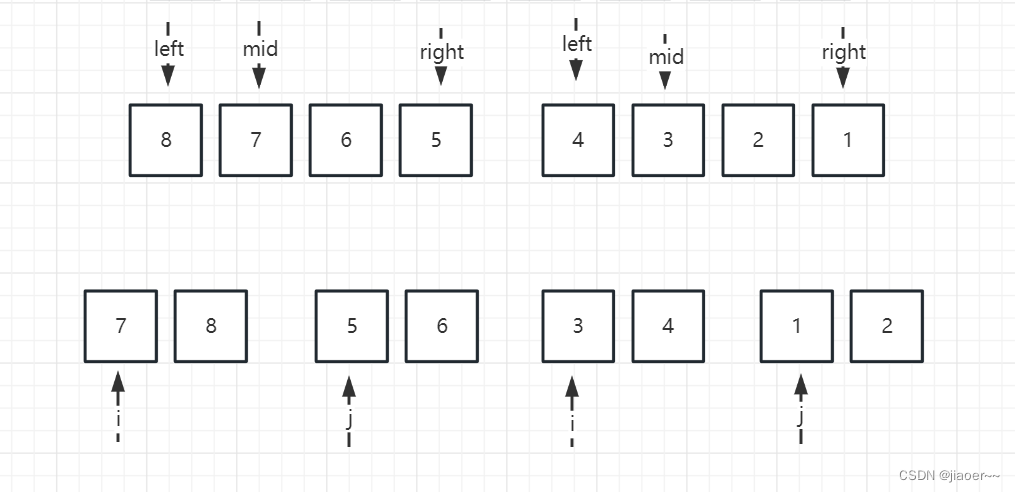
分治的思想就是要把一个问题拆分为k个规模较小的问题，所以我们以二分的形式对数组进行拆分。

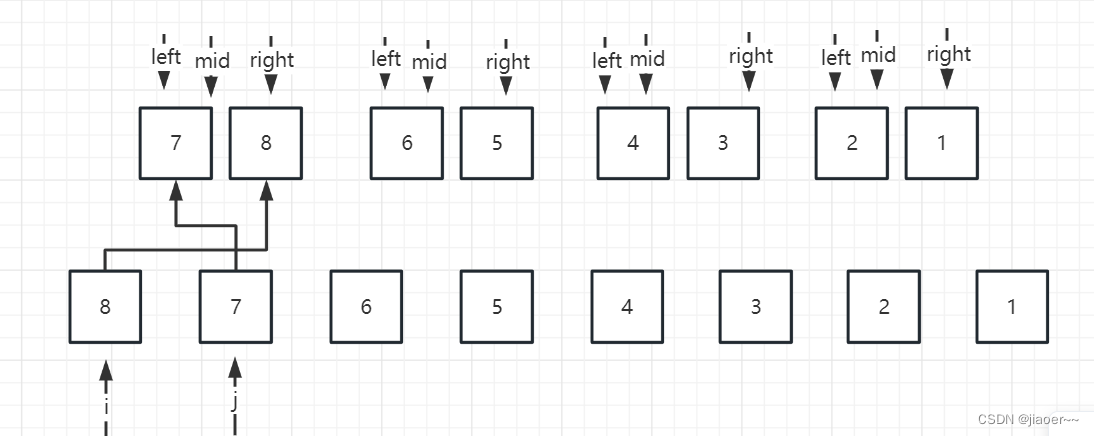
计算逆序对的数量的操作就发生在我们的合并过程中，首先我们让 i = left，j = mid + 1，

当 i > j 时，我们就将 j 先排进数组，此时我们发现 i 指向的数组中存在一个比 j 大的元素，也就是说 7 之前存在一个 8 比它大，那么我们就应该设置一个count，让它加一来记录下这个逆序对

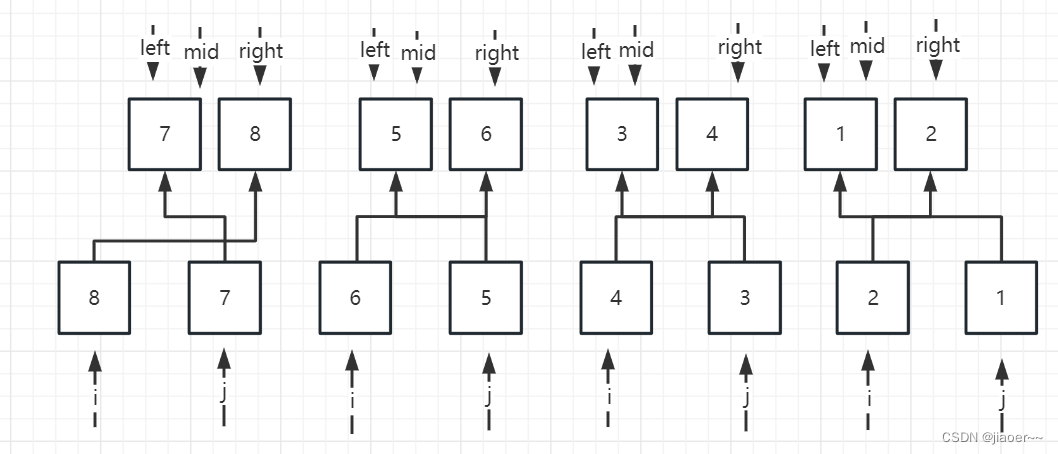
同理可得，合并完第一次后，我们的count计算器就变为了4，还生成了4个新的有序数组

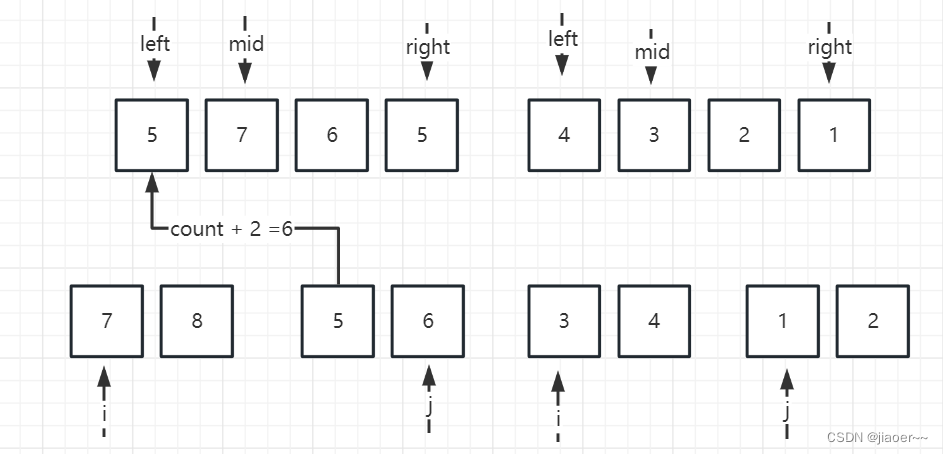
此时我们依旧让i = left，j = mid + 1，然后比较 i 和 j 的大小，若 i < j ，那么就让 i 直接排进数组，若 i > j，那么我们就需要计算出 i 所指向的数组中所剩的元素，因为当 i > j 时，j 所指向的元素比 i 所指向的有序数组中的最小的元素还要小，那么 j 必然跟 i 所指向的数组中所剩的所有元素构成逆序对，所以我们要计算出 i 所指向的数组中所剩的元素个数并于count 相加

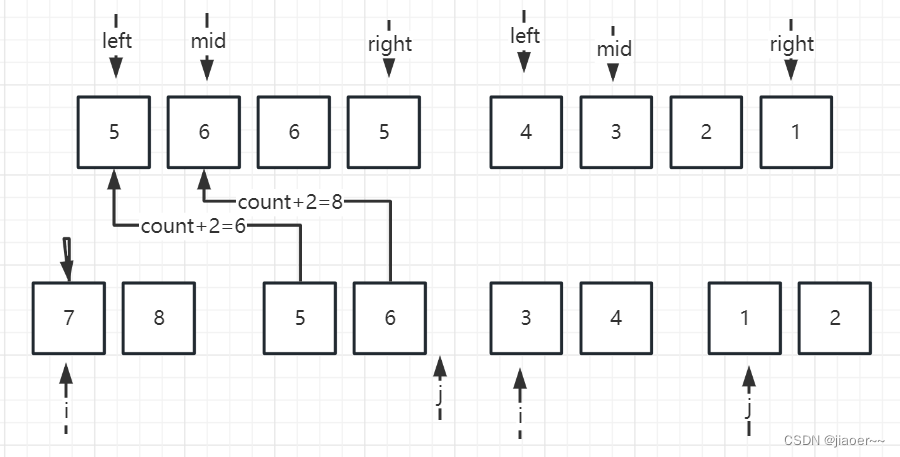
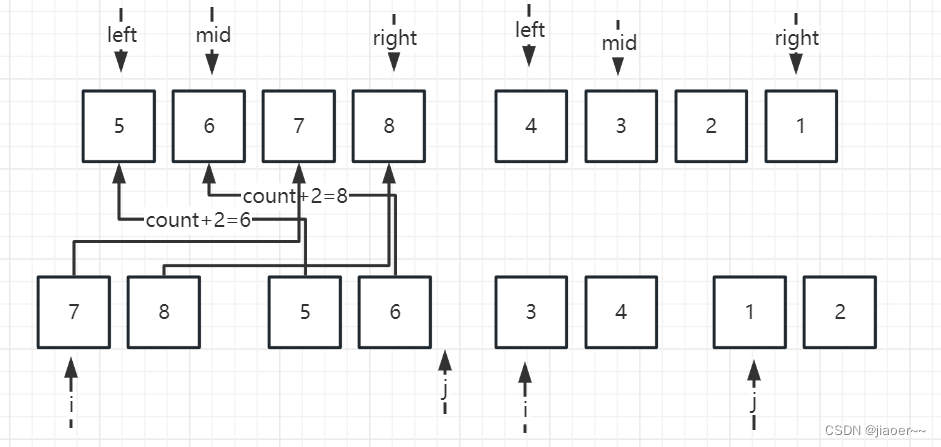
此时 j 指向的数组已经为空，我们只需要将 i 所指向的数组排入即可

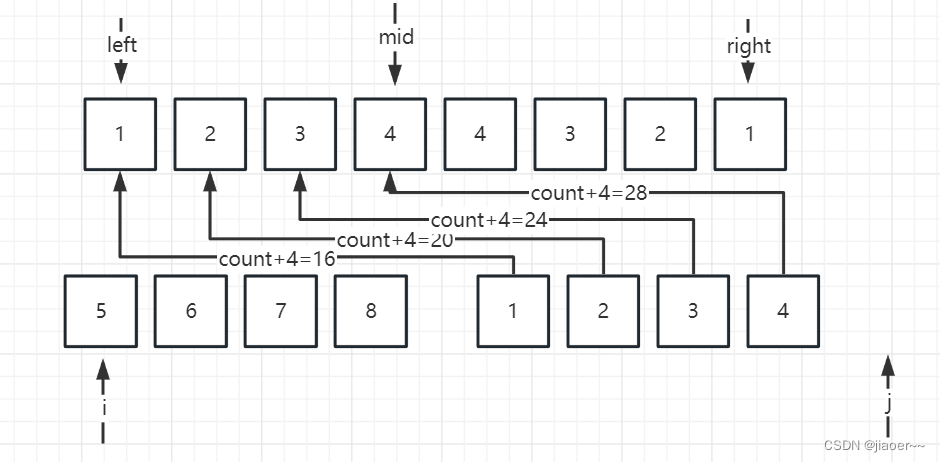
此时 j 所指向的数组已经遍历结束，我们将 i 指向的数组排入即可

至此，我们就统计了此数组中所存在的逆序对个数。

代码实现

class Solution {
    public int reversePairs(int[] nums) {
        int len = nums.length;
        if(len < 2){
            return 0;
        }
        int[] copy = new int[len];
        for(int i = 0; i < len; i++){
            copy[i] = nums[i];
        }
        int[] temp = new int[len];
        return reversePairs(copy, 0, len - 1, temp);

    }
    private int reversePairs(int [] nums, int left, int right, int[] temp){
        if(left == right){
            return 0;
    }
    int mid = left + (right - left) / 2;
    int leftnum = reversePairs(nums, left, mid, temp);
    int rightnum = reversePairs(nums, mid + 1, right, temp);
    if(nums[mid] <= nums[mid + 1]){
        return leftnum + rightnum;
    }
    int combine = merge(nums, left, mid, right, temp);
    return combine + leftnum + rightnum;
}
    private int merge(int[] nums, int left, int mid, int right, int[] temp){
        for(int i = left; i <= right; i++){
            temp[i] = nums[i];
        }
        int i = left;
        int j = mid + 1;

        int count = 0;
        for(int k = left; k <= right; k++){
            if(i == mid + 1){
                nums[k] = temp[j];
                j++;
            }else if(j == right + 1){
                nums[k] = temp[i];
                i++;
            }else if(temp[i] <= temp[j]){
                nums[k] = temp[i];
                i++;
            }else{
                nums[k] = temp[j];
                j++;
                count += (mid - i + 1);
            }
        }
        return count;
    }
    
}