今天采用前作者自行改进的一个算法---融合正余弦和折射反向学习的北方苍鹰(SCNGO)优化算法优化BP神经网络。

文章一次性讲解两种案例，回归与分类。回归案例中，作者选用了一个经典的股票数据。分类案例中，选用的是公用的UCI数据集。

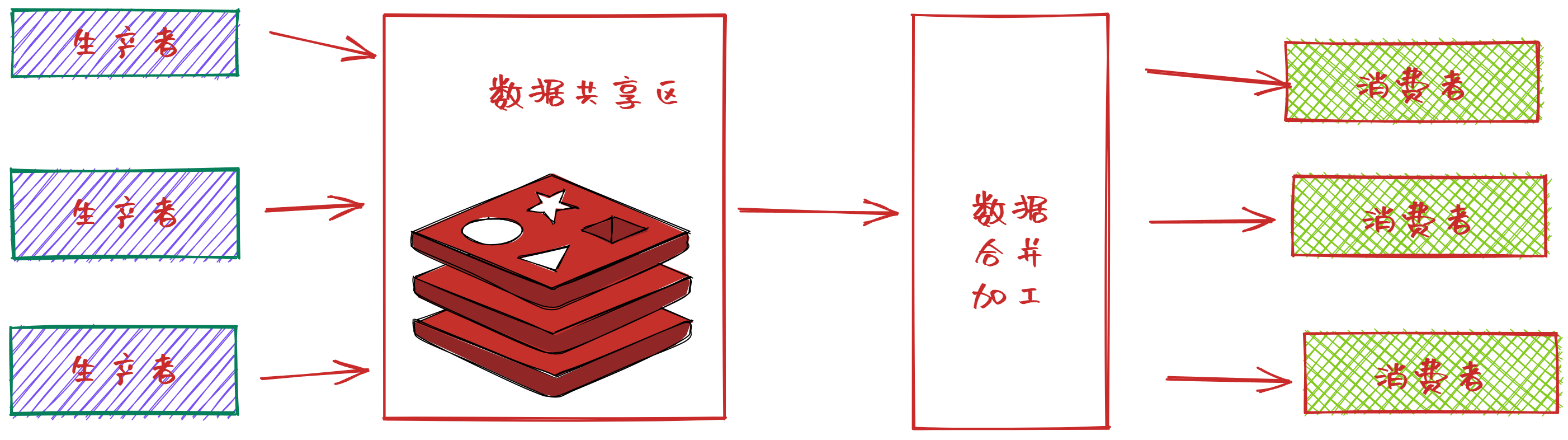
BP神经网络初始的权值阈值都是随机生成的，因此不一定是最佳的。采用智能算法优化BP神经网络的权值阈值，使得输入与输出有更加完美的映射关系，以此来提升BP神经网络模型的精度。本文采用SCNGO算法对BP神经网络的权值阈值进行优化，并应用于实际的回归和分类案例中。

01 股票预测案例

案例虽然介绍的是股票预测，但是SCNGO-BP预测模型是通用的，大家根据自己的数据直接替换即可。

股票数据特征有：开盘价，盘中最高价，盘中最低价，收盘价等。预测值为股票价格。股票数据整理代码已写好，想换成自己数据的童鞋不需要理解此代码，替换数据即可。下面直接上标准BP的预测结果和SCNGO-BP的预测结果。

标准BP模型预测结果：

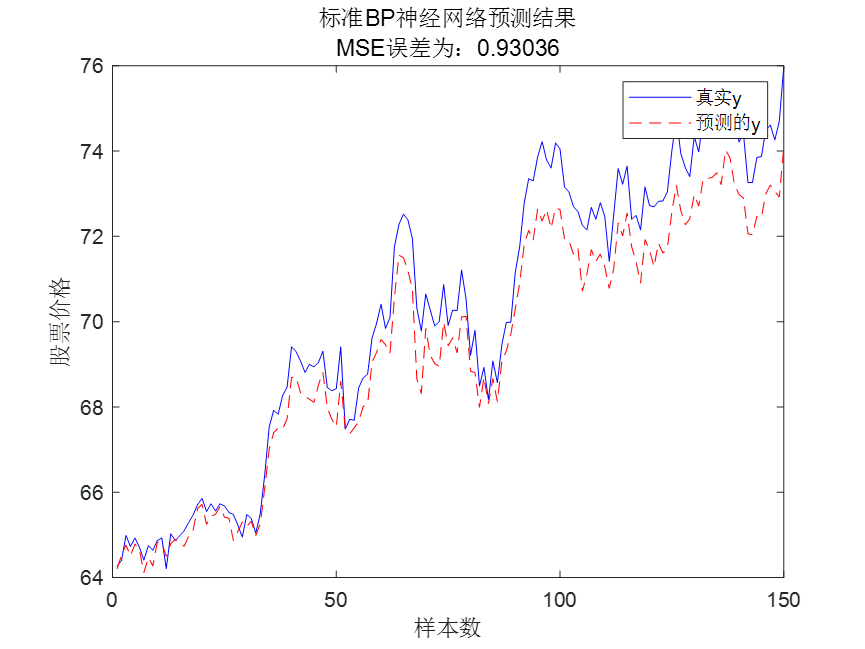
可以看到标准BP神经网络的预测效果不是很理想，无法跟踪真实值，偏差较大。

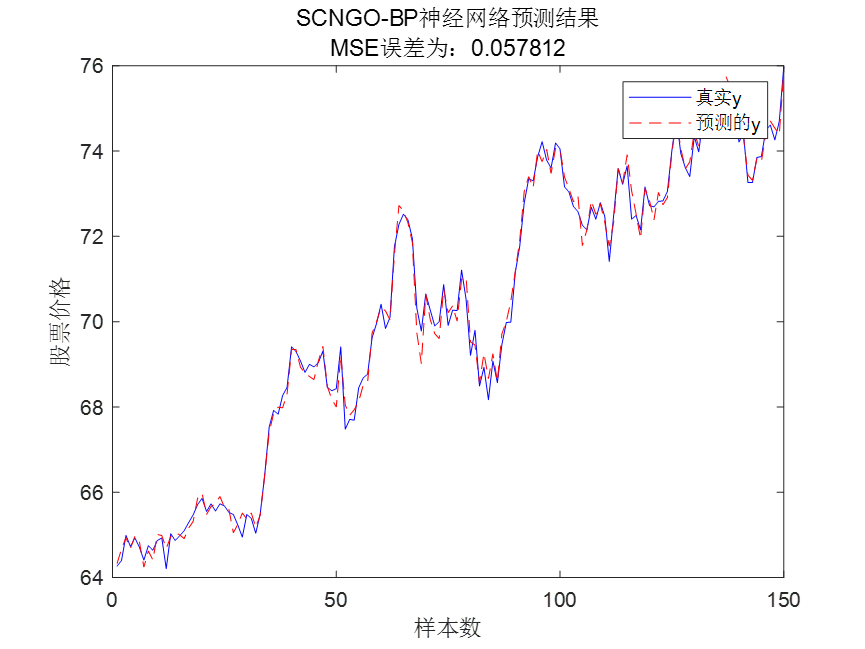
SCNGO-BP预测结果：

可以看到SCNGO-BP神经网络的预测值可以紧密跟随真实值，效果很好。

将真实值，BP预测值和SCNGO-BP预测值放在一起，效果更加明显。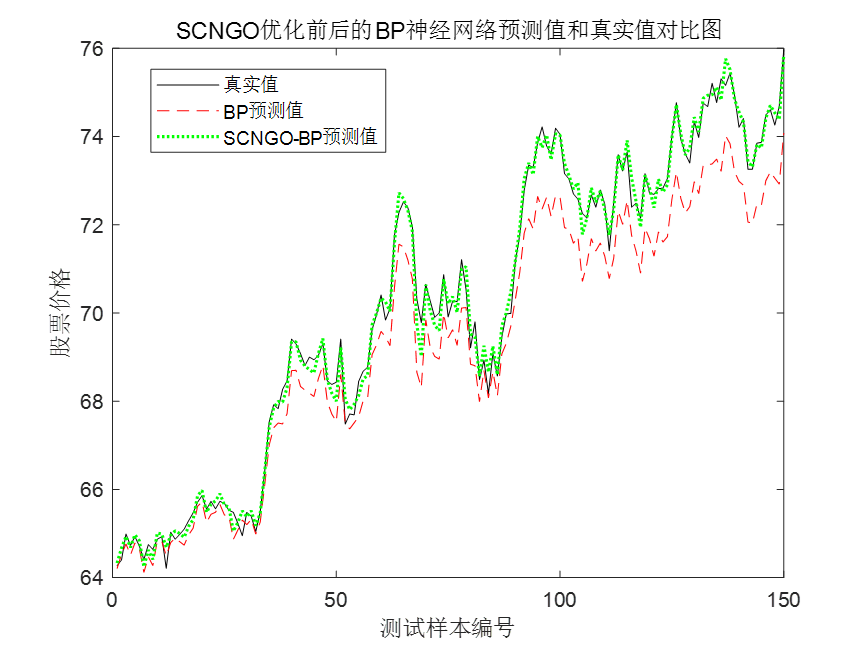

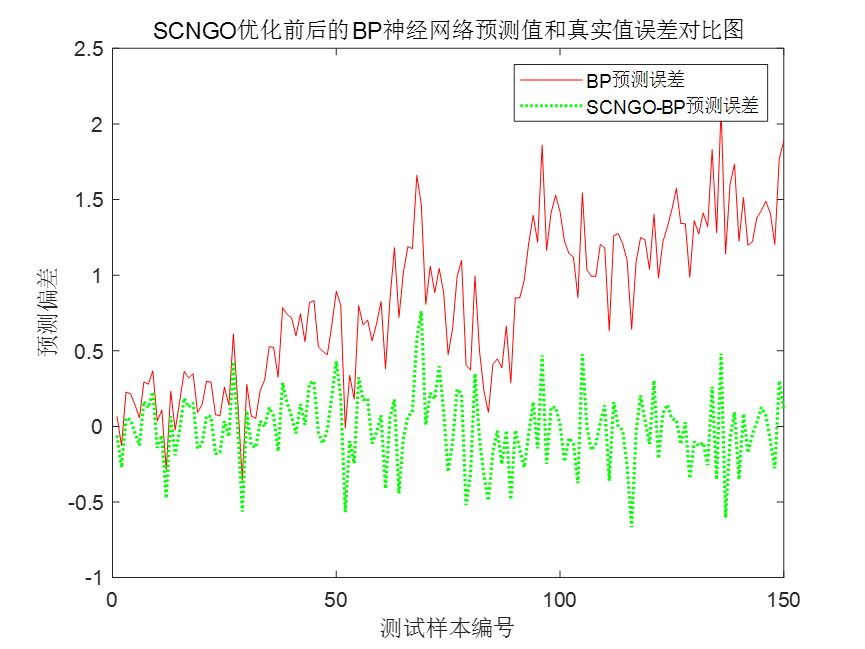
接下来是一个SCNGO优化前后的BP神经网络误差对比图。

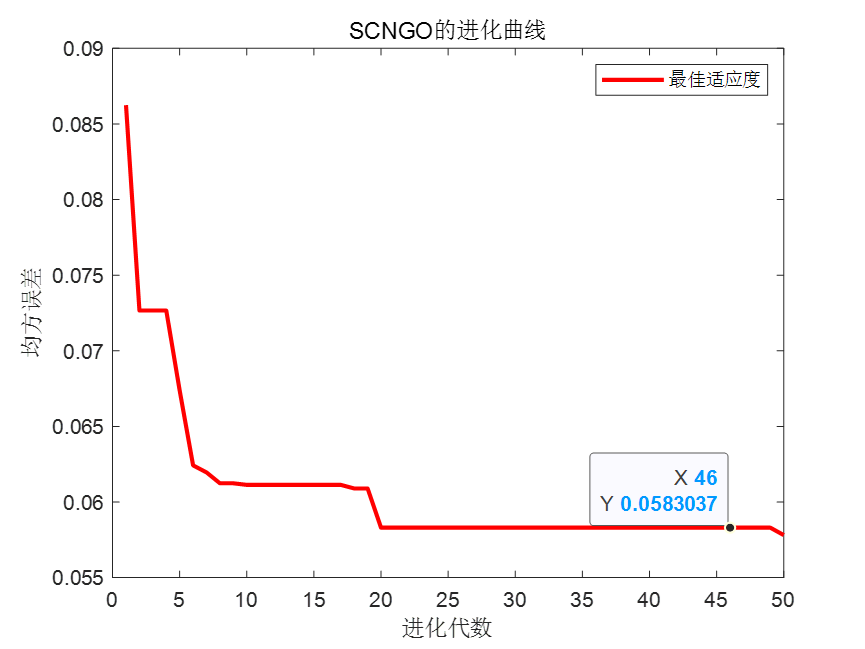
SCNGO-BP的迭代曲线，以预测值和真实值的MSE为目标函数。

SCNGO-BP预测模型的评价：可以看到，SCNGO-BP方法在股票预测案例中可以很好地进行股票价格预测。

02 分类案例

接下来是SCNGO-BP的分类案例，采用的数据是UCI数据集中的Balancescale.mat数据，该数据一共分为三类。接下来看结果。

标准BP模型分类结果：

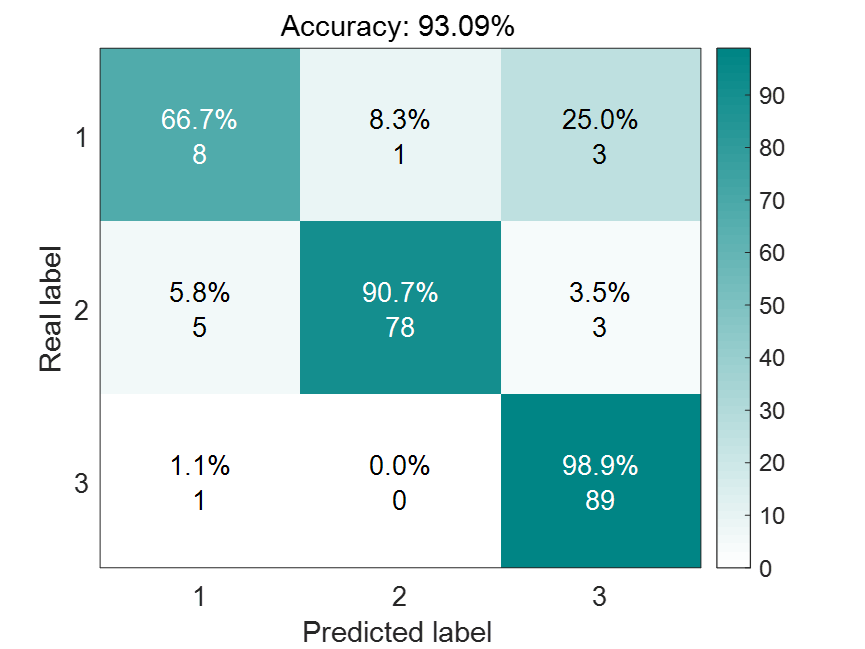
混淆矩阵结果图：

简单说一下这个图该怎么理解。请大家横着看，每行的数据加起来是100%，每行的数据个数加起来就是测试集中第一类数据的真实个数。以第一行为例，测试集中一共有12个数据是属于第一类的，而12个数据中，有8个预测正确，有1个预测成了第2类，3个预测成了第三类。其他行均这样理解。

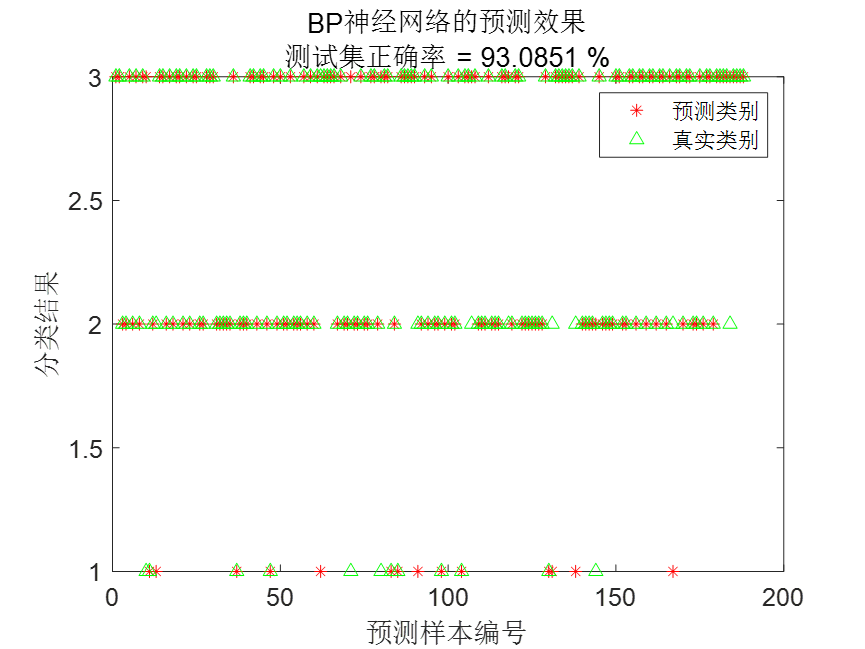
下面这个图是另一种结果展现方式，在一些论文中会用这种方式展示结果。

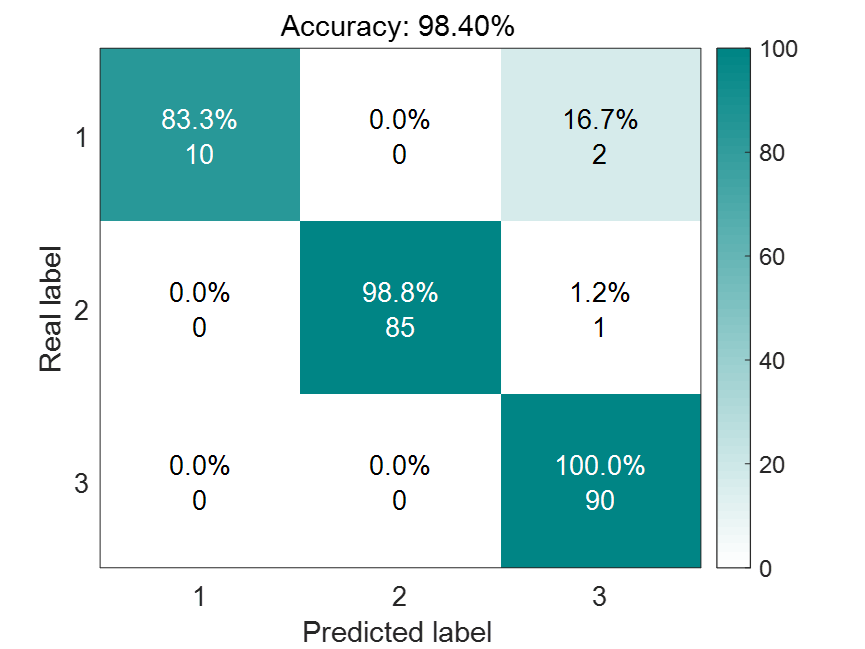
SCNGO-BP分类结果：

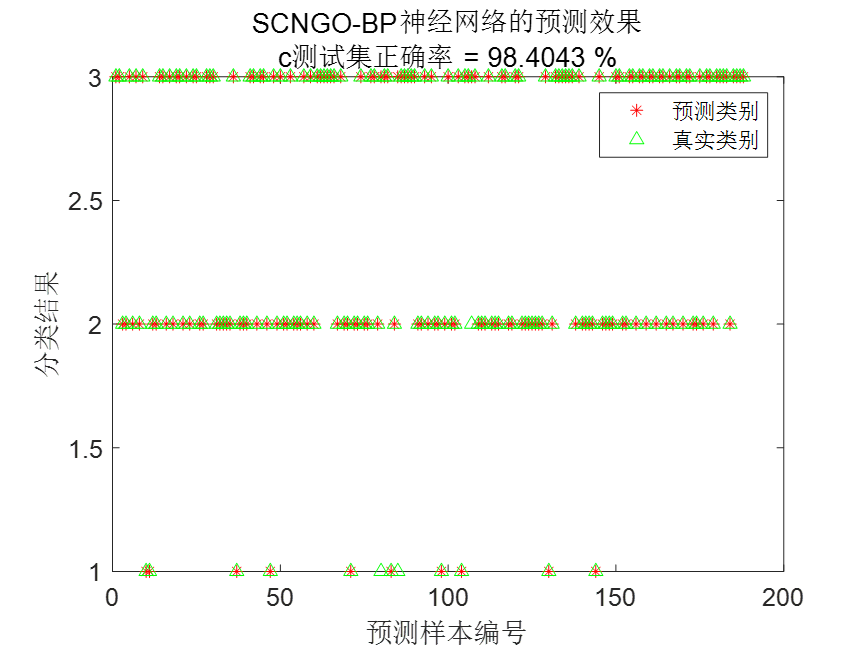
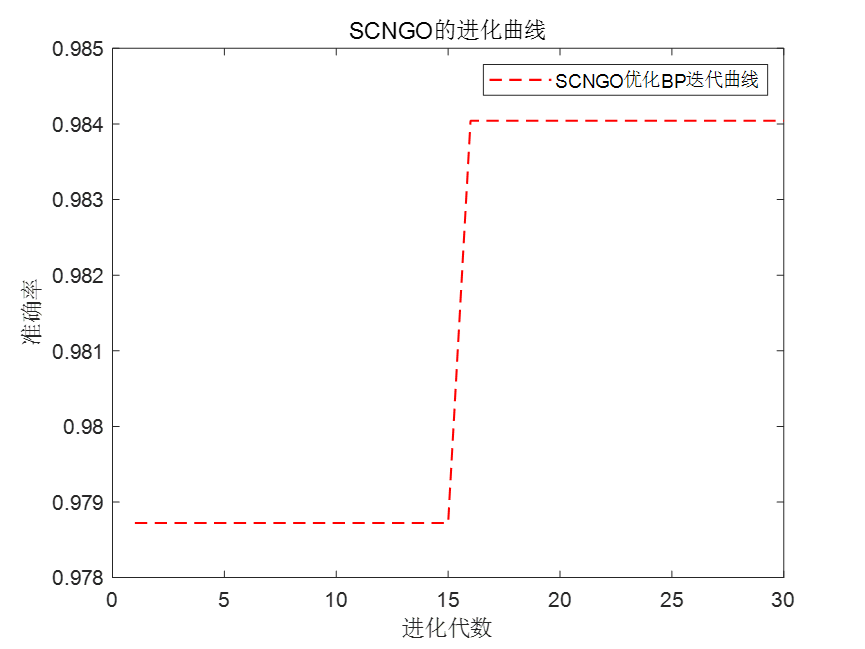
03 代码展示

%% 初始化
clear
close all
clc
warning off
addpath(genpath(pwd));
% rng(0)
load Balancescale.mat 
data = Balancescale;
data=data(randperm(size(data,1)),:);    %此行代码用于打乱原始样本，使训练集测试集随机被抽取，有助于更新预测结果。
input=data(:,2:end);
output1 =data(:,1);
for i=1:size(data,1)
    switch output1(i)
        case 1
            output(i,1)=1;
        case 2
            output(i,2)=1;
        case 3
            output(i,3)=1;
        case 4
            output(i,4)=1;
        case 5
            output(i,5)=1;
        case 6
            output(i,6)=1;
        case 7
            output(i,7)=1;
    end
end
%% 划分训练集和测试集
m=fix(size(data,1)*0.7);    %训练的样本数目
%训练集
input_train=input(1:m,:)';
output_train=output(1:m,:)';
% 测试集
input_test=input(m+1:end,:)';
output_test=output(m+1:end,:)';


%% 数据归一化
[inputn,inputps]=mapminmax(input_train,0,1);
inputn_test=mapminmax('apply',input_test,inputps);
dam = fix(size(inputn,2)*0.3);%选30%的训练集作为验证集
idx = randperm(size(inputn,2),dam);
XValidation = inputn(:,idx);
inputn(:,idx) = [];
YValidation = output_train(:,idx);
output_train(:,idx) = [];


%% 获取输入层节点、输出层节点个数
inputnum=size(input_train,1);
outputnum=size(output_train,1);
disp('/')
disp('神经网络结构...')
disp(['输入层的节点数为：',num2str(inputnum)])
disp(['输出层的节点数为：',num2str(outputnum)])
disp(' ')
disp('隐含层节点的确定过程...')


%确定隐含层节点个数
%采用经验公式hiddennum=sqrt(m+n)+a，m为输入层节点个数，n为输出层节点个数，a一般取为1-10之间的整数
acc = 0;
for hiddennum=fix(sqrt(inputnum+outputnum))+1:fix(sqrt(inputnum+outputnum))+10
    net0=newff(inputn,output_train,hiddennum);
    % 网络参数
    net0.trainParam.epochs=1000;            % 训练次数，这里设置为1000次
    net0.trainParam.lr=0.01;                % 学习速率，这里设置为0.01
    net0.trainParam.goal=0.0001;           % 训练目标最小误差，这里设置为0.0001
    net0.trainParam.show=25;                % 显示频率，这里设置为每训练25次显示一次
    net0.trainParam.mc=0.001;                % 动量因子
    net0.trainParam.min_grad=1e-8;          % 最小性能梯度
    net0.trainParam.max_fail=6;             % 最高失败次数
    net0.trainParam.showWindow = false;
    net0.trainParam.showCommandLine = false; 
    % 网络训练
    [net0,tr]=train(net0,inputn,output_train);
    an0=sim(net0,XValidation);  %验证集的仿真结果
    predict_label=zeros(1,size(an0,2));
    for i=1:size(an0,2)
        predict_label(i)=find(an0(:,i)==max(an0(:,i)));
    end
    outputt=zeros(1,size(YValidation,2));
    for i=1:size(YValidation,2)
        outputt(i)=find(YValidation(:,i)==max(YValidation(:,i)));
    end
    accuracy=sum(outputt==predict_label)/length(outputt);   %计算预测的确率
    disp(['隐含层节点数为',num2str(hiddennum),'时，验证集的准确率为：',num2str(accuracy)])
    
    %更新最佳的隐含层节点
    if acc<accuracy
        acc=accuracy;
        hiddennum_best=hiddennum;
    end
end
disp(['最佳的隐含层节点数为：',num2str(hiddennum_best),'，验证集相应的训练集的准确率为：',num2str(acc)])


%% 构建最佳隐含层节点的BP神经网络
disp(' ')
disp('标准的BP神经网络：')
net0=newff(inputn,output_train,hiddennum_best,{'tansig','purelin'},'trainlm');% 建立模型
%网络参数配置
net0.trainParam.epochs=1000;         % 训练次数，这里设置为1000次
net0.trainParam.lr=0.01;                   % 学习速率，这里设置为0.01
net0.trainParam.goal=0.00001;                    % 训练目标最小误差，这里设置为0.0001
net0.trainParam.show=25;                % 显示频率，这里设置为每训练25次显示一次
net0.trainParam.mc=0.01;                 % 动量因子
net0.trainParam.min_grad=1e-6;       % 最小性能梯度
net0.trainParam.max_fail=6;               % 最高失败次数
% net0.trainParam.showWindow = false;
% net0.trainParam.showCommandLine = false;            %隐藏仿真界面
%开始训练
net0=train(net0,inputn,output_train);


%预测
an0=sim(net0,inputn_test); %用训练好的模型进行仿真
predict_label=zeros(1,size(an0,2));
    for i=1:size(an0,2)
        predict_label(i)=find(an0(:,i)==max(an0(:,i)));
    end
    outputt=zeros(1,size(output_test,2));
    for i=1:size(output_test,2)
        outputt(i)=find(output_test(:,i)==max(output_test(:,i)));
    end
    accuracy=sum(outputt==predict_label)/length(outputt);   %计算预测的确率  
    disp(['准确率为：',num2str(accuracy)])
%% 标准BP神经网络作图
% 画方框图
figure
confMat = confusionmat(outputt,predict_label);  %output_test是真实值标签
zjyanseplotConfMat(confMat.');  
xlabel('Predicted label')
ylabel('Real label')
% 作图
figure
scatter(1:length(predict_label),predict_label,'r*')
hold on
scatter(1:length(predict_label),outputt,'g^')
legend('预测类别','真实类别','NorthWest')
title({'BP神经网络的预测效果',['测试集正确率 = ',num2str(accuracy*100),' %']})
xlabel('预测样本编号')
ylabel('分类结果')
box on
set(gca,'fontsize',12)

代码中注释非常详细，有对神经网络构建的注释，有对SCNGO-BP代码的注释，简单易懂。

代码附带UCI常用的数据集及其解释。大家可以自行尝试别的数据进行分类。附带SCNGO在CEC2005函数的测试代码。

完整代码获取方式，后台回复关键词。关键词 :

SCNGOBP