数据结构中的二叉树

一、二叉树的基本概念

二叉树是一种重要的数据结构，它是每个节点最多有两个子节点的树结构。在二叉树中，每个节点都可以有左子节点和右子节点，也可以没有子节点。

二、二叉树的特点

每个节点最多有两个子节点，分别是左子节点和右子节点。
二叉树的子树也是二叉树，即左子树和右子树都是二叉树。
二叉树可以为空，即没有任何节点。
第k层上的节点个数最多为2^(k-1)个
深度为k的二叉树最多有2^k -1个节点
二叉树的高度：二叉树的高度是指从根节点到最深层的最长路径的长度。对于有n个节点的二叉树，其高度不会超过n，即h <= n。对于平衡二叉树，其高度为O(log n)，使得查找和插入等操作具有较高的效率。

三、二叉树的分类

二叉树可以根据节点的子节点个数进行分类，常见的二叉树包括：

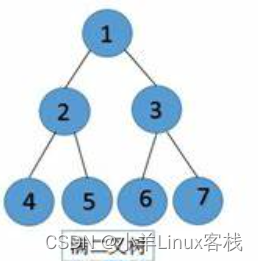
满二叉树：除了叶节点外，每个节点都有两个子节点，并且所有叶节点都在同一层上。
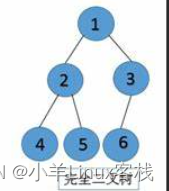
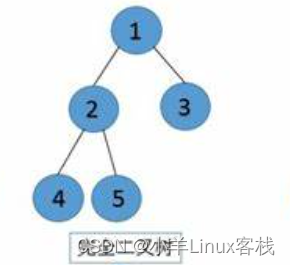
完全二叉树：除了最后一层外，其他层的节点数都达到最大值，最后一层的节点依次从左到右排列。(只有最下面两层有度数小于2的节点，且最下面一层的叶节点集中在最左边的若干位置上)
平衡二叉树：左右子树的高度差不超过1的二叉树，保持树的平衡，以提高查找性能。

四、二叉树的存储结构

二叉树的存储结构有两种常见的方式：顺序存储和链式存储。

(一)顺序存储

顺序存储是使用数组来表示二叉树，按照层次顺序将二叉树的节点存储在数组中。假设二叉树的根节点存储在数组索引为0的位置，那么第i个节点的左子节点存储在索引为2i+1的位置，右子节点存储在索引为2i+2的位置。如果节点为空，用特定的值（如NULL）表示。

// 二叉树的顺序存储示例
#define MAX_SIZE 100
int tree[MAX_SIZE];

// 初始化树
void initTree() {
    for (int i = 0; i < MAX_SIZE; i++) {
        tree[i] = NULL;
    }
}

// 添加节点
void addNode(int value, int index) {
    tree[index] = value;
}

// 获取左子节点
int getLeftChild(int index) {
    return tree[2 * index + 1];
}

// 获取右子节点
int getRightChild(int index) {
    return tree[2 * index + 2];
}

(二)链式存储

链式存储是使用指针来表示二叉树，每个节点包含数据和指向左右子节点的指针。通过指针，可以将各个节点串联起来，形成一棵完整的二叉树。

// 二叉树的链式存储示例
typedef struct TreeNode {
    int data;
    struct TreeNode* left;
    struct TreeNode* right;
} TreeNode;

// 创建节点
TreeNode* createNode(int value) {
    TreeNode* newNode = (TreeNode*)malloc(sizeof(TreeNode));
    newNode->data = value;
    newNode->left = NULL;
    newNode->right = NULL;
    return newNode;
}

// 添加节点
void addNode(TreeNode* parent, TreeNode* leftChild, TreeNode* rightChild) {
    parent->left = leftChild;
    parent->right = rightChild;
}