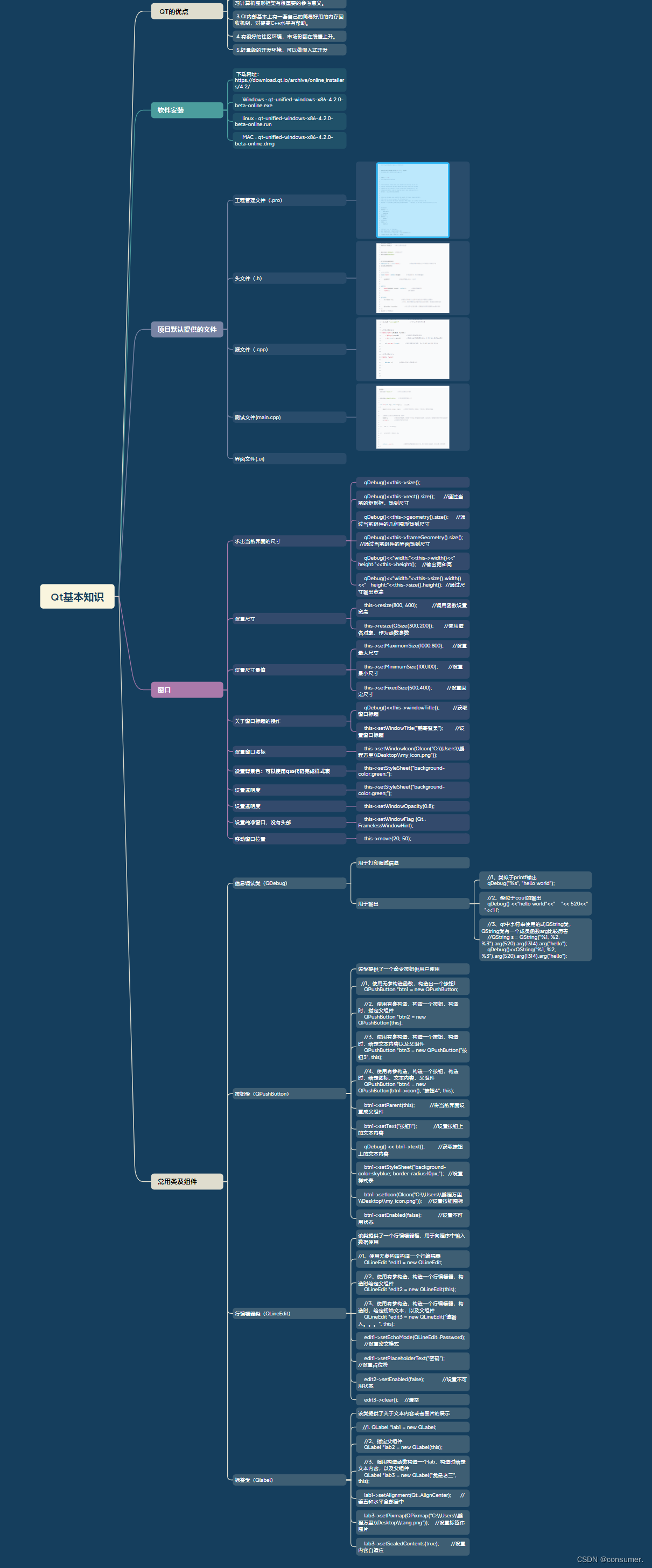
两个变量的二元分布可视化也很有用。在 Seaborn中最简单的方法是使用 jointplot()函数,该函数可以创建一个多面板图形,比如散点图、二维直方图、核密度估计等,以显示两个变量之间的双变量关系及每个变量在单坐标轴上的单变量分布。
jointplot()函数的语法格式如下。
seaborn.jointplot(x, y, data=None,
kind='scatter', stat_func=None, color=None,
ratio=5, space=0.2, dropna=True)
上述函数中常用参数的含义如下:
(1) kind:表示绘制图形的类型。
(2) stat_func:用于计算有关关系的统计量并标注图。
(3) color:表示绘图元素的颜色。
(4) size:用于设置图的大小(正方形)。
(5) ratio:表示中心图与侧边图的比例。该参数的值越大,则中心图的占比会越大。
(6) space:用于设置中心图与侧边图的间隔大小。
下面以散点图、二维直方图、核密度估计曲线为例,为大家介绍如何使用 Seaborn绘制这些图形。
1.绘制散点图
调用 seaborn.jointplot()函数绘制散点图的示例如下。
import numpy as np
import pandas as pd
import结果如下图所示。 seaborn as sns
# 创建DataFrame对象
dataframe_obj = pd.DataFrame({"x": np.random.randn(500),"y": np.random.randn(500)})
# 绘制散布图
sns.jointplot(x="x", y="y", data=dataframe_obj)
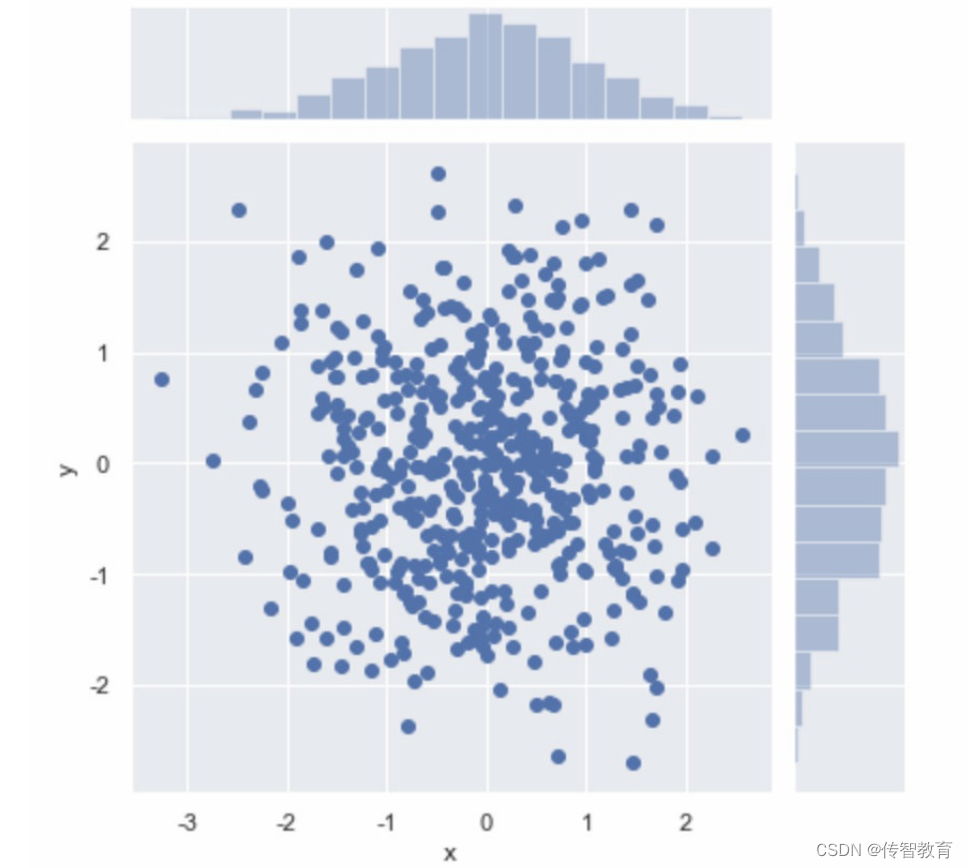
上述示例中,首先创建了一个 DataFrame对象 dataframe_obj作为散点图的数据,其中x轴和y轴的数据均为500个随机数,接着调用 jointplot0函数绘制一个散点图,散点图x轴的名称为“x”,y轴的名称为“y”。
运行结果如图所示。
2.绘制二维直方图
二维直方图类似于“六边形”图,主要是因为它显示了落在六角形区域内的观察值的计数,适用于较大的数据集。当调用 jointplot()函数时,只
要传入kind=“hex”,就可以绘制二维直方图,具体示例代码如下。
# 绘制二维直方图
sns.jointplot(x="x", y="y", data=dataframe_obj, kind="hex")
运行结果如图所示。
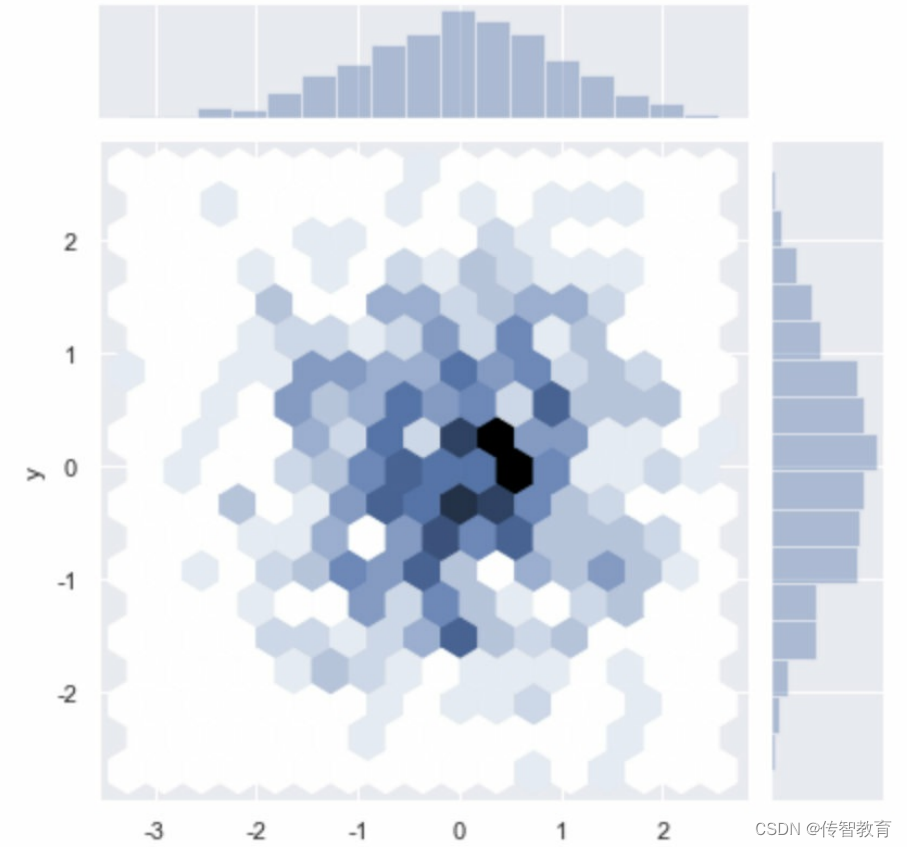
从六边形颜色的深浅,可以观察到数据密集的程度,另外,图形的上方和右侧仍然给出了直方图。注意,在绘制二维直方图时,最好使用白色背景。
3.绘制核密度估计图形
利用核密度估计同样可以查看二元分布,其用等高线图来表示。当调用jointplot()函数时只要传入ind=“kde”,就可以绘制核密度估计图形,具体示例代码如下。
sns.jointplot(x="x", y="y", data=dataframe_obj, kind="kde")
上述示例中,绘制了核密度的等高线图,另外,在图形的上方和右侧给出了核密度曲线图。运行结果如图所示。
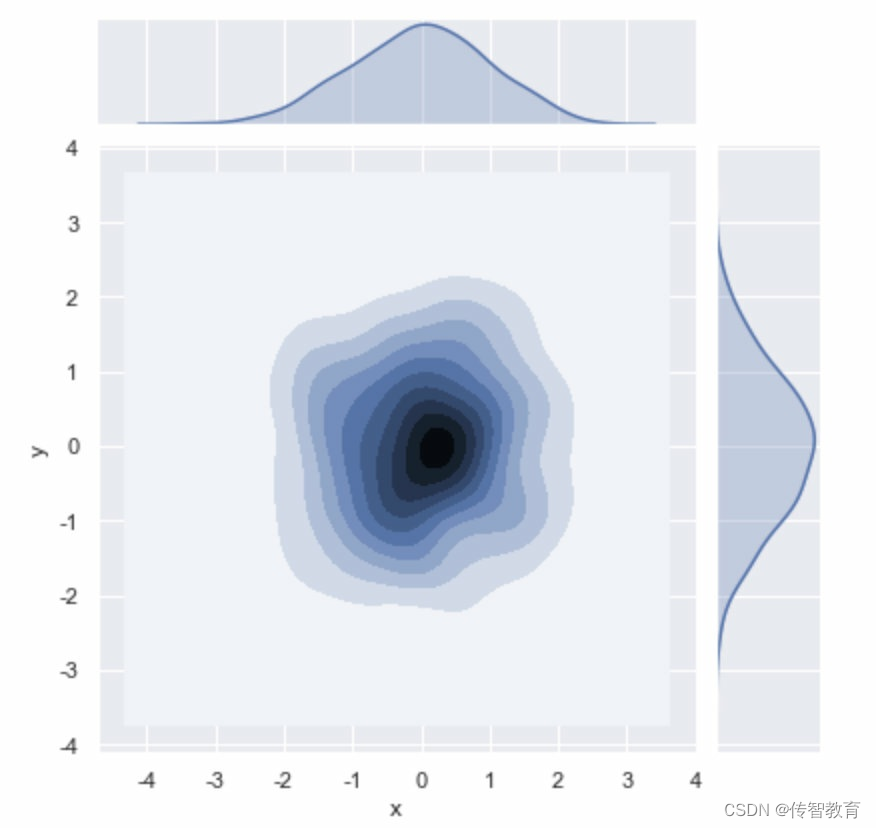
通过观等高线的颜色深浅,可以看出哪个范围的数值分布的最多,哪个范围的数值分布的最少。
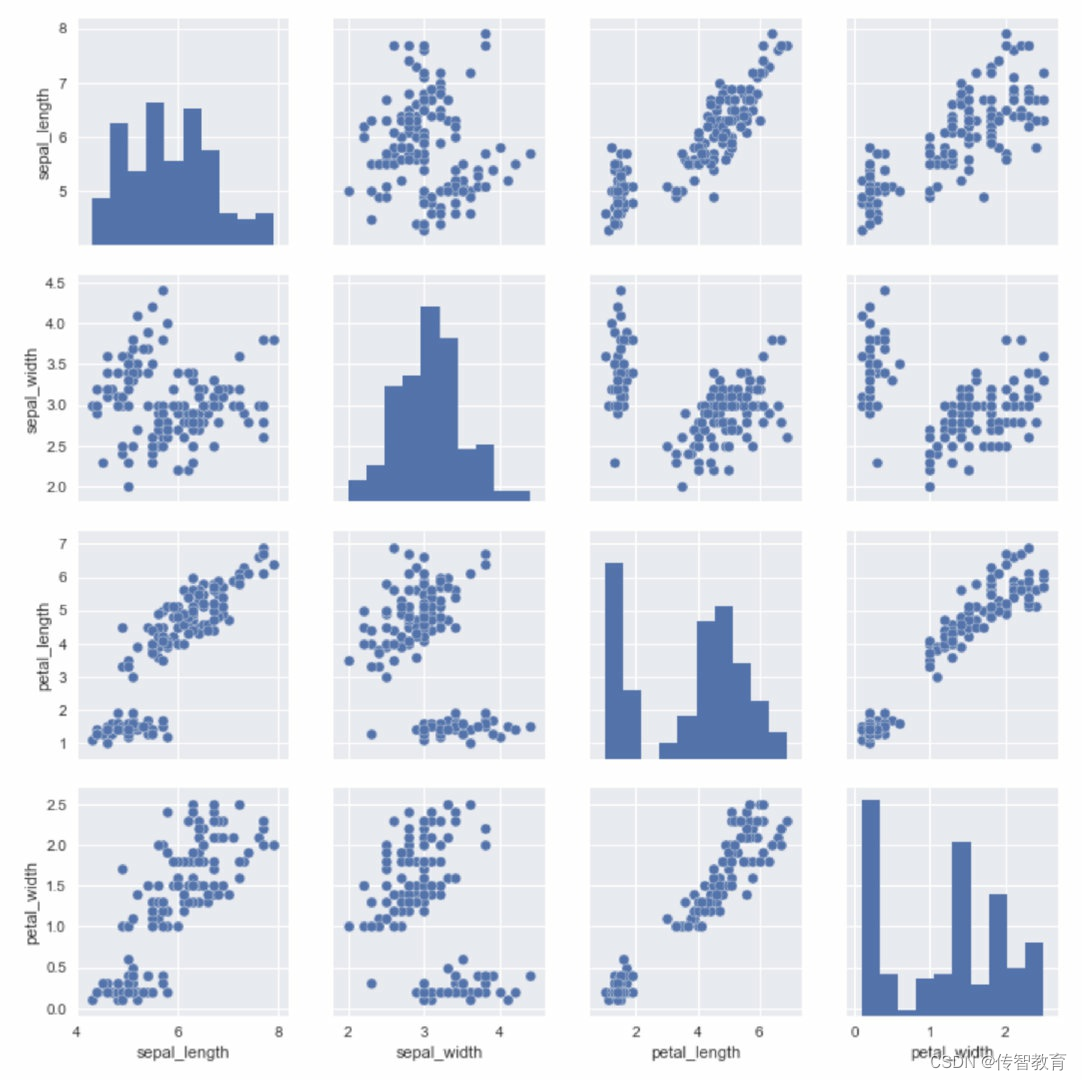
4.绘制成对的双变量分布
要想在数据集中绘制多个成对的双变量分布,则可以使用pairplot()函数实现,该函数会创建一个坐标轴矩阵,并且显示Datafram对象中每对变量的关系。另外,pairplot()函数也可以绘制每个变量在对角轴上的单变量分布。
接下来,通过sns.pairplot()函数绘制数据集变量间关系的图形,示例代码如下:
#加载seaborn中的数据集
dataset=sns.load_dataset("iris")
dataset.head()
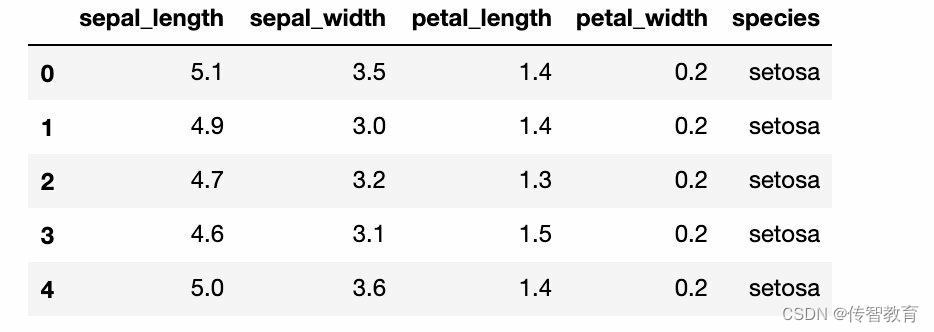
上述示例中,通过load_dataset0函数加载了seaborn中内置的数据集,根据iris数据集绘制多个双变量分布。
#绘制多个成对的双变量分布
sns.pairplot(dataset)
结果如下图所示。