A - First ABCA - First ABC

题目大意

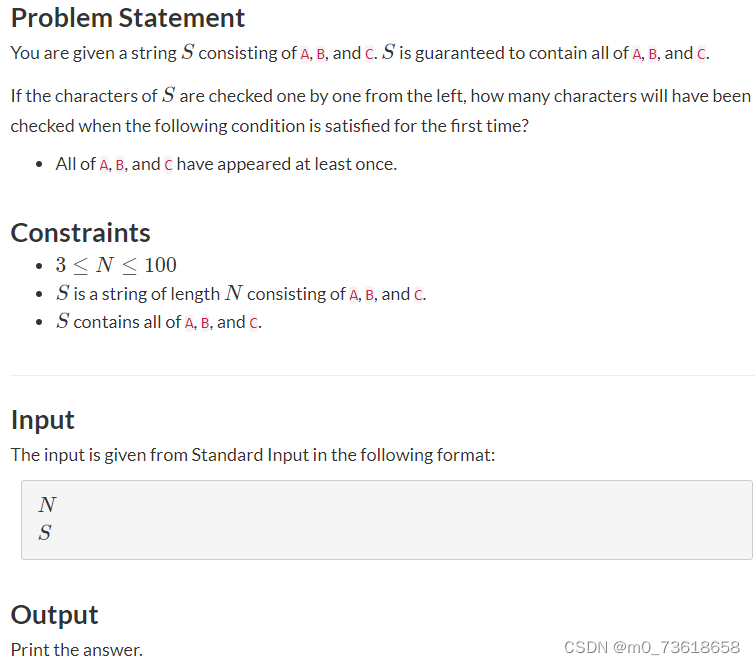
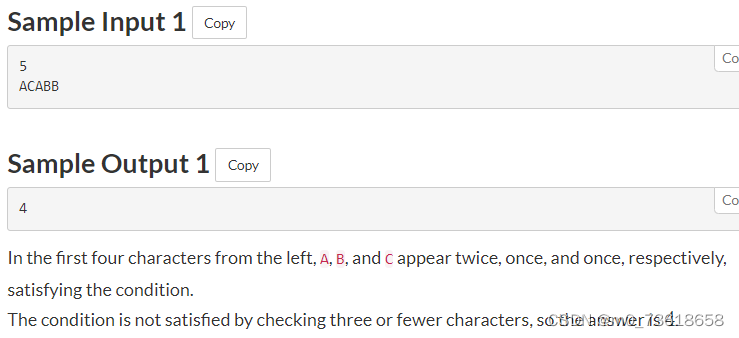
需要找到满足条件的最小字符数量。条件是字符串S中出现了A、B和C各至少一次。

思路分析

可以使用一个unordered_set来存储已经出现的字符，每次遍历字符串S时，将字符加入集合中。当集合中的元素数量达到3时，即表示A、B和C都已经出现过，此时记录当前位置i+1，并且退出循环。

时间复杂度

O(N)

AC代码

#include<bits/stdc++.h>
using namespace std;
int main()
{
    int n;
    cin>>n;
    string s;
    cin>>s;
    unordered_set<char> ch; // 用于存储已经出现的字符
    int cnt = 0; // 计数器，记录满足条件的字符数量
    for(int i=0;i<n;i++)
    {
        ch.insert(s[i]); // 将当前字符加入集合ch中
        if(ch.size()==3){ // 检查集合ch的大小是否等于3
            cnt=i+1; // 记录当前位置i+1到计数器cnt中
            break; // 退出循环
        }
    }
    cout<<cnt<<endl; // 输出计数器cnt的值作为结果
    return 0;
}

B - Vacation TogetherB - Vacation Together

题目大意

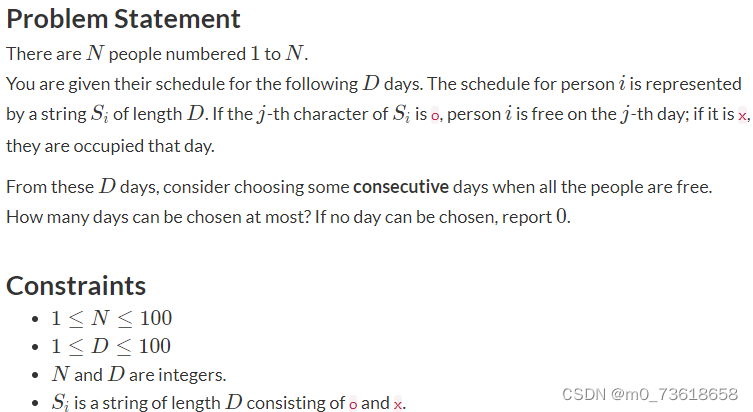
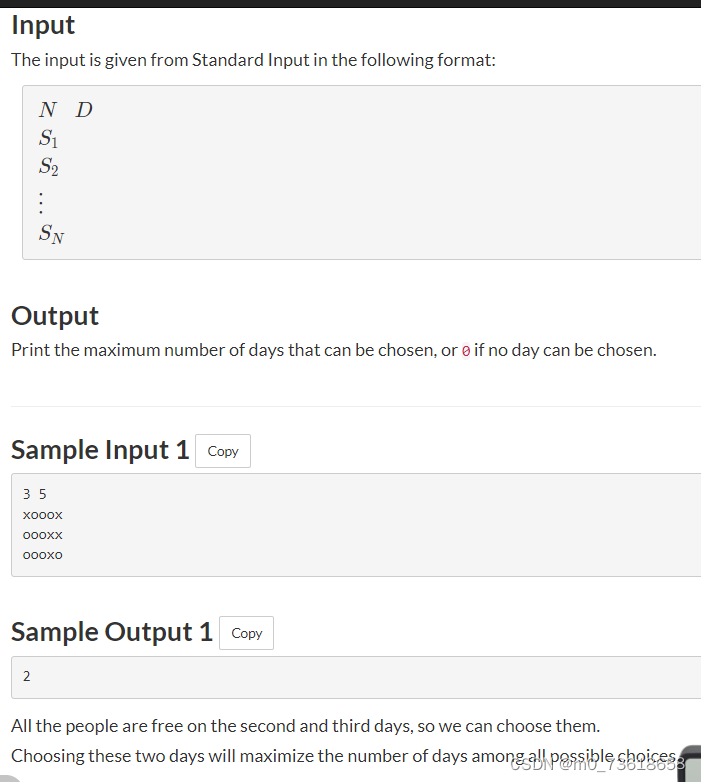
题目要求找出一段连续的天数，使得所有人都有空。给定N个人的日程安排，用长度为D的字符串Si表示第i个人的日程安排。如果Si的第j个字符是o，则表示第i个人在第j天有空；如果是x，则表示占用。
需要找出最多能选择的连续天数。如果没有可以选择的天数，则输出0。

思路分析

通过遍历每一天，逐步累加连续空闲的天数，并记录下最大的天数。当遇到有人占用的天数时，可以重新开始计数。这样做可以找到最长的连续空闲天数。

时间复杂度

O(D*N)

AC代码

#include<bits/stdc++.h>
using namespace std;

int main() {
    int n, d;
    cin >> n >> d;

    vector<string> sc(n);
    for (int i = 0; i < n; i++) {
        cin >> sc[i];
    }

    int ma = 0, cu = 0;
    for (int i = 0; i < d; i++) {
        bool fr = true;
        for (int j = 0; j < n; j++) {
            if (sc[j][i] == 'x') {
                fr = false;
                break;
            }
        }
        if (fr) {
            cu++;
            ma = max(ma, cu);
        } else {
            cu = 0;
        }
    }

    cout << ma << endl;
    return 0;
}

C - Find it! C - Find it!

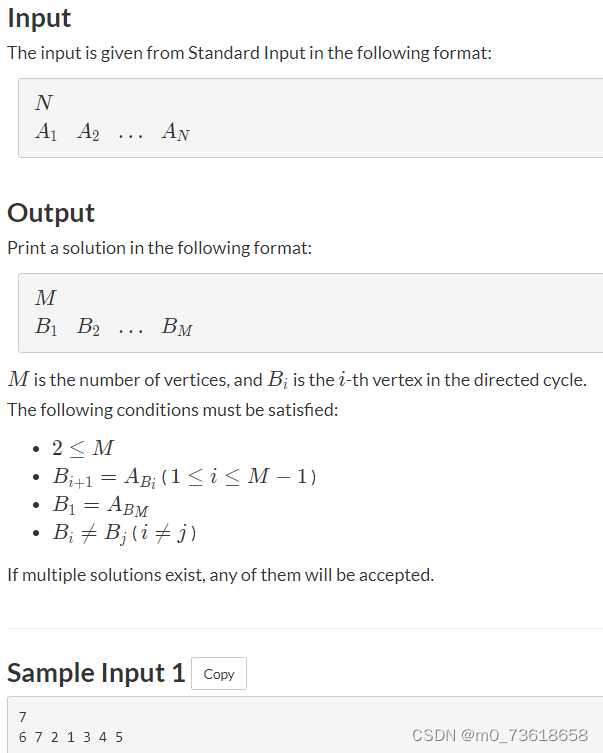
题目大意

题目要求在给定的有向图中找到一个无重复顶点的有向环。图有N个顶点和N条边。第i条边从顶点i指向顶点Ai.

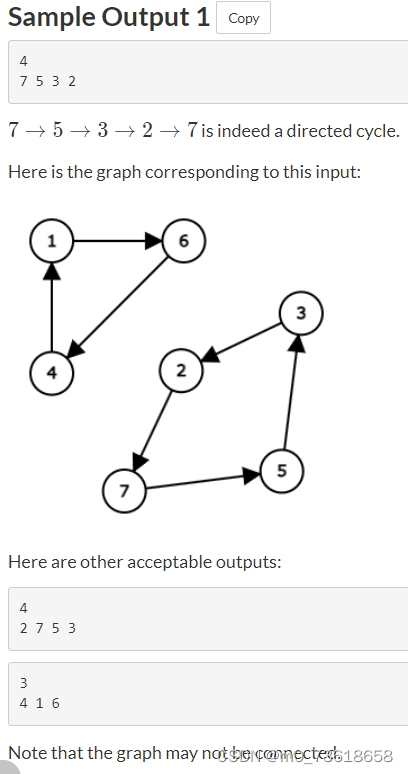
思路分析

使用DFS，可以从任意一个顶点开始，沿着边进行探索，直到找到一个已经访问过的顶点为止，从而找到一个可能的有向环。然后，再次进行DFS，直到回到起点，以获得无重复顶点的有向环。

时间复杂度

O(N+M)

AC代码

#include <bits/stdc++.h>

using namespace std;

vector<int> g;              // 存储图的连接关系
vector<int> visited;        // 记录顶点是否已访问
vector<int> v;              // 存储有向环中的顶点
int aux = 0, c = 0;         // 辅助变量

// 第一次DFS，找到有向环的起点和终点
void dfs(int i) {
    visited[i]++;

    if (visited[g[i]]) {
        aux = g[i];
    }
    else {
        dfs(g[i]);
    }
}

// 第二次DFS，找到无重复顶点的有向环
void dfs2(int i) {
    c++;
    visited[i]++;
    v.push_back(i);

    if (visited[g[i]] == 1)
        dfs2(g[i]);
}

int main() {
    int n;
    cin >> n;

    g = vector<int>(n);
    visited = vector<int>(n);

    for (int i = 1; i <= n; i++) {
        cin >> g[i];
    }

    dfs(1);     // 从任意一个未访问过的顶点开始进行DFS

    dfs2(aux);  // 从有向环的起点开始再次进行DFS

    cout << c << "\n";
    for (int i = 0; i < c; i++) {
        cout << v[i] << " ";
    }
}