A - 10yen StampA - 10yen Stamp
题目大意
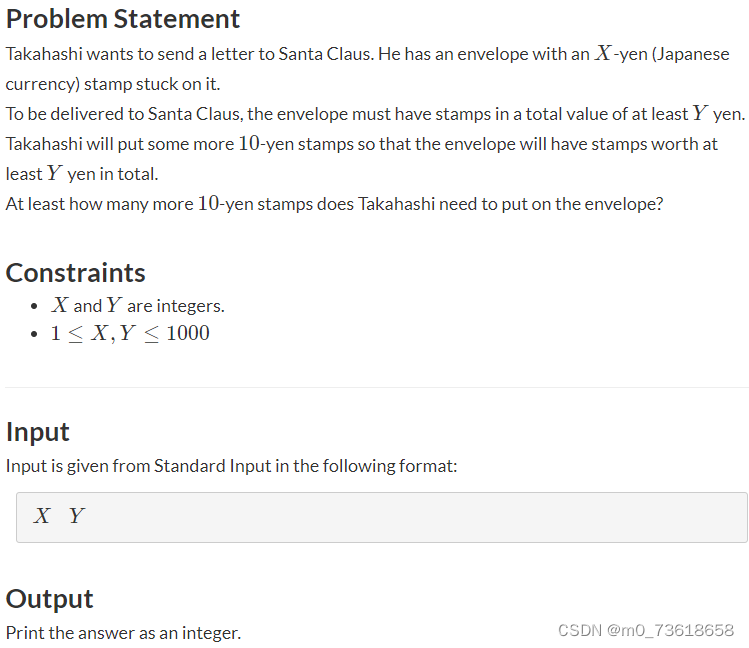
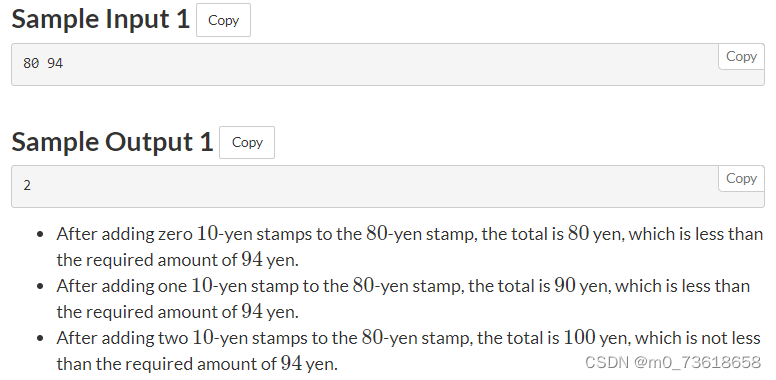
Takahashi已有X日元邮票,计算出Takahashi至少需要再贴多少个10日元的邮票才能使得信封上的邮票总价值达到Y日元。
思路分析
我们只需要计算Y - X,即Y日元减去X日元的差值。如果该差值大于等于0,则说明已经满足条件,不需要再贴任何10日元的邮票;如果该差值小于0,则需要将其除以10并向上取整,得到所需的10日元邮票数量。
知识点
- 向上取整:通过将(a+b-1)除以b的方式实现。
时间复杂度
O(1)
AC代码
向上取整做法:
#include<bits/stdc++.h>
using namespace std;
int ceil(int a,int b){return (a+b-1)/b;}
int main(){
int x,y;
cin >> x >> y;
if(x>=y){cout << "0\n";return 0;}
cout << ceil(y-x,10) << '\n';
return 0;
}
普通做法
#include<bits/stdc++.h>
using namespace std;
int main()
{
int x,y;
cin>>x>>y;
if(y<x)cout<<0<<endl;
else{
if((y-x)%10==0) cout<<(y-x)/10;
else cout<<(y-x)/10+1;
}
return 0;
}
B - A Reverse B - A Reverse
题目大意
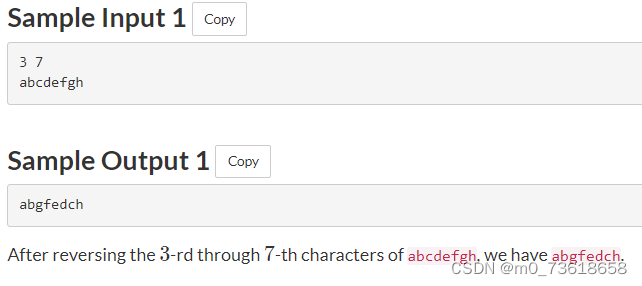
题目要求对给定的字符串S中的第L个字符到第R个字符进行反转,并输出结果。
思路分析
可以使用双指针的方法来实现字符串的反转。
- 通过使用双指针的方法,可以同时从字符串的两端向中间遍历并交换字符,实现字符串的反转。这样可以避免直接修改原始字符串,而是通过交换字符的方式得到反转后的结果。
时间复杂度
O(N/2)
AC代码
#include<bits/stdc++.h>
using namespace std;
int main(){
int l, r;
string s;
cin >> l >> r >> s;
l--; r--; // 将l和r减1,使得索引从0开始
int p = l, q = r;
while(p < q){
swap(s[p], s[q]); // 交换第p个和第q个字符
p++; q--; // 移动指针
}
cout << s << '\n';
return 0;
}
C - Product C - Product
题目大意
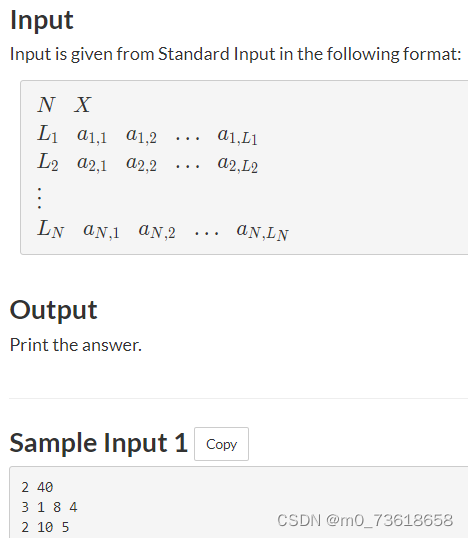
有N个袋子,每个袋子里都装着一些球,每个球上都写有一个正整数。我们要从每个袋子中选择一个球,使得所选球的数字乘积等于给定的X。询问有多少种不同的选择方式。
思路分析
使用DFS,该问题属于组合型问题,需要穷举所有可能的组合。DFS能够按照一定的规则进行深入搜索,找出所有符合条件的组合。
定义一个DFS函数,用于进行深度优先搜索。其中pos表示当前处理的袋子索引,seki表示当前累积的乘积。当pos等于N时,表示已经处理完所有袋子,判断seki和X是否相等,如果相等则计数器加一。否则,继续递归调用DFS函数,处理下一个袋子。
时间复杂度
O(L^N)
AC代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll ans = 0;
ll n,x;
vector<vector<ll>>a;
void dfs(ll pos, ll seki) {
if (pos == n) {
if (seki == x) ans++;
return;
}
for (ll c : a[pos]) {
if (seki > x / c) continue;
dfs(pos + 1, seki * c);
}
}
int main() {
cin >> n >> x;
a.resize(n);
for (ll i = 0; i < n; i++) {
ll L;
cin >> L;
a[i].resize(L);
for (ll j = 0; j < L; j++) {
cin >> a[i][j];
}
}
dfs(0, 1);
cout << ans << endl;
return 0;
}